data-mining

3. Dimensionality reduction

3.1 Introduzione

Molte fonti di dati possono essere viste come matrici di grandi dimensioni (web, social network [matrici di adiacenza], sistemi di raccomandazione [matrice di utilità]). Una matrice può essere riassunta da matrici di dimensione minore, con cui è più efficiente effettuare operazioni. Queste vengono ricavate con metodi di riduzione della dimensionalità. Si effettua riduzione della dimensionalità poiché alcune feature possono risultare irrilevanti, poiché vi è necessità di visualizzare i dati ad alta dimensionalità o poiché la dimensione intrinseca può essere inferiore al numero di feature.

3.1.1 Unsupervised feature selection

Nella feature selection supervisionata vengono selezionate le feature più interessanti rispetto ad una certa etichetta di classe. La dimensionality reduction può essere considerata una feature selection non supervisionata, poiché non si basa su etichette di classe, anche se le feature non vengono selezionate, bensì vengono definite in funzione di quelle originali.

3.1.2 Visualizzazione della riduzione

Supponiamo di avere dei punti distribuiti in uno spazio di dimensione $D$. Può capitare che i punti cadano tutti vicini (o direttamente su) uno spazio a dimensione minore $d$. In questo caso gli assi del sottospazio $d$ sono l’effettiva rappresentazione dei dati.

3.1.3 Richiami di algebra lineare

• Il rango di una matrice $A$ è un numero intero non negativo associato alla matrice $A$. Ne indica il numero di righe (o colonne) linearmente indipendenti, ovvero non ricavabili attraverso combinazioni lineari di altre righe (o colonne).
• Si dice base di uno spazio vettoriale un insieme di vettori grazie ai quali possiamo ricostruire in modo unico tutti i vettori dello spazio mediante combinazioni lineari. Disponendo di una base di uno spazio vettoriale conosciamo quindi, automaticamente, l'intero spazio vettoriale.
• Si dicono coordinate (o componenti) di un vettore rispetto a una base gli scalari mediante cui il vettore si esprime come combinazione lineare dei vettori della base. Equivalentemente, fissata una base di uno spazio vettoriale, le coordinate di un vettore rispetto alla base scelta sono i coefficienti della combinazione lineare con cui si esprime il vettore in termini degli elementi della base.
• Sia $M$ una matrice quadrata. Sia $\lambda$ una costante ed $\bar{e}$ un vettore colonna non-zero con lo stesso numero di righe di $M$. Diciamo che $\lambda$ è un autovalore di $M$ ed $\bar{e}$ è il suo corrispondente autovettore di $M$ se $M\bar{e}=\lambda \bar{e}$. La coppia $(\lambda ,\bar{e})$ prende il nome di autocoppia.
• Se $\bar{e}$ è un autovettore di $M$ con autovalore $\lambda$ e $c$ è una qualsiasi costante, allora anche $c\cdot \bar{e}$ è un autovettore di $M$ con lo stesso autovalore $\lambda$. Moltiplicare il vettore per una costante cambia il suo modulo ma non la sua direzione. Per evitare ambiguità assumeremo che ogni autovettore sia un vettore unitario (unit vector), ovvero di modulo 1.
• Sia $M$ una matrice quadrata con autovalori ${\lambda }_1,\dots ,{\lambda }_n$ e corrispondenti autovettori ${\bar{e}}_1,\dots ,{\bar{e}}_n$. Se succede che $|{\lambda }_1|>\cdots >|{\lambda }_n|$ allora chiameremo ${\lambda }_1$ autovalore principale

3.1.4 Esempio pratico

Supponiamo di avere in input la seguente matrice A $$A=\left[\begin{array}{ccccc}1& 1& 1& 0& 0\\ 2& 2& 2& 0& 0\\ 1& 1& 1& 0& 0\\ 5& 5& 5& 0& 0\\ 0& 0& 0& 2& 2\\ 0& 0& 0& 3& 3\\ 0& 0& 0& 1& 1\end{array}\right]$$ La matrice $A$ è bidimensionale, questo poiché è rappresentabile a partire dalla base $$[1,1,1,0,0],[0,0,0,1,1]$$ Se si volesse ricostruire la quarta riga, sarebbe possibile sfruttare una combinazione lineare dei vettori (generatori) della base: $$5\cdot [1,1,1,0,0]+0\cdot [0,0,0,1,1]=[5,5,5,0,0]$$ Il rango della matrice è quindi l'effettiva dimensione (intrinseca) della matrice. Facciamo un altro esempio: $$A=\left[\begin{array}{ccc}1& 2& 1\\ -2& -3& 1\\ 3& 5& 0\end{array}\right]$$ La terza riga è ottenibile dalla differenza tra la prima e la seconda riga, per cui non è linearmente indipendente. Questo vuol dire che il rango è minore di 3. Determinato il rango $\rho (A)=2$, indichiamo una nuova base per la matrice: $$[1,2,1],[-2,-3,1]$$ Ed otteniamo delle nuove coordinate per le tre righe: $$[1,0],[0,1],[1,-1]$$ I vettori della base sono gli assi di rappresentazione dei dati, per cui possiamo rappresentare i dati come coefficienti di tali vettori e lavorare su dimensioni minori (2 anziché 3). Per ritornare da coordinate $(a,b)$ alla base di partenza è sufficiente calcolare la combinazione lineare $a\cdot [1,2,1]+b\cdot [-2,-3,1]$.

3.1.5 Idea principale

L'obiettivo della dimensionality reduction è proprio quello di identificare gli assi dei dati. Molto spesso i dati non giacciono esattamente su una dimensione minore, per cui è necessario ammettere un margine di errore. Dato un insieme di punti in uno spazio $d$-dimensionale, l'idea principale è quella di proiettare i dati in uno spazio con meno dimensioni preservando quanta più informazione possibile. Scegliamo la proiezione che minimizza il quadrato dell'errore quando ricostruiamo i dati originali.

3.2 Calcolo di autovalori ed autovettori

Nei richiami di algebra lineare abbiamo scritto che, per ogni autocoppia $(\lambda ,\bar{e})$ si ha che: $$M\bar{e}=\lambda \bar{e}$$ Possiamo riscrivere l'equazione nel seguente modo: $$(M-\lambda I)e=\bar{0}$$

Dove $I$ è una matrice identità delle stesse dimensioni di $M$. Tale equazione in forma matriciale è rappresentabile come un sistema di equazioni lineari. La matrice $(M-\lambda I)$ corrisponde alla matrice $M$ la cui diagonale è ridotta di una fattore $\lambda$. Sia $\lambda$ incognita, vogliamo trovare gli autovalori e gli autovettori della matrice $M$.

Affinché si risolva l'equazione $(M-\lambda I)e=\bar{0}$ per un vettore $\bar{e}\ne \bar{0}$, il determinante della matrice $M-\lambda I$ deve essere diverso da 0. Ciò è necessario poiché se $det(M-\lambda I)=0$ allora per il teorema di Cramer il sistema lineare ammette una sola soluzione, che è banalmente $\bar{e}=0$ (ma vogliamo una soluzione $\bar{e}\ne 0$). Sebbene il determinante di una matrice $n\times n$ abbia $n!$ termini, questo può essere calcolato in diversi modi in tempo $O(n^3)$, di seguito vedremo uno tra questi metodi.

3.2.1 Chiò pivotal condensation

Il metodo Chio pivotal condensation (condensazione pivotale) permette di calcolare il determinante di una matrice $A$ di dimensione $n\times n$ andando a dividere il determinante di una nuova matrice $B$ di dimensione $(n-1)\times (n-1)$ per il primo elemento della matrice $A$ elevato ad $n-2$: $$\det (A)=\frac{\det (B)}{a_{11}^{n-2}}$$ Ipotesi necessaria è che la diagonale della matrice $A$ sia non nulla, quindi che $a_{ii}\ne 0$. La matrice $B$ va costruita in funzione della matrice $A$. Il generico elemento $b_{ij}$ è ottenuto come segue: $$b_{ij}=a_{11}\times a_{i+1,j+1}-a_{1,j+1}\times a_{i+1,1}$$ Si applica ricorsivamente il metodo alla matrice $B$ sino a che non si arriva ad una matrice il quale determinante è trattabile con metodi diretti.

3.2.2 Risolvere l'equazione

Dato che il determinante della matrice $(M-\lambda I)$ è un polinomio di grado $n$ dove $\lambda$ è l'incognita, allora possiamo ottenere $n$ soluzioni, ovvero ottenere tutti ed $n$ gli autovalori della matrice $M$. Un valore $c$ qualsiasi tra queste $n$ soluzioni risolverà l'equazione $M\bar{e}=c\bar{e}$.

Per ogni autovalore $\lambda$ trovato, è possibile ricavare il corrispondente autovettore $\bar{e}$ risolvendo il sistema lineare di $n$ equazioni in $n$ incognite, ovvero le componenti dell'autovettore $\bar{e}$: $$(M-\lambda I)\bar{e}=\bar{0}$$ Per semplicità imponiamo che ogni autovettore sia unitario, trovando così una sola soluzione. Facciamo un esempio banale: $$M=\left[\begin{array}{cc}2& 1\\ 3& 2\end{array}\right]$$ Quindi impostiamo l'equazione: $$\left(\left[\begin{array}{cc}2& 1\\ 3& 2\end{array}\right]-\left[\begin{array}{cc}\lambda & 0\\ 0& \lambda \end{array}\right]\right)\cdot \left[\begin{array}{c}{e}_1\\ e_2\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]$$ Risolvendo la sottrazione all'interno delle parentesi otteniamo: $$(M-\lambda I)=\left[\begin{array}{cc}2-\lambda & 1\\ 3& 2-\lambda \end{array}\right]$$ Il determinante di questa matrice deve essere 0 poiché il sistema lineare abbia soluzioni: $$\det \left(\left[\begin{array}{cc}2-\lambda & 1\\ 3& 2-\lambda \end{array}\right]\right)=\left[(2-\lambda )\times (2-\lambda )\right]-(3\times 1)={\lambda }^2-4\lambda +1=0$$ Risolvendo il polinomio di grado $n=2$ troviamo i due autovalori: $${\lambda }_1=2+\sqrt{3}\text{ ; }{\lambda }_2=2-\sqrt{3}$$ Prendiamo la soluzione ${\lambda }_1$ e sostituiamola all'equazione precedente: $$\left(\left[\begin{array}{cc}2& 1\\ 3& 2\end{array}\right]-\left[\begin{array}{cc}{\lambda }_1& 0\\ 0& {\lambda }_1\end{array}\right]\right)\cdot \left[\begin{array}{c}{e}_1\\ e_2\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]$$ Ovvero: $$\{\begin{array}{l}(2-{\lambda }_1)e_1+e_2=0\\ 3e_1+(2-{\lambda }_1)e_2=0\\ \sqrt{e_1^2+e_2^2}=1\text{ (vincolo)}\end{array}$$ Risolviamo il sistema lineare ed otteniamo le componenti dell'autovettore ${\bar{e}}^{(1)}$ associato all'autovalore ${\lambda }_1$. Ripetiamo il processo con l'autovalore ${\lambda }_2$.

3.2.3 Power iteration

Nella pratica, per matrici molto grandi, la soluzione precedente non è ammissibile. Studiamo un metodo alternativo computazionalmente meno oneroso, chiamato power iteration. Sia $M$ una matrice di dimensioni $n\times n$ per la quale desideriamo calcolare le autocoppie.

Partiamo da un vettore generato casualmente ${\bar{x}}_1$ di dimensione $n$. Calcoliamo un nuovo vettore ${\bar{x}}_2$ come segue: $${\bar{x}}_2=\frac{M\cdot {\bar{x}}_1}{||M\cdot {\bar{x}}_1||}$$ dove con $||M||$ intendiamo la norma di Frobenius: $$||M||=\sqrt{\sum _{i,j}{m}_{ij}^2}$$ Osserviamo che, così facendo, il vettore ${\bar{x}}_2$ sarà normalizzato ad 1. Procediamo iterativamente calcolando il generico vettore ${\bar{x}}_i$ (per $i>1$) come segue: $${\bar{x}}_i=\frac{M\cdot {\bar{x}}_{i-1}}{||M\cdot {\bar{x}}_{i-1}||}$$ Fissato arbitrariamente un valore costante piccolo $ϵ$, l'iterazione si fermerà quando $$||x_i-x_{i+1}||\le ϵ$$ A questo punto, $x_i$ è approssimativamente l'autovettore principale di $M$. Calcoliamo l'autovalore corrispondente attraverso la formula inversa: $${\lambda }_1={{\bar{x}}_i}^T\cdot M\cdot {\bar{x}}_i$$ Utilizzando questo metodo ricaveremo la prima autocoppia principale $({\lambda }_1,{\bar{x}}_1)$ (oss. ${\lambda }_1$ è l'autovalore più grande). Per calcolare le rimanenti autocoppie è necessario enunciare il seguente teorema.

3.2.4 Generalizzazione della Power iteration

Sia $A$ una matrice simmetrica di dimensione $n\times n$ con $({\lambda }_1,\dots ,{\lambda }_n)$ autovalori e $({\bar{v}}_1,\dots ,{\bar{v}}_n)$ autovettori. Supponiamo di aver calcolato l'autocoppia principale $({\lambda }_1,{\bar{v}}_1)$ attraverso la power iteration. Per trovare la seconda autocoppia, creiamo una nuova matrice: $$B=A-{\lambda }_1{\bar{v}}_1{\bar{v}}_1^T$$ Applicare la power iteration alla matrice $B$ restituirà l'autocoppia principale $({\lambda }^{\ast },{\bar{v}}^{\ast })$ della matrice $B$, ovvero l'autocoppia con autovalore più grande. Tale autocoppia corrisponde alla seconda autocoppia della matrice $A$ di partenza. Intuitivamente, quello che abbiamo fatto è stato rimuovere l'influenza dell'autovettore principale ${\bar{v}}_1$ impostando il corrispondente autovalore principale ${\lambda }_1$ a zero. Ciò viene giustificato dalle seguenti osservazioni:

• ${\bar{v}}_1$ è ancora un autovettore di $B$ ed il suo autovalore corrispondente è $0$.
• se $(\lambda ,{\bar{v}}_{\lambda })$ è una autocoppia (non principale) di una matrice simmetrica $A$ allora sarà una autocoppia di $B$.

È possibile trovare tutte le autocoppie ripetendo iterativamente il metodo: $$B_{t+1}=B_t-{\lambda }_t{\bar{v}}_t{\bar{v}}_t^T$$

Osservazione: Se gli autovettori non sono unitari, allora non sarà possibile calcolare la matrice B con l'espressione indicata, bensì si dovrà trovare un vettore $\bar{x}$ tale che $\bar{v}\cdot \bar{x}=1$ e quindi calcolare la matrice B come segue: $$>B=A-{\lambda }_1{\bar{v}}_1{\bar{x}}^T>$$

Il professore sostiene che l'autovettore ottenuto dalla power iteration su $B$, che chiameremo ${\bar{u}}_i$ non corrisponda all'autovettore su $A$, che chiameremo ${\bar{v}}_i$, e che per calcolare l'autovettore originale bisogna applicare la seguente formula: $$>{\bar{v}}_i=({\lambda }_1-{\lambda }_i)\cdot {\bar{u}}_i+{\lambda }_1\cdot ({\bar{v}}_1^T\cdot {\bar{u}}_i)\cdot {\bar{v}}_1\text{ per }i=2,\dots ,n>$$

3.2.5 Implementazione

import numpy as np
import numpy.linalg as la 

def powi (m, max_iter = 10 ** 3):
    """ power iteration method """
    _, n = m.shape
    x = np.ones(n)
    for _ in range(max_iter):
        mx = np.dot(m, x)
        fn = la.norm(mx, 'fro')
        x = mx / fn
        x = x.A[0]
    ev = np.dot(np.dot(x.T, m), x).item(0)
    return ev, x
  

def eigenpairs(m):
    """ power iteration generalization for all eigenpairs """
    _, n = m.shape 
    b = m 
    evecs = [] 
    evals = []
    for i in range(n):
        lambdai, ei = powi(b)    
        evecs.append(ei)
        evals.append(lambdai)
        eim = np.matrix(ei)
        b = b - lambdai * eim.T.dot(eim)
    return evals, evecs 

def main():
    m = np.matrix([
            [1,3,5],
            [2,4,1],
            [6,1,9],
        ])

    eigen_values, eigen_vectors = eigenpairs(m)

    for key, val in enumerate(eigen_values):
        print(f'{key}) \t {val}')

3.2 PCA - Principal-Component Analysis

La Principal-Component Analysis (PCA) è una tecnica che prende un dataset relativo ad un insieme di tuple in uno spazio ad alta dimensione e trova le direzioni (assi) lungo il quale le tuple si allineano meglio. Trattiamo l'insieme di tuple come una matrice $M$ e troviamo gli autovettori di $M{M}^T$ o $M^{T}M$. La matrice di questi autovettori può essere pensata come una rotazione rigida dello spazio ad alta dimensione.

3.2.1 Esempio illustrativo

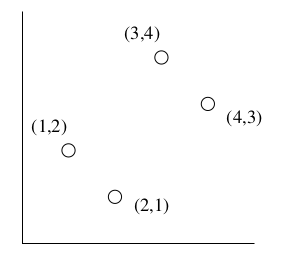
Rappresentiamo i dati nell'asse su una matrice $4\times 2$: $$M=\left[\begin{array}{cc}1& 2\\ 2& 1\\ 3& 4\\ 4& 3\end{array}\right]$$ Calcoliamo il prodotto matriciale $M^{T}M$ $$M^{T}M=\left[\begin{array}{cccc}1& 2& 3& 4\\ 2& 1& 4& 3\end{array}\right]\left[\begin{array}{cc}1& 2\\ 2& 1\\ 3& 4\\ 4& 3\end{array}\right]=\left[\begin{array}{cc}30& 28\\ 28& 30\end{array}\right]$$ Troviamo gli autovalori come fatto nel paragrafo 3.2.2 $$(30-\lambda )(30-\lambda )-28\times 28=0$$ Le cui soluzioni sono ${\lambda }_1=58$ e ${\lambda }_2=2$. Troviamo gli autovettori risolvendo l'equazione lineare per ogni autovalore: $$\text{ per }{\lambda }_1=58\text{ abbiamo }{e}_1=\left[\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right]$$

$$\text{ per }{\lambda }_2=2\text{ abbiamo }{e}_2=\left[\begin{array}{c}-\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right]$$

Costruiamo la matrice $E$ affiancando gli autovettori trovati e posizionando per primo l'autovettore principale: $$E=\left[\begin{array}{cc}\frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right]$$ Ogni matrice con vettori ortonormali (vettori unitari ed ortogonali l'un l'altro) rappresenta una rotazione e/o riflessione degli assi di uno spazio Euclideo. Se moltiplichiamo la matrice $M$ per la matrice $E$ (rotazione) otteniamo: $$ME=\left[\begin{array}{cc}1& 2\\ 2& 1\\ 3& 4\\ 4& 3\end{array}\right]\left[\begin{array}{cc}\frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right]=\left[\begin{array}{cc}\frac{3}{\sqrt{2}}& \frac{1}{\sqrt{2}}\\ \frac{3}{\sqrt{2}}& \frac{-1}{\sqrt{2}}\\ \frac{7}{\sqrt{2}}& \frac{1}{\sqrt{2}}\\ \frac{7}{\sqrt{2}}& \frac{-1}{\sqrt{2}}\end{array}\right]$$ Nel caso in esempio, la matrice rappresenta una rotazione di $45°$ in senso antiorario.

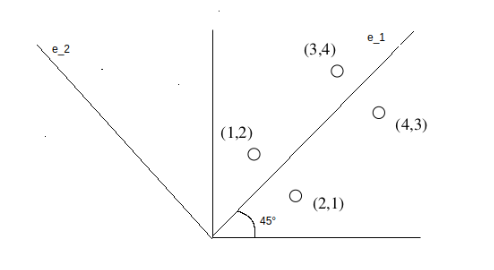
I punti mantengono le proporzioni dopo la rotazione, vediamolo graficamente:

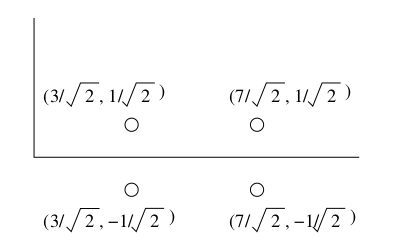
3.2.2 Ridurre la dimensionalità con PCA

$ME$ corrisponde ai punti di $M$ trasformati in uno spazio di nuove coordinate. In questo spazio, il primo asse (quello che corrisponde al più grande autovalore) è il più significativo; formalmente, la varianza di un punto lungo questo asse è la più grande. Il secondo asse corrisponde al secondo autovalore, è il successivo secondo autovalore più significativo nello stesso senso. Questo pattern si presenta per ogni autocoppia. Per trasformare $M$ in uno spazio con meno dimensioni, basta preservare le dimensioni che usano gli autovettori associati ai più alti autovalori e cancellare gli altri. Sia $E_k$ la matrice formata dalle prime $k$ colonne di $E$. Allora $M{E}_k$ è una rappresentazione di $M$ a $k$ dimensioni.

Nel nostro esempio, rimuoviamo il secondo autovettore $e_2$ dalla matrice $E$ e ricalcoliamo il prodotto $ME$: $$M{E}_1=\left[\begin{array}{cc}1& 2\\ 2& 1\\ 3& 4\\ 4& 3\end{array}\right]\left[\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right]=\left[\begin{array}{c}\frac{3}{\sqrt{2}}\\ \frac{3}{\sqrt{2}}\\ \frac{7}{\sqrt{2}}\\ \frac{7}{\sqrt{2}}\end{array}\right]$$ Tale procedura ci garantisce un errore di approssimazione minimo.

3.2.3 Pseudocodice

	
	PCA (M, k): 
		# Sia M una matrice di dati N x d, con ogni riga un vettore dei dati. 
		# Otteniamo la matrice di covarianza di M (sottraendo la media)
		Sigma <- sottraiamo la media m da ogni vettore riga
		autocoppie <- troviamo le autocoppie di Sigma 
		PC <- prendiamo i k autovettori con gli autovalori più grandi (principal components)
         # PC sarà una matrice e gli autovettori saranno posizionati in colonna
         return M * PC 
		

3.3 SVD - Singular Value Decomposition

La Singular Value Decomposition (SVD) è una tecnica che permette di ottenere una rappresentazione a basse dimensioni di una matrice ad alte dimensioni e funziona per qualsiasi matrice. Maggiore è la riduzione, minore sarà l'accuratezza della approssimazione.

3.3.1 Definizione di SVD

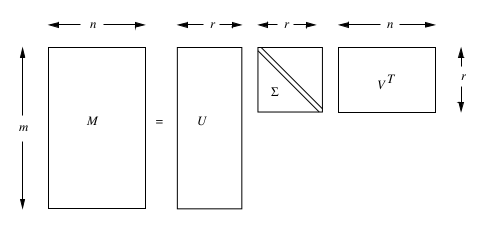
Sia $M$ una matrice $m\times n$, e sia $r$ il suo rango. Allora sarà possibile trovare le matrici $U$, $\Sigma$, e $V$ con le seguenti proprietà:

• $U$ è una column-orthonormal matrix, le cui colonne sono vettori unitari (vettori singolari di sinistra).
• $V$ è una column-orthonormal matrix, le cui colonne sono vettori unitari (vettori singolari di destra).
• $\Sigma$ è una matrice diagonale, i cui elementi (nella diagonale) sono chiamati valori singolari di $M$.

Possiamo scrivere: $$M=U\cdot \Sigma \cdot V^T$$

Per "column-orthonormal matrix" intendiamo una matrice le cui colonne sono vettori ortonormali, per cui il prodotto scalare tra due colonne distinte arbitrarie è 0. Si ha quindi che $U^{T}U=V^{T}V=I$.

Nella decomposizione si farà utilizzo della trasposta della matrice $V$, quindi $V^T$. Essendo $V$ una column-orthonormal matrix e $V^T$ la sua trasposta, allora $V^T$ sarà una row-orthonormal matrix.

3.3.2 Interpretazione della SVD

Sia $M$ una matrice di dimensione $7\times 5$ contenente nelle righe gli utenti e nelle colonne i film valutati dagli utenti. Supponiamo che i primi 3 film nelle colonne siano fantascientifici, mentre gli ultimi due siano romantici: $$M=\left[\begin{array}{ccccc}1& 1& 1& 0& 0\\ 3& 3& 3& 0& 0\\ 4& 4& 4& 0& 0\\ 5& 5& 5& 0& 0\\ 0& 0& 0& 4& 4\\ 0& 0& 0& 5& 5\\ 0& 0& 0& 2& 2\end{array}\right]$$ Le prime 4 righe sono linearmente indipendenti tra loro, così come le ultime 3 righe. Di fatto, il rango della matrice risulta essere $r=2$. Supponiamo di aver già calcolato le tre matrici $U$, $V$ e $\Sigma$, scriviamo l'equazione della decomposizione: $$(M)\left[\begin{array}{ccccc}1& 1& 1& 0& 0\\ 3& 3& 3& 0& 0\\ 4& 4& 4& 0& 0\\ 5& 5& 5& 0& 0\\ 0& 0& 0& 4& 4\\ 0& 0& 0& 5& 5\\ 0& 0& 0& 2& 2\end{array}\right]=(U)\left[\begin{array}{cc}.14& 0\\ .42& 0\\ .56& 0\\ .70& 0\\ 0& .60\\ 0& .75\\ 0& .30\end{array}\right](\Sigma )\left[\begin{array}{cc}12.4& 0\\ 0& 9.5\end{array}\right](V^T)\left[\begin{array}{ccccc}.58& .58& .58& 0& 0\\ 0& 0& 0& .71& .71\end{array}\right]$$ La chiave di lettura della decomposizione sta nell'interpretare le $r$ colonne delle matrici $U$, $V$ e $\Sigma$ come concetti nascosti nella matrice di partenza $M$. Nell'esempio i concetti sono molto chiari, le due colonne indicano i due generi principali: fantascientifico e romantico. La matrice $U$ connette gli utenti (righe di $M$) ai generi (concetti), mentre la matrice $V$ connette i film (colonne di $M$) ai concetti. Infine, la matrice $\Sigma$ indica la forza di ogni concetto.

L'esempio è particolarmente banale, nella pratica spesso la dimensione desiderata è inferiore al rango della matrice, per cui è necessario applicare alcune modifiche ed ottenere una decomposizione non esatta, ma che approssima al meglio la matrice $M$. È necessario eliminare dalla decomposizione esatta quelle colonne di $U$ e $V$ che corrispondono ai valori singolari più piccoli (concetti meno affermati) così da ottenere una buona approssimazione.

Modifichiamo leggermente la matrice d'esempio e vediamo cosa succede: $$M=\left[\begin{array}{ccccc}1& 1& 1& 0& 0\\ 3& 3& 3& 0& 0\\ 4& 4& 4& 0& 0\\ 5& 5& 5& 0& 0\\ 0& 2& 0& 4& 4\\ 0& 0& 0& 5& 5\\ 0& 1& 0& 2& 2\end{array}\right]$$ Il rango della matrice $M$ è adesso $r=3$ a causa delle modifiche: le ultime tre colonne non sono più tutte linearmente indipendenti. Tuttavia i concetti rimangono gli stessi. Vediamo cosa succede alla decomposizione: $$(U)\left[\begin{array}{ccc}.13& .02& -.01\\ .41& .07& -.03\\ .55& .09& -.04\\ .68& .11& -.05\\ .15& -.59& .65\\ .07& -.73& -.67\\ .07& -.29& .32\end{array}\right](\Sigma )\left[\begin{array}{ccc}12.4& 0& 0\\ 0& 9.5& 0\\ 0& 0& 1.3\end{array}\right](V^T)\left[\begin{array}{ccccc}.58& .59& .56& .09& .09\\ .12& -.02& .12& .69& .69\\ .40& -.80& .40& .09& .09\end{array}\right]$$ Il terzo valore singolare risulta molto piccolo rispetto ai primi due, poiché di fatto non è realmente incisivo (nel caso analizzato non indica nessun genere), vorremmo quindi eliminarlo.

3.3.3 Ridurre la dimensionalità con SVD

Supponiamo di voler rappresentare una matrice molto grande attraverso le sue componenti $U$, $V$ e $\Sigma$ ottenute attraverso la SVD. Tuttavia, anche queste ultime risultano essere molto grandi da conservare. Il miglior modo per ridurre la dimensionalità delle tre matrici è azzerare il valore singolare di $\Sigma$ più piccolo e, di conseguenza, eliminare le corrispondenti colonne nelle matrici $U$ e $V$.

Riprendiamo l'esempio precedente: supponiamo di voler passare da 3 dimensioni a 2. Il valore singolare più piccolo risulta essere 1.3, per cui lo azzeriamo e rimuovamo la terza colonna di $U$ e la terza riga di $V^T$: $$\hat{M}=(U)\left[\begin{array}{cc}.13& .02\\ .41& .07\\ .55& .09\\ .68& .11\\ .15& -.59\\ .07& -.73\\ .07& -.29\end{array}\right](\Sigma )\left[\begin{array}{cc}12.4& 0\\ 0& 9.5\end{array}\right](V^T)\left[\begin{array}{ccccc}.58& .59& .56& .09& .09\\ .12& -.02& .12& .69& .69\end{array}\right]$$ La matrice $\hat{M}$ risultante dal prodotto $U\Sigma V^T$ non coincide perfettamente con $M$, ma ne è una buona approssimazione. Se calcoliamo l'RMSE (root mean square error) attraverso la norma di Frobenius sulla matrice $M-\hat{M}$ otteniamo: $$\text{RMSE}=||M-\hat{M}|{|}_F=\sqrt{\sum _{ij}(M_{ij}-{\hat{M}}_{ij}{)}^2}$$ Calcolando l'errore di approssimazione attraverso la metrica RMSE, è possibile dimostrare che $\hat{M}$ ottenuta rimuovendo i valori singolari più piccoli, è la "best low rank approximation" di $M$, ovvero l'approssimazione migliore ottenibile dalle 3 matrici $U$, $V$ e $\Sigma$.

3.3.4 Best low rank approximation theorem

Sia $A=U\Sigma V^T$ e $B=US{V}^T$ dove $S$ è una matrice diagonale di dimensioni $r\times r$ con: $$s_{ii}=\{\begin{array}{l}{\sigma }_{i}i\text{ if }i=1,\dots ,k\\ 0\text{ altrimenti }\end{array}$$ allora $B$ è la migliore apporssimazione di rango $\rho =k$ di $A$, ovvero: $$B=\text{arg}\underset{B}{\min }||A-B|{|}_F\text{ dove }\rho (B)=k$$

3.3.5 Legami con la decomposizione spettrale

La SVD è legata alla autodecomposizone o decomposizione spettrale di una matrice. Per il teorema spettrale abbiamo che: $$A{A}^T=X\Lambda X^T$$ Dove $\Lambda$ (diagonale) ed $X$ contengono rispettivamente gli autovalori ed autovettori della matrice $A{A}^T$. Calcolando la SVD di $A$ abbiamo: $$A{A}^T=\left(U\Sigma V^T\right)(V{\Sigma }^T{U}^T)$$ Essendo $\Sigma$ una matrice diagonale, abbiamo che $\Sigma ={\Sigma }^T$, continuiamo: $$A{A}^T=U\Sigma V^{T}V\Sigma U^T=U\Sigma \Sigma U^T=U{\Sigma }^2{U}^T$$ In analogia alla decomposizione spettrale, possiamo dire che la matrice ${\Sigma }^2$ contiene gli autovalori della matrice $A{A}^T$, mentre la matrice $U$ ne contiene gli autovettori. Ripetendo lo stesso procedimento con $A^{T}A$ otterremo: $$A^{T}A=V{\Sigma }^2{V}^T$$ Per cui vi è un legame tra le due decomposizioni.

3.3.6 Azzerare i valori singolari piccoli funziona

Dato che $A=U\Sigma V^T$, allora $$A={\sigma }_1{u}_1{v}_1^T+\cdots +{\sigma }_k{u}_k{v}_k^T$$

Dato che $u_i$ è di dimensione $n\times 1$ e $v_i^T$ è di dimensione $1\times m$, allora il prodotto è una matrice.

Settare ${\sigma }_i=0$ (dove ${\sigma }_i$ è il valore singolare più piccolo) funziona perché essendo $u_i$ e $v_i$ vettori unitari, il prodotto con il valore ${\sigma }_i$ scala i valori della matrice. Quindi eliminare il ${\sigma }_i$ più piccolo introduce meno errore di approssimazione.

3.3.7 Quanti valori singolari mantenere

Una regola empirica per scegliere il numero $k$ di valori singolari da mantenere consiste nel mantenere almeno l'$80$% (o il $90$%) dell'energia. Ovvero, supponendo che il rango della matrice $A$ sia $\rho (A)=r$ e di voler ridurre la dimensione della decomposizione, allora si sceglie $k$ tale che: $$\sum _{i=1}^k{\sigma }_i\ge \left(\sum _{i=1}^r{\sigma }_i\right)\cdot 0.8$$

3.3.8 Complessità della decomposizione

I migliori algoritmi di calcolo della decomposizione SVD hanno una complessità temporale $O(n{m}^2)$ o $O(m{n}^2)$, a seconda di quale è minore. Tuttavia vi è meno lavoro necessario se si vogliono ottenere solo i valori singolari (o i primi $k$ valori singolari), o se la matrice è sparsa.

3.3.9 Query utilizzando i concetti

Consideriamo la matrice dell'esempio precedente: $$(M)\left[\begin{array}{ccccc}1& 1& 1& 0& 0\\ 3& 3& 3& 0& 0\\ 4& 4& 4& 0& 0\\ 5& 5& 5& 0& 0\\ 0& 0& 0& 4& 4\\ 0& 0& 0& 5& 5\\ 0& 0& 0& 2& 2\end{array}\right]=(U)\left[\begin{array}{cc}.14& 0\\ .42& 0\\ .56& 0\\ .70& 0\\ 0& .60\\ 0& .75\\ 0& .30\end{array}\right](\Sigma )\left[\begin{array}{cc}12.4& 0\\ 0& 9.5\end{array}\right](V^T)\left[\begin{array}{ccccc}.58& .58& .58& 0& 0\\ 0& 0& 0& .71& .71\end{array}\right]$$ Supponiamo che un nuovo utente abbia valutato un solo film, il primo, e che lo abbia valutato positivamente. Indichiamo il nuovo utente con il vettore riga $q=[4,0,0,0,0]$. È possibile mappare le valutazioni del nuovo utente nello "spazio dei concetti" moltiplicandolo per la matrice $V$ della decomposizione: $$qV=[4,0,0,0,0]\cdot \left[\begin{array}{cc}.58& 0\\ .58& 0\\ .58& 0\\ 0& .71\\ 0& .71\end{array}\right]=[2.32,0]$$ Dato che la prima componente del vettore risultante vale 2.32, mentre la seconda vale 0, possiamo derivarne che il nuovo utente è interessato a film di fantascienza (la prima categoria), mentre non è interessato a film d'amore. Il vettore risultante è una rappresentazione del vettore delle valutazioni nello spazio dei concetti. Possiamo mappare il vettore $qV$ nuovamente nello spazio dei film moltiplicandolo per $V^T$ $$qV{V}^T=[2.32,0]\cdot \left[\begin{array}{ccccc}.58& .58& .58& 0& 0\\ 0& 0& 0& .71& .71\end{array}\right]=[1.35,1.35,1.35,0,0]$$ Questo ci suggerisce che il nuovo utente potrebbe essere interessato al secondo ed al terzo film. Un altro tipo di query consiste nel trovare utenti con interessi simili, mappando le loro valutazioni nello spazio dei concetti e calcolando la similarità tra i due vettori attraverso la distanza del coseno, che ci fornisce la differenza delle direzioni dei vettori.

Supponiamo che due vettori delle valutazioni mappati nello spazio dei concetti assumano valori $[2.32,0]$ e $[1.74,0]$ rispettivamente. I due vettori hanno la stessa direzione: entrambi si trovano sull'asse del concetto "fantascienza", per cui hanno gusti analoghi e la distanza del coseno è 0.

3.3.10 Conclusioni

La SVD è una buona decomposizione grazie al teorema sulla approssimazione low-rank ottimale. Tuttavia è di difficile interpretazione, poiché i vettori singolari specificano combinazioni lineari di colonne e righe di input, e le matrici ottenute non sono sparse, quindi mantenerle in memoria potrebbe essere problematico.

3.4 CUR decomposition

Spesso la matrice da decomporre è molto sparsa. Utilizzando la decomposizione SVD, le matrici $U$, $\Sigma$ e $V$ sono dense. Idealmente si vuole che la decomposizione di una matrice sparsa sia altrettanto sparsa. La decomposizione CUR cerca di garantire questa proprietà. Questo metodo seleziona un insieme di colonne $C$ e un insieme di righe $R$ che giocano il ruolo di $U$ e $V^T$ nella SVD. La scelta delle righe e delle colonne è fatta in maniera casuale con una distribuzione che dipende dalla norma di Frobenius. Tra le matrici $C$ ed $R$ vi è una matrice quadrata $U$ costruita come pseudo-inversa dell'intersezione delle righe e delle colonne scelte.

3.4.1 Definizione di CUR

Sia $M$ una matrice di dimensione $m\times n$. Si scelgano $r$ concetti da utilizzare nella decomposizione. Una decomposizione $CUR$ di $M$ è formata da:

• Una matrice $C$ di dimensione $m\times r$ formata da $r$ colonne prese casualmente da $M$;
• Una matrice $R$ di dimensione $r\times n$ formata da $r$ righe prese casualmente da $M$;
• Una matrice $U$ di dimensione $r\times r$ costruita da $C$ ed $R$.

La matrice $U$ viene costruita mediante il seguente processo:

• Sia $W$ una matrice $r\times r$ data dall'intersezione di $C$ ed $R$, ovvero l'elemento $W_{ij}$ corrisponde all'elemento di $M$ la cui colonna è la $j$-esima colonna di $C$ e la cui riga è la $i$-esima riga di $R$;
• Si effettua la decomposizione SVD su $W$, quindi $W=X\Sigma Y^T$;
• Si calcola la matrice pseudoinversa ${\Sigma }^{+}$ di Moore-Penrose della matrice diagonale $\Sigma$, dove ogni elemento della diagonale non nullo ${\sigma }_{ii}\ne 0$ si rimpiazza con l'elemento $\frac{1}{{\sigma }_{ii}}$. Se l'elemento della diagonale è nullo, allora si lascia nullo.
• Si ottiene $U=Y({\Sigma }^{+}{)}^2{X}^T$.

Perché la pseudoinversa funziona?

Scomponiamo la matrice $M$ utilizzano la SVD $M=XZY$, allora deve accadere che $M^{-1}=Y^{-1}{Z}^{-1}{X}^{-1}$. Essendo $X$ ed $Y$ ortonormali, la loro trasposta corrisponderà all'inversa. Quindi scriviamo $M^{-1}=Y^T{Z}^{-1}{X}^T$. Poiché la matrice $Z$ è diagonale, allora $Z^{-1}=\frac{1}{Z}$, dove gli elementi in $Z$ nulli vengono però mantenuti nulli (altrimenti si avrebbe una divisione per zero). Se $M$ è non singolare (determinante diverso da zero, di conseguenza esiste l'inversa $M^{-1}$) allora la pseudo-inversa coincide con la vera inversa.

3.4.2 Teorema [Drineas et al.]

Sia $CUR$ la decomposizione di $A$ calcolata in tempo $O(mn)$, allora si dimostra che: $$||A-CUR|{|}_F\le ||A-A_k|{|}_F+ϵ||A|{|}_F$$ Con probabilità $1-\delta$, selezionando: $$O\left(k\frac{log(\frac{1}{\delta })}{{ϵ}^2}\right)\text{ colonne e }O\left(k^2\frac{lo{g}^3(\frac{1}{\delta })}{{ϵ}^6}\right)\text{ righe}$$

Nella pratica basta selezionare $4\times k$ righe e colonne, dove $k$ è il valore della "best k-rank approximation" nell'espressione 54, calcolata attraverso la decomposizione SVD azzerando gli $(r-k)$ valori singolari più piccoli.

Fissati $ϵ$ e $\delta$ arbitrariamente, tale teorema ci fornisce il numero di righe e colonne da selezionare per dare un limite superiore all'errore di approssimazione con una certa probabilità.

3.4.3 Selezionare righe e colonne

Anche se la scelta delle righe e delle colonne è casuale, tale scelta deve essere direzionata in qualche modo tale da selezionare le righe e le colonne più importanti. La misura di importanza è data dal quadrato della norma di Frobenius: $$f=\sum _{ij}{m}_{ij}^2$$ La probabilità $p_i$ di scegliere la $i$-esima riga di $M$ è calcolata come segue: $$p_i=\sum _j\frac{m_{ij}^2}{f}$$ La probabilità $q_i$ di scegliere la $i$-esima colonna di $M$ è calcolata come segue: $$q_i=\sum _j\frac{m_{ji}^2}{f}$$ Data la distribuzione di probabilità di righe e colonne, essendo che ogni selezione è indipendente dalle altre, notiamo che le righe con più alta probabilità possono essere selezionate più volte; torneremo più avanti su questo aspetto.

Una volta selezionata con probabilità assegnata una colonna $i$ dalla matrice $M$, gli elementi di tale colonna vengono scalati (quindi divisi) di un fattore $\sqrt{r{q}_i}$, la colonna scalata diventa poi una colonna della matrice $C$. Allo stesso modo, selezionata una riga $i$ con probabilità assegnata dalla matrice $M$, gli elementi di tale riga vengono scalati di un fatore $\sqrt{r{p}_i}$, quindi la riga scalata diventa una riga della matrice $R$.

3.4.4 Teorema sull'upper bound dell'approssimazione

Ipotizziamo di selezionare un numero analogo di righe e colonne $c=r=O(\frac{k\log k}{{ϵ}^2})$ attraverso le distribuzioni di probabilità assegnate dall'algoritmo CUR. Costruiamo quindi le matrici $C$, $U$ ed $R$, allora: $$P(||A-CUR|{|}_F\le (2+ϵ)||A-A_k|{|}_F)\approx 0.98$$

3.4.5 Righe e colonne duplicate

La decomposizione CUR è vantaggiosa perché facile da interpretare (i vettori della base sono righe e colonne della matrice) ed inoltre ha una base sparsa. Tuttavia, è possibile riscontrare duplicazioni su colonne e righe a causa della distribuzione di probabilità basata sulle norme: colonne e righe con norme alte verranno selezionate spesso.

Supponiamo che la matrice $C$ abbia $k$ colonne duplicate, possiamo ridurre queste $k$ colonne ad una sola colonna, diminuendo così il numero totale di colonne di $C$. Allo stesso modo, se $R$ ha $k$ righe duplicate, allora è possibile ridurle ad una sola riga, diminuendo il numero di righe totale di $R$. Tuttavia, tale riga o colonna rimanente dovrà essere scalata moltiplicando ad ogni elemento il valore $\sqrt{k}$.

Supponiamo che la matrice $C$ di dimensione $m\times r$ diventi di dimensione $m\times r^{\prime }$ dopo la rimozione dei duplicati. Supponiamo che la matrice $R$ di dimensione $r\times n$ diventi di dimensione $r^{\prime \prime }\times n$ dopo la rimozione dei duplicati. Se il numero di duplicati è diverso in $C$ ed $R$ ($r^{\prime }\ne r^{\prime \prime }$) allora la matrice di intersezione non sarà quadrata. Possiamo comunque calcolare la pseudoinversa dalla decomposizione di $W=X\Sigma Y^T$, dove $\Sigma$ è una matrice diagonale con alcune colonne o righe nulle (dipeso dalla dimensione maggiore). Si calcola la pseudoinversa canonicamente, e si esegue la trasposizione del risultato. Supponiamo: $$\Sigma =\left[\begin{array}{cccc}2& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 3& 0\end{array}\right]$$ Allora: $${\Sigma }^{+}=\left[\begin{array}{ccc}\frac{1}{2}& 0& 0\\ 0& 0& 0\\ 0& 0& \frac{1}{3}\\ 0& 0& 0\end{array}\right]$$

3.4.6 Ottimizzazione dell'algoritmo

Si dimostra che per migliorare l'accuratezza della decomposizione (sulla base della norma di Frobenius), è sufficiente selezionare righe (o colonne) che siano ortogonali (quindi linearmente indipendenti) tra di loro.

3.5 NNMF - Non-negative matrix factorization

Sia $A$ una matrice di dimensione $f\times n$, in cui le $n$ colonne della matrice rappresentano le osservazioni di un insieme di dati, mentre le $f$ righe della matrice sono le corrispondenti feature. La tecnica NNMF ci permette di ottenere una decomposizione: $$A\approx WH$$ Vogliamo ridurre il numero di feature da $f$ a $k$. Le matrici avranno dimensione $W\in {\mathbb{R}}^{f\times k}$ e $H\in {\mathbb{R}}^{k\times n}$. L'interpretazione di $W$, chiamata anche matrice dizionario, consiste nel considerare ogni colonna come un vettore base, quindi un vettore che affiora frequentemente nelle osservazioni.

L'interpretazione di $H$, chiamata anche matrice di attivazione o di espasione, consiste nel considerare ogni colonna come coordinate di una osservazione rispetto alla base $W$. Quindi ci permette di ricostruire una approssimazione dell'osservazione originale attraverso una combinazione lineare delle basi in $W$.

$W$ ed $H$ sono due matrici con elementi non negativi, ovvero $w_{fk},h_{k,n}\ge 0$. Il rango $k$ della fattorizzazione è scelto in modo tale che $(f+n)k<fn$ ed il prodotto $WH$ è una rappresentazione compressa di $A$. La non-negatività delle matrici $W$ ed $H$ induce sparsità.

3.5.1 Definizione di NNMF

Sia $A\in {\mathbb{R}}^{f\times n}$. Con $a_i$ indicheremo l'$i$-esima colonna di $A$ $$a_i=\left[\begin{array}{c}{a}_{1i}\\ a_{2i}\\ \dots \\ a_{fi}\end{array}\right]a_i\in {\mathbb{R}}_{+}^f$$ Sia $W\in R^{f\times k}$. Con $w_i$ indicheremo l'$i$-esima colonna di $W$ $$w_i=\left[\begin{array}{c}{w}_{1i}\\ w_{2i}\\ \dots \\ w_{fi}\end{array}\right]w_i\in {\mathbb{R}}_{+}^f$$ In generale $k<r$. Il vettore colonna $w_i$ è un vettore base.

Sia $H\in R^{k\times n}$. Con $h_j$ indicheremo la $j$-esima colonna di $H$ $$h_j=\left[\begin{array}{c}{h}_{1j}\\ h_{2j}\\ \dots \\ h_{kj}\end{array}\right]h_j\in {\mathbb{R}}_{+}^k$$ Il vettore colonna $h_j$ corrisponde all'osservazione $a_j$ rappresentata secondo la base formata dai $k$ vettori colonna della matrice $W$.

Approssimeremo la feature $i$-esima della $j$-esima osservazione della matrice $A$ attraverso il prodotto scalare tra la riga $i$-esima della matrice $W$, che corrisponde all'$i$-esima componente di ogni vettore base, per la $j$-esima colonna della matrice $H$, ovvero la $j$-esima rappresentata attraverso la base $W$. $$a_{ij}\approx \left[\begin{array}{cccc}{w}_{i1}& w_{i2}& \dots & w_{ik}\end{array}\right]\left[\begin{array}{c}{h}_{1j}\\ h_{2j}\\ \dots \\ h_{k_j}\end{array}\right]=\sum _{k=1}^k\left(w_{ik}\cdot h_{kj}\right)$$

3.5.2 Legame con Probabilistic Latent Semantic Analysis

Supponiamo che la matrice $A$ sia una matrice di co-occorrenza: sulle colonne sono disposti i documenti $d$, sulle righe i termini $m$. L'elemento $a_{ij}$ indica quante volte il termine $m_i$ appare nel documento $d_j$. Supponendo di introdurre il concetto di topic $t$, quindi tematica trattata da un insieme di documenti, il modello PLSA asserisce che: $$P(m_i,d_j)=\sum _{k=1}^{K}P(t_k)P(d_j\mid t_k)P(m_i\mid t_k)$$ Ovvero la probabilità di trovare il termine $m_i$ all'interno del documento $d_j$. Tornando alla decomposizione NNMF, possiamo costruire un modello legato alla PLSA, assumendo che: $$w_{fk}=P(t_k)P(m_f\mid t_k)$$ e anche che $$h_{kn}=P(d_n\mid t_k)$$ quindi possiamo riscrivere il modello come $$[\hat{P}(m_f,d_n)]=[{\hat{a}}_{fn}]=WH$$ Dove le basi $w_k$ in $W$ rappresentano concetti in grado di spiegare i dati analizzati utilizzando i relativi coefficienti in $h_k$.

3.5.3 Funzione obiettivo

Le matrici $W$ e $H$ si ottengono minimizzando una certa funzione obiettivo, quindi: $$W,H=\text{arg}\underset{W,H\ge 0}{\min }D(A\mid WH)$$ Due possibili funzioni obiettivo sono la distanza Euclidea $$\sum _{f,n}{\left(a_{fn}-{\hat{a}}_{fn}\right)}^2$$ O la divergenza di Kullback-Leibler (KL) $$\sum _{fn}\left(a_{fn}\log \frac{a_{fn}}{{\hat{a}}_{fn}}-a_{fn}+{\hat{a}}_{fn}\right)$$ Dove con ${\hat{a}}_{fn}$ indichiamo il valore stimato di $a_{fn}$ dal prodotto $WH$.

3.5.4 Calcolo della NNMF

La NNMF di una matrice $A$ può essere calcolata iterando un processo sino a convergenza. Supponiamo di inizializzare le matrici $W$ ed $H$ in maniera casuale. Ricalcoliamo ad ogni iterazione le due matrici come segue: $$w_{ia}=w_{ia}\sum _{\mu }\frac{a_{i\mu }}{{\hat{a}}_{i\mu }}{h}_{a\mu }$$ Dopodiché normalizziamo il risultato: $$w_{ia}=\frac{w_{ia}}{{\sum }_j{h}_{aj}}$$ Allo stesso modo calcoliamo la matrice $H$ $$h_{a\mu }=h_{a\mu }\sum _i{w}_{ia}\frac{a_{i\mu }}{{\hat{a}}_{i\mu }}$$ Dopodiché normalizziamo il risultato: $$h_{a\mu }=\frac{h_{a\mu }}{{\sum }_j{w}_{ja}}$$ Le iterazioni convergono ad un massimo locale della seguente funzione obiettivo, che risulta essere una derivazione della divergenza di KL (in cui si rimuovono i termini costanti): $$X=\sum _i^f\sum _{\mu }^n\left[a_{i\mu }\log ({\hat{a}}_{iu})-{\hat{a}}_{iu}\right]$$

Assunzione di linearità Nelle decomposizioni affrontate si proiettano linearmente i punti da uno spazio ad un altro, preservando la distanza Euclidea. Altri metodi permettono di effettuare delle proiezioni non lineari (i.e. isomap), in cui i punti ricadono in una curva (manifold) a più bassa dimensione.