Dive into data mining
Dal materiale didattico dei seguenti corsi:
- Social Media Management - Prof. Antonino Furnari - aa 2020/21
- Introduzione al Data Mining - Prof. Alfredo Ferro, Prof. Giovanni Micale - aa 2020/21
- Big Data - Prof. Alfredo Pulvirenti -- aa 2020/21
Dipartimento di matematica e informatica - UniCT
Appunti a cura di Lemuel Puglisi.
Referenze:
- Bishop, Christopher M. Pattern recognition and machine learning;
- Z. Aston Zhang, Zachary Lipton, Mu Li, Alexander Smola, Dive into Deep Learning;
Data mining
1. Introduzione
Il data mining consiste nell'estrazione di regolarità da grandi quantità di dati attraverso analisi, talvolta complesse, ed algoritmi efficienti e scalabili. Le informazioni cercate possono essere di vario genere:
- Dipendenze tra dati
- Individuazione di classi (cluster)
- Descrizione delle classi (cluster)
- Individuazione di outliers / eccezioni
Le aree applicative di tali studi sono generalmente l'analisi ed il supporto alle decisioni. Tuttavia, il target include anche text mining, analisi del web, intelligent query answering etc.
2. Market Basket Analysis
Per introdurre il concetto di regole associative, presentiamo una applicazione paradigmatica di esse: il Market Basket Analysis (MBA). Supponiamo di avere un insieme di oggetti (items) ed un insieme di carrelli (baskets) che correlano gli oggetti tra loro. L' MBA trova la correlazione tra gli oggetti studiando la relazione molti-a-molti con i carrelli. Tale tecnologia si concentra su eventi comuni anziché rari (outliers).
Ipotizziamo di voler trovare l'insieme di oggetti che appare frequentemente all'interno dei carrelli. Sia I l'insieme di oggetti (Itemset), definiamo il supporto (Support) per I come il numero di carrelli contenenti tutti gli oggetti di I. A volte il supporto è espresso in percentuale (relativamente al numero di carrelli totali). Sia s la soglia o support threshold, definiamo insiemi frequenti gli insiemi che appaino in almeno s carrelli.
2.1 Applicazione 1 - Supermercato
Ipotizziamo che i prodotti di un supermercato siano gli oggetti e gli scontrini siano i carrelli, poiché mettono in relazione gli oggetti tra di loro. Una delle possibili applicazioni consiste nel trovare quali sono i prodotti acquistati insieme più frequentemente dai clienti. Una ricerca effettuata in America ha prodotto come risultato la correlazione tra pannolini e birra. Una volta estratta la correlazione, è possibile scontare il prezzo dei pannolini ed aumentare quello della birra (facendo attenzione al verso di acquisto, che in questo caso è pannolini > birra).
2.2 Applicazione 2 - Plagiarism detection
Ipotizziamo che dei documenti testuali siano gli oggetti e che delle frasi siano i carrelli. Più documenti possono contenere la stessa frase, per cui connettono gli oggetti tra loro. È possibile notare come i carrelli non debbano necessariamente contenere gli oggetti, bensì correlarli in qualche modo tra loro. L'obiettivo della computazione potrebbe essere quello di scoprire dei plagi attravero documenti che compaiono spesso insieme, ovvero che formino un insieme frequente.
2.3 Applicazione 3 - Web analysis
Ipotizziamo che delle parole siano gli oggetti e che le pagine web siano i carrelli, poichè esse contengono le parole e le mettono in relazione. Parole che appaiono frequentemente insieme nelle pagine web potrebbero indicare una interessante relazione. Affronteremo nel cap. 13 alcuni cenni di analisi testuale.
3. Regole associative
Le regole associative sono regole del tipo se-allora (if-then) sul contenuto dei basket e sono della forma: ovvero: "Se il basket contiene gli oggetti allora molto probabilmente conterrà anche ". Definiamo la confidenza (confidence) di una regola di associazione come la probabilità di dati .

3.1 Trovare le regole di associazione
Supponiamo di voler trovare tutte le regole di associazione tali che abbiano un supporto maggiore di s ed una confidenza maggiore di c. Si noti che per supporto si intende il supporto dell'itemset alla sinistra della regola. La parte computazionalmente difficile ed onerosa sta nel trovare gli insiemi frequenti.
Osservazione:
3.2 Problemi pratici
Tipicamente i file contenenti i dati sono memorizzati nel disco (es. flat files, database). Data la massiva cardinalità dei dati, il costo principale degli algoritmi è dato dal numero di letture da disco.
4. Algoritmi di ricerca di coppie frequenti
Analizzando un algoritmo di ricerca degli insiemi frequenti, scoviamo subito che il costo principale è quello di cercare tra tutte le coppie: con 10k elementi, le coppie sono circa 10k*2 elementi. In generale, dato l'insieme formato da elementi, l'insieme delle parti (power set) ha cardinalità , ovvero si avranno itemset da analizzare, per cui la ricerca esaustiva prenderebbe tempo esponenziale . Vedremo che sarà meno oneroso il compito di cercare triple, quadruple etc.
In generale: la probabilità di essere insiemi frequenti diminuisce esponenzialmente all'aumentare della dimensione della tupla. Il perché è dimostrabile in termini probabilistici. Vediamo adesso alcuni algoritmi che si occupano della ricerca di coppie frequenti.
4.1 Naive algorithm
L'algoritmo naive legge una sola volta l'intero file e, per ogni basket contenente elementi, genera coppie da analizzare. Il numero di coppie è dato dalle combinazioni degli item in 2 posizioni, calcolabile attraverso il coefficiente binomiale: Definiamo una struttura apposita (es. una matrice) che contenga tutti gli item sia nelle righe che nelle colonne. Per ogni coppia di item all'interno del basket incrementa l'occorrenza della coppia nella struttura. Tale algoritmo fallisce se provoca un overflow in memoria primaria (gli item potrebbero essere dell'ordine dei miliardi). Supponiamo vi siano 105 elementi in memoria e quindi: Saranno necessari circa 20 GB di memoria primaria. Vi sono 2 approcci tipici al conteggio delle occorrenze delle coppie: la matrice triangolare e la tabella di triple.
4.1.1 Matrice triangolare
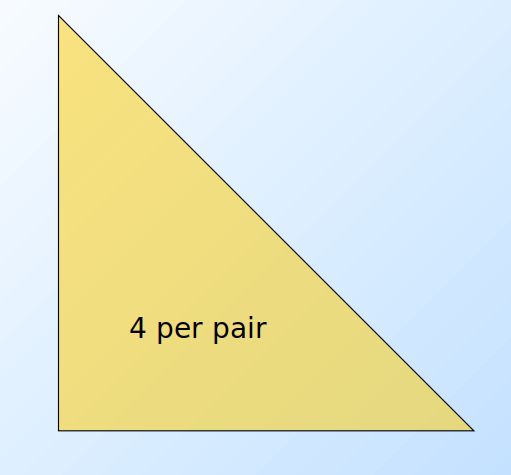
Tale approccio consiste nel contare tutte le coppie attraverso una matrice triangolare. Supponendo che la matrice sia composta da interi, essa richiede 4 byte per paio. Supponiamo che le coppie vengano così considerate: Dati gli indici i,j è possibile effettuare una linearizzazione delle posizioni, sfruttando un array monodimensionale di dimensione n(n-1)/2 anziché una matrice. Nello specifico:
4.1.2 Tabella di triple
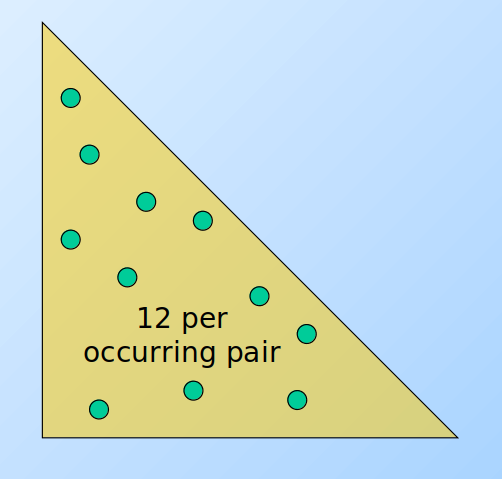
Un altro approccio consiste nel contare solo le coppie effettivamente presenti nei basket, quindi tenere una tripla di valori (i, j, c) tale che la coppia {i,j} abbia c occorrenze, con c > 0. Ogni tripla richiede 12 bytes, ma non tutte le coppie sono presenti in memoria. Tale approccio risulta conveniente rispetto alla matrice solo se occorrono al più 1/3 delle coppie totali, a causa del triplo della memoria utilizzata per ogni coppia (12 byte rispetto ai 4 della matrice). Potrebbe servire ulteriore spazio per strutture che facilitano l'accesso alla tabella, come delle hash table.
4.2 A-Priori Algorithm
L'algoritmo a-priori è diviso in due passaggi principali e limita la necessità di memoria primaria. L'idea principale è quella della monotonicità (monotonicity): se un insieme S di item appare almeno k volte, allora anche tutti i sottoinsiemi di S appaiono almeno k volte.
Contropositivo per le coppie: Se un item i non appare in almeno s basket, allora nessuna coppia contenente i potrà apparire in almeno s basket.
Passo 1: Leggere tutti i basket e contare in memoria principale le occorrenze di ogni item. Questo passaggio richiede che la memoria sia almeno proporzionale al numero di item. Consideriamo item frequenti (frequent items) gli item che compaiono almeno s volte.
Passo 2: Leggere nuovamente i basket, ma contare in memoria principale solo le coppie formate dagli elementi frequenti trovati al passo 1. Tale passo richiede una memoria proporzionale al quadrato del numero di elementi frequenti, più una lista degli elementi frequenti.
È possibile utilizzare una matrice triangolare che referenzia solo gli item frequenti (o utilizzare il metodo delle triple). La mappatura degli item frequenti nella matrice sarà diversa da quella originale, per questo è consigliato tenere una tabella che ricolleghi gli indici della matrice con quelli originali.
Supponiamo di voler trovare tuple di item di ordine k maggiore al secondo. Per ogni k consideriamo due insiemi:
- Ck = itemset di cardinalità k candidati ad essere frequenti, ovvero con un supporto > s, basandosi sulle informazioni degli itemset di cardinalità k-1.
- Lk = itemset di cardinalità k effettivamente frequenti.
A partire dall'insieme C1 di tutti gli item viene svolto il primo passo dell'algoritmo e prodotto l'insieme L1 degli item frequenti. Da quest'ultimo, viene costruito l'insieme delle coppie C2 ed un secondo filtraggio produce gli insiemi frequenti di cardinalità 2 L2. Lo stesso procedimento viene eseguito per k=3, 4, ... e si può dimostrare che all'aumentare di k, l'algoritmo tende ad andare a convergenza più velocemente (in maniera esponenziale).
Per dati tipici nel MBA e un supporto richiesto dell'1%, k=2 richiede la maggior parte della memoria.
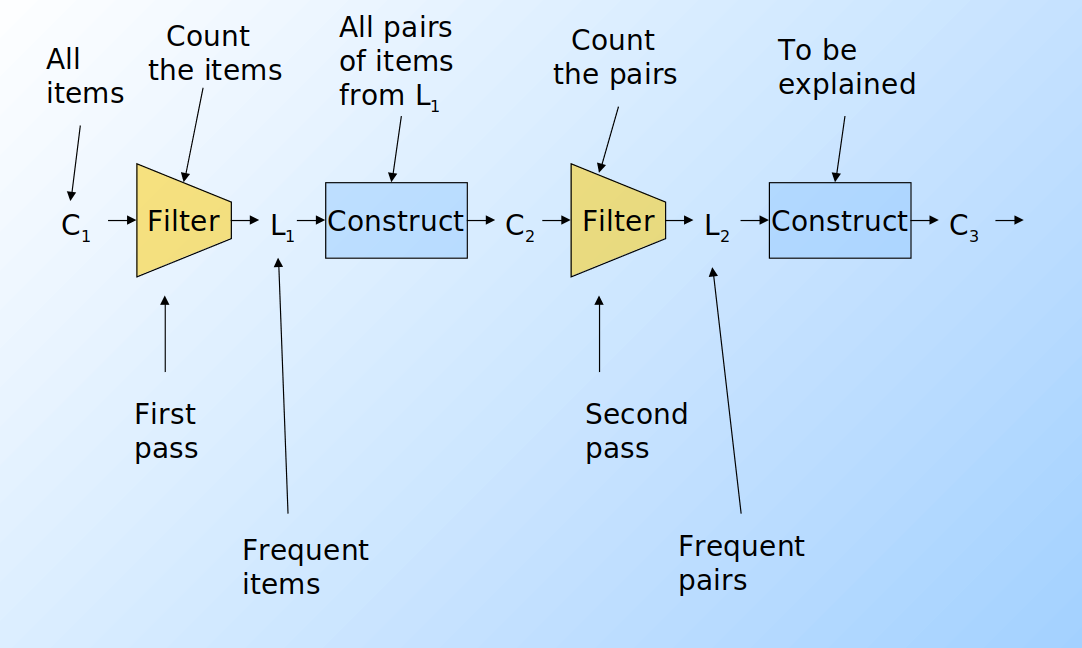
Osservazioni:
- C
1rappresenta tutti gli elementi - L
kè composto da membri di Ckil cui supporto è > s - C
k+1è composto da insiemi in cui esiste un sottoinsieme residente in Lk
Clustering
1. Introduzione
Il clustering è un processo che consiste nel raggruppare un insieme di oggetti in gruppi detti cluster, sulla base di una nozione di distanza tra gli oggetti. L'obiettivo del clustering è quello di raggruppare nello stesso cluster oggetti "simili" tra loro (o con bassa distanza reciproca) e in cluster diversi oggetti "dissimili" tra loro (o ad elevata distanza).
1.1 Unsupervised learning
Il clustering è un processo di unsupervised learning (apprendimento non supervisionato): si vuole suddividere un insieme di dati in n classi (o cluster) senza alcuna conoscenza a-priori di quante e quali siano le classi e le loro etichette.
Esistono invece dei task, come la classificazione o la predizione, che necessitano di un apprendimento supervisionato (supervised learning). Partendo da un training set essi allenano un modello in grado di classificare nuovi dati o predire valori.
2. Spazi metrici e funzione distanza
Gli oggetti da raggruppare rappresentano punti appartenenti ad uno spazio metrico, cioè uno spazio in cui è definita una funzione distanza D. La definizione di una funzione distanza è cruciale per effettuare il clustering. Una funzione D definita su una coppia di punti di uno spazio metrico S è una misura di distanza se soddisfa le seguenti proprietà:
2.1 Spazio euclideo
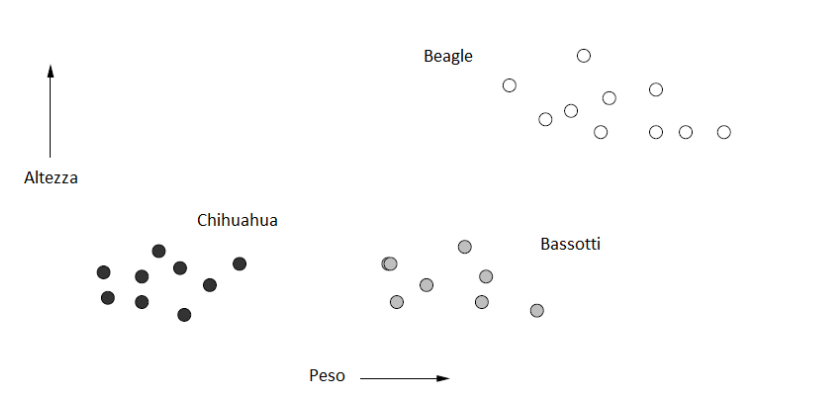
L'esempio più comune di spazio metrico è lo spazio euclideo ad n dimensioni , in cui i punti dello spazio sono vettori di numeri reali. La quantità n rappresenta il numero di dimensioni dello spazio. Le componenti dei vettori sono comunemente chiamate coordinate dei corrispondenti punti. Nelle applicazioni reali, le coordinate rappresentano gli attributi (o "features") degli oggetti dello spazio metrico. Una proprietà caratteristica degli spazi euclidei è che la media di un insieme di punti nello spazio è sempre definita ed è un punto nello spazio, chiamato centroide o centro geometrico. Di seguito è riportato un esempio di oggetti (cani) classificati in uno spazio euclideo a 2 dimensioni, secondo 2 attributi: altezza e peso.
2.1.1 Distanze nello spazio Euclideo
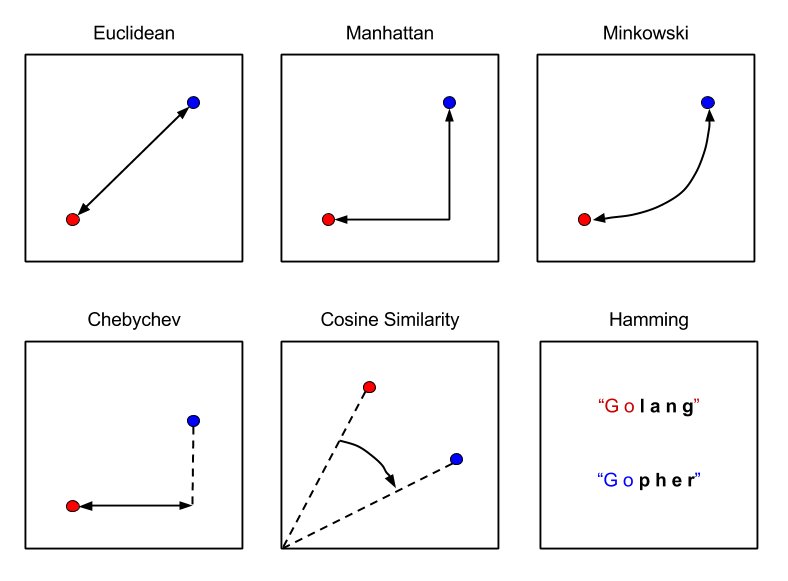
Nello spazio euclideo è possibile definire diverse misure di distanza valide (che rispettino le 3 proprietà). La funzione distanza più utilizzata è la distanza euclidea: Siano e due punti nello spazio , la distanza euclidea è così definita:
Esistono altri tipi di distanze, come la distanza di Manhattan La norma è una generalizzazione della distanza euclidea dove sia la radice che l'esponente assumono un valore r, anziché 2: La norma prende la distanza massima tra le componenti delle n dimensioni: La distanza del coseno misura la distanza dal punto di vista angolare:
2.2 Spazi non euclidei
In uno spazio non euclideo il concetto di centroide non è definito. Tuttavia, si può definire il concetto di 1-mediana come un punto che minimizza la distanza media (o equivalentemente la somma) delle distanza degli altri punti dell'insieme. Esempi di spazi non euclidei sono spazi in cui gli oggetti sono insiemi o stringhe.
Per alcuni spazi non euclidei (come le versioni discrete degli spazi euclidei, o spazi formati da vettori di interi) è possibile utilizzare le distanze euclidee già viste. Nel caso più generale occorre definire metriche alternative.
Es. con insiemi, distanza di Jaccard: Dati due insiemi T ed S, la distanza è definita come il complementare del rapporto tra la cardinalità dell'intersezione e la cardinalità dell'unione.
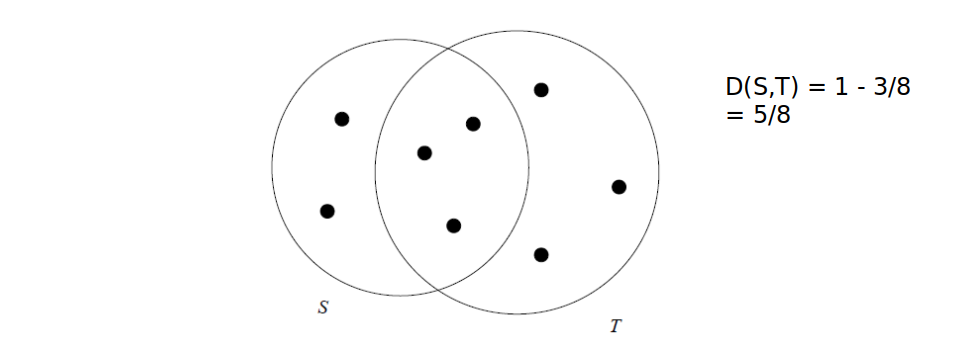
2.2.1 Dim. Distanza di Jaccard e proprietà triangolare
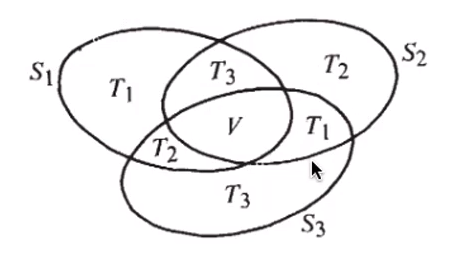
Dimostriamo che la distanza di Jaccard rispetta la proprietà triangolare: Dato che ha cardinalità minore di , possiamo maggiorare l'espressione come segue: Per cui la proprietà risulta dimostrata.
2.2.2 Distanza di Edit e distanza di Hamming
Distanza di edit: date due stringhe x e y, la distanza di edit è il minimo numero di operazioni di cancellazione e inserzione da effettuare partendo da x per ottenere y.
x = "abcde"
y = "acfdeg"
#1 cancella b => acde
#2 inserisci f dopo c => acfde
#3 inserisci g dopo e => acfdeg
D(x,y) = 3
Distanza di Hamming è il numero di componenti in corrispondenza delle quali x e y differiscono. Vediamo un esempio: Poiché differisce solo la terza componente.
3. Tassonomie degli algoritmi di clustering
Una classificazione degli algoritmi di clustering si basa sull'approccio utilizzato.
1) Metodi gerarchici o agglomerativi Ciascun punto viene inizialmente posto in un cluster diverso e successivamente i cluster vengono combinati tra loro secondo una nozione di vicinanza definita opportunamente. Il processo di aggregazione di cluster termina sulla base di un opportuno criterio di terminazione (es. raggiungimento di un numero di cluster desiderati).
2) Metodi di partizionamento L'insieme di punti viene partizionato in k cluster, in modo che ciascun punto appartenga ad uno e un solo cluster. Dopo aver stimato dei cluster iniziali, i punti vengono presi in considerazione seguendo un certo ordine e assegnati al cluster più adatto. Alcune varianti permettono di non assegnare un punto a nessun cluster se questo è un outlier (cioè è isolato e lontano dai vari cluster). Rappresentanti di questa categoria sono gli algoritmi k-means.
3) Metodi basati sulla densità I cluster prodotti inizialmente vengono estesi fino a quando la densità (ovvero il numero di punti) in un intorno più o meno grande supera una certa soglia. Tali metodi sono in grado di rilevare outlier e cluster di qualunque forma (non solo sferica come nel partizionamento). Esempi di questa classe sono DBSCAN e OPTICS.
4) Metodi basati sulla griglia Lo spazio viene quantizzato in un numero finito di celle che formano una struttura a griglia. Tutte le operazioni di clustering vengono quindi effettuate sullo spazio quantizzato, garantendo un tempo di elaborazione veloce, dipendente principalmente dal numero di celle di ogni dimensione dello spazio quantizzato. Un esempio è l'algoritmo STING.
5) Metodi basati sul modello Si ipotizza un modello per ogni cluster e si trova la migliore dispozione dei dati rispetto al determinato modello. Esempi di questa categoria sono gli algoritmi EM, COBWEB e SOM.
Altri criteri non meno importanti per distinguere gli algoritmi di clustering sono i tipi di spazio metrico e l'utilizzo della memoria secondaria.
4. Problema della dimensionalità
Spesso si ha a che fare con spazi ad elevata dimensione ed oggetti da clusterizzare con molti attributi. In spazi euclidei ad elevata dimensionalità si osservano delle proprietà interessanti e poco intuitive, riassunte con i termine <<curse of dimensionality>> (o problema della dimensionalità). Queste proprietà rendono molto più complicato il clustering.
Es. Se in un insieme di oggetti avessimo tanti attributi booleani rispetto ad un grande insieme di colori, e pochi attributi realmente rilevanti, la distanza di Hamming tra due oggetti tenderebbe alla dimensione di questi. Ogni oggetto sarebbe pressappoco equidistante dagli altri e formerebbe un cluster assestante. È importante quindi selezionare poche features discriminanti.
Al crescere del numero di features, il numero di dati necessari a rendere il clustering effettivamente utile aumenta in maniera esponenziale.
In generale, quasi tutte le coppie di punti in un insieme finito, definito in uno spazio con moltissime dimensioni, saranno equidistanti tra loro.
4.1 Distribuzione delle distanze in spazi ad alta dimensionalità
Consideriamo valori -dimensionali; supponiamo che le componenti varino casualmente nel range . Supponiamo che sia molto grande e misuriamo la distanza tra i punti attraverso la distanza euclidea. Siano e due punti, la distanza è calcolata come segue Essendo molto grande, con alta probabilità vi saranno due componenti la cui differenza sarà molto vicina ad 1, quindi il limite inferiore della distanza sarà circa 1. Nel caso limite in cui tutte le componenti differiscano di 1, allora il limite superiore della distanza sarà . La maggior parte dei punti avrà una distanza vicina alla media tra i due limiti. Se non vi punti vicini risulta complesso il raggruppamento in cluster.
4.2 Fattori chiave per gli algoritmi di clustering
In generale, non esiste un algoritmo di clustering migliore degli altri. La bontà di un algoritmo è legata a diversi fattori, non tutti necessariamente indispensabili per l'applicazione in esame:
- Scalabilità
- Capacità di trattare diversi tipi di attributi
- Capacità di cercare cluster di forma diversa
- Facilità nell'uso e nella comprensione dei parametri in input
- Capacità di gestire dati con outlier e rumore
- Insensibilità all'ordine dei record o all'esaminazione
- Capacità di gestire dati ad alta dimensionalità
- Interpretabilità e usabilità dei risultati ottenuti
5. Algoritmo di clustering gerarchico
Il clustering gerarchico è un metodo di analisi dei cluster che costruisce una gerarchia di cluster. Le caratteristiche salienti del clustering gerarchico sono riassumibili nei seguenti punti:
- Assegnare a ciascun punto un cluster separato.
- Unire i cluster più vicini in un unico cluster.
- Ripetere il secondo passo sino a quando non si è soddisfatto un criterio di terminazione.
Le domande chiave da porsi sono:
- Come rappresentare ciascun cluster?
- Come scegliere quali cluster unire e come definire la vicinanza tra cluster?
- Quale criterio di terminazione scegliere?
5.1 Rappresentazione dei cluster
Iniziamo considerando il caso degli spazi Euclidei: il cluster potrebbe essere rappresentato dal centroide (media o baricentro di tutti i punti del cluster). Il centroide è un punto nello spazio ma, in generale, non corrisponde ad un punto del cluster. Se viene scelto il centroide come rappresentante del cluster, un buon criterio per misurare la distanza tra i cluster consiste nel misurare la distanza dai relativi centroidi. L'algoritmo sceglierà ad ogni passo i due cluster la cui distanza tra i rispettivi centroidi è minima. Ogni qual volta vengono fusi due cluster, viene ricalcolato il centroide del cluster risultante.
5.1.1 Dendogramma
Al clustering gerarchico viene spesso associato un dendogramma, che descrive in che modo i cluster sono stati via via combinati. Tagliando il dendogramma ad un certo livello, i sottoalberi ottenuti rappresentano i cluster prodotti dall'algoritmo in un certo istante di computazione.
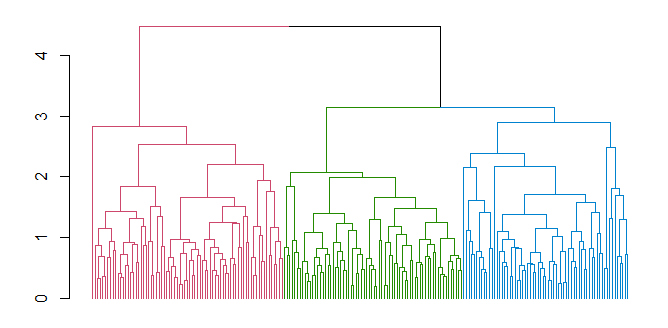
5.2 Criteri di terminazione
Elenchiamo alcuni criteri di terminazione comuni:
- Supponendo di conoscere a priori il numero di cluster da ottenere, si termina l'algoritmo quando si ottiene il numero desiderato.
- Si procede sino a concludere il dendogramma per intero. Ciò è utile in contesti in cui il concetto di distanza riflette il concetto di evoluzione ed il dendogramma descrive rapporti evolutivi (es. nel confronto di genomi di specie diverse).
- Si termina l'algoritmo nel momento in cui la fusione di due cluster produce un cluster inadeguato (es. la distanza media dei punti dei cluster dai rispettivi centroidi cresce troppo, allora i cluster erano lontani tra loro, pur avendo la distanza minima tra tutti ).
5.3 Misure alternative di distanza tra cluster
Altre misure di distanza tra cluster che non includano i centrodi sono le seguenti:
- Single link: la distanza minima tra due punti in due cluster X ed Y.
- Complete link: la distanza massima tra due punti un due cluster X ed Y.
- Average link: la distanza media tra le distanze di tutti i punti di X con tutti i punti di Y.

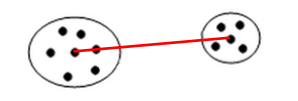
5.3.1 Medoid distance
Un elemento interessante per calcolare la distanza tra cluster potrebbe essere il medoide (o 1-mediana), ovvero il punto del cluster tale che la somma delle distanze degli altri punti del cluster ad esso è minima. A differenza del centroide, il medoide è sempre un punto del cluster. A questo punto, la medoid distance è la distanza tra due cluster X e Y data dalla distanza tra i medoidi di X e Y.
5.4 Complessità del clustering gerarchico
Prendiamo come esempio il seguente pseudo-codice:
clusters = getClusterFromPoints(initialData)
while (terminationCriteria() == True):
# starting point
minimumDistance = calculateDistance(clusters[0], clusters[1])
minCluster_a = clusters[0]
minCluster_b = clusters[1]
# calculate minimimum distance
for currentCluster in clusters:
for iterationCluster in clusters:
tempDistance = calculateDistance(currentCluster, iterationCluster)
if (tempDistance < minimumDistance):
minCluster_a = currentCluster
minCluster_b = iterationCluster
minimumDistance = tempDistance
# add the new cluster
clusters.remove(minCluster_a)
clusters.remove(minCluster_b)
newCluster = createCluster(minCluster_a, minCluster_b)
clusters.append(newCluster)
Ad ogni passo l'algoritmo deve calcolare la distanza tra ogni coppia di cluster e scegliere la coppia migliore da unire. Il passo iniziale ha complessità , i successivi passi dovranno analizzare di volta in volta un cluster in meno, per cui avranno un tempo proporzionale a , ... etc.
Se l'algoritmo procede sino alla fine, dovrà ripetere n passi (iterazioni) prima che si raggiunga un unico grande cluster. Di conseguenza la complessità finale dell'algoritmo è . L'algoritmo risulta quindi poco adatto a clusterizzare grandi quantità di dati.
È possibile ridurre leggermente la complessità dell'algoritmo da a usando le code di priorità. La coda di priorità è una struttura dati che permette di ottenere il minimo in un insieme di valori in tempo costante e consente inserimenti e cancellazioni in tempo .
In tal caso, ad ogni iterazione l'algoritmo:
- Troverà la distanza minima tra cluster in tempo costante e i due cluster relativi
- Eliminerà le distanze relative ai due cluster selezionati dalla coda (max. 2n cancellazioni)
- Creerà un nuovo cluster fondendo i precedenti
- Calcolerà le distanze tra i cluster esistenti ed il nuovo cluster, aggiungendole alla coda (al più n inserimenti)
Sia il passo 2 che il passo 4 hanno complessità . Nonostante le ottimizzazioni, il clustering gerarchico resta inefficiente per grandi quantità di dati.
5.5 Criteri alternativi di combinazione dei cluster
Anziché scegliere i cluster da combinare attraverso la loro distanza minima (indipendentemente da come essa sia misurata), l'algoritmo potrebbe considerare la coppia di cluster tale che il cluster risultante dalla loro unione abbia raggio o diametro minimo. Definiamo raggio e diametro in un cluster:
- Raggio del cluster: distanza massima tra il centroide e un punto del cluster.
- Diametro del cluster: distanza massima tra due punti qualsiasi del cluster.
Raggio e diametro possono essere utilizzati come parametro di controllo per la terminazione dell'algoritmo, attraverso valori di soglia.
5.6 Clustering agglomerativo e divisivo
Gli algoritmi di clustering gerarchici si dividono in due sottogruppi, a seconda dell'approccio utilizzato per effettuare il clustering:
Clustering agglomerativo È la metodologia precedentemente descritta. Ogni punto forma inizialmente un cluster e ad ogni passo l'algoritmo fonde i due cluster più vicini. È chiamato approccio bottom-up.
Clustering divisivo Tutti i punti appartengono inizialmente ad un cluster. Ad ogni passo un cluster viene suddiviso in due cluster più piccoli a seconda di criteri di ottimalità della separazione. È chiamato anche approccio top-down. Valgono le metriche e i criteri visti precedentemente.
5.7 Clustering gerarchico in spazi non euclidei
Negli spazi non euclidei, il concetto di centroide non è definito. In tal caso, si elegge un punto del cluster rappresentate lo stesso, chiamato clusteroide. Quest'ultimo dovrebbe essere scelto come punto <<centrale>> del cluster (es. potrebbe essere il medoide). Le misure di distanza tra i cluster viste nel caso euclideo, così come i criteri di terminazione, restano validi: basta sostituire nelle definizioni, dove presente, il centroide con il clusteroide.
6. Algoritmo K-means
Con il termine K-means si indica una classe di algoritmi di clustering partizionali basati su assegnamenti di punti. Essi permettono di suddividere un insieme di oggetti in k gruppi sulla base dei loro attributi. Lavorano su spazi euclidei e assumono la conoscenza a-priori del numero di cluster k, che costituisce un iperparametro per l'algoritmo. Sono tuttavia presenti alcune tecniche per dedurre il miglior valore di k attraverso una serie di esperimenti.

6.1 Definizione formale
Fissato k, l'algoritmo prende in input un training set di dati : L'obiettivo del k-means è quello di partizionare l'insieme TR in cluster, il cui contenuto risulta più compatto (o denso) possibile. L'output è quindi una partizione esprimibile come segue: Tale che: Definiremo una funzione di assegnamento ai cluster: tale che: Definiremo il centroide del cluster l'elemento medio: Il vincolo secondo il quale i cluster debbano essere compatti è misurato attraverso una funzione costo che, preso in input un determinato partizionamento , calcola la somma della varianza non normalizzata per ogni cluster : Il problema dell'algoritmo k-means sta nel trovare la partizione ottimale che minimizzi la funzione .
6.2 Descrizione dell'algoritmo
L'algoritmo è composto da un primo step di inizializzazione ed un altro step di iterazione. Lo step di iterazione si compone di due sotto step, l'assegnamento e l'aggiornamento.
6.2.1 Inizializzazione
- Si scelgono punti randomici con alta probabilità di finire in cluster differenti
- Si costruiscono cluster i cui centroidi sono i punti selezionati.
6.2.2 Iterazione
- Assegnamento: assegna ogni punto al cluster il cui centroide è più vicino
-
Aggiornamento: calcola la posizione del centroide in ognuno dei cluster
-
Vengono ripetuti i primi due passi sino a che non si soddisfa un criterio di terminazione.
6.2.3 Criterio di terminazione
Uno tra i criteri di terminazione più utilizzati consiste nel terminare l'algoritmo quando la differenza tra i valori della funzione costo, tra due iterazioni consecutive, scende al di sotto di una soglia stabilita, ovvero l'algoritmo tende a stabilizzarsi.
6.3 Scelta dei k centroidi iniziali
Per la scelta iniziale dei k punti si potrebbe effettuare il clustering su un piccolo campione di dati (es. utilizzando il clustering gerarchico), fermarsi non appena si ottengono k cluster e utilizzare i punti più vicini ai rispettivi centroidi come i k punti iniziali. Tale approccio è discretamente buono, ma oneroso computazionalmente.
Un approccio alternativo consiste nel selezionare un punto randomicamente dall'insieme e inserirlo in un insieme . Dopodichè aggiungere ad S il punto che massimizzi la distanza minima di dai punti in :
Ed iterare il processo sinché .
6.4 Scelta del valore di k
In molti casi non conosciamo a priori il numero k di cluster attesi. Tuttavia, k è un parametro richiesto dall'algoritmo di cui non possiamo fare a meno (iperparametro, non determinato dall'algoritmo stesso). Occorre quindi eseguire l'algoritmo per diversi valori di k e prendere quello per cui il clustering ottenuto è migliore.
Per misurare la qualità dei cluster, si può far riferimento alla distanza media dei punti dai rispettivi centroidi. Il clustering ottenuto è buono se la distanza media è bassa. Tuttavia:
- All'aumentare di k la distanza media dei punti dai centroidi diminuisce. Essa potrebbe diminuire a tal punto da partizionare un cluster già omogeneo.
- Al diminuire di k la distanza media dei punti dai centroidi aumenta. Di conseguenza potrebbero non essere rilevati alcuni cluster.
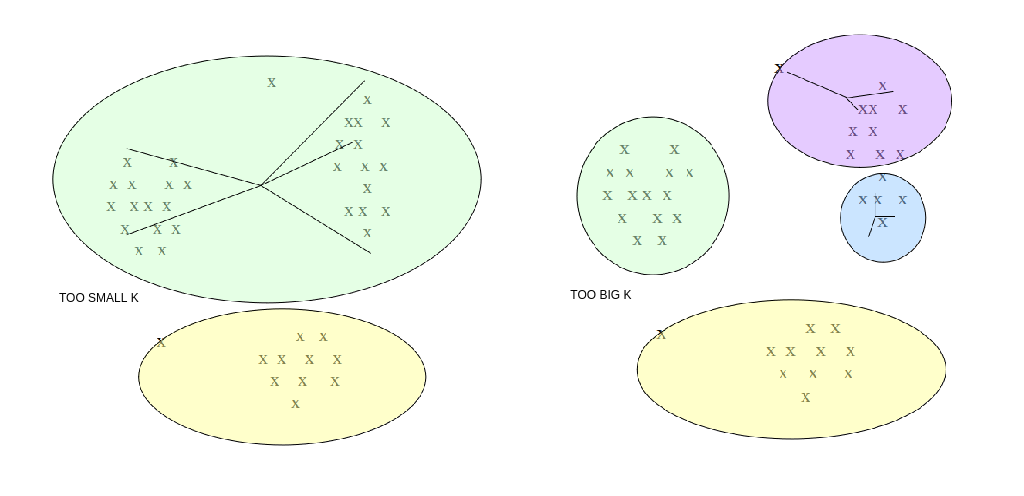
Come determinare il valore ideale di k? Osservando il grafico sottostante notiamo che all'aumentare di k, la distanza media dal centroide diminuisce. Il valore ideale di k risiede nel flesso della curva, dove la variazione rallenta.
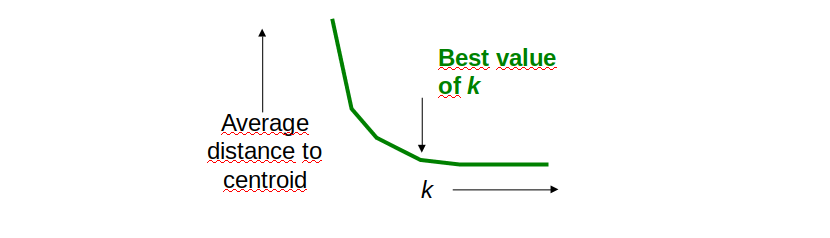
Nella pratica, l'approccio migliore è dato dalla ricerca binaria nello spazio dei valori di k. Supponiamo che tra due valori x e y assunti dal parametro k ci sia una differenza non trascurabile nella distanza media dai centroidi:
- Prendiamo il valore medio ed effettuiamo il clustering per .
- Se il valore della distanza media dai centroidi è vicino a quello per allora poniamo , o viceversa.
- Ripetiamo i passi 1 e 2 sino a quando l'intervallo di ricerca non è sufficientemente piccolo.
6.5 Complessità del k-means
La complessità dell'algoritmo dipende dal numero di iterazioni t e dal numero di cluster k. Generalmente, k e t sono molto più piccoli di n. La complessità risulta essere .
Risulta essere più efficiente del clustering gerarchico, ma:
- Spesso converge ad una soluzione localmente ottimale.
- Non è in grado di trovare cluster con forma non convessa o di dimensioni molto diverse.
- È molto sensibile a rumore e outliers: anche in basse quantità, possono influenzare la posizione del centroide.
- Occorre specificare k (eventualmente ricavandolo attraverso ricerche).
<Da wikipedia> In termini di qualità delle soluzioni l'algoritmo non garantisce il raggiungimento dell'ottimo globale: la qualità della soluzione finale dipende largamente dall'insieme di gruppi iniziale e può, in pratica, ottenere una soluzione ben peggiore dell'ottimo globale. Dato che l'algoritmo è di solito estremamente veloce, è possibile applicarlo più volte e scegliere la soluzione più soddisfacente fra quelle prodotte. Un altro svantaggio dell'algoritmo è che esso richiede di scegliere il numero di gruppi k da identificare; se i dati non sono naturalmente partizionati si ottengono risultati strani. Inoltre, l'algoritmo funziona bene solo quando sono individuabili gruppi sferici nei dati.
6.6 K-means su big data
Per clusterizzare grosse quantità di dati in spazi con elevato numero di dimensioni (che non possono risiedere in memoria principale), si utilizzano opportune varianti del K-means, come gli algoritmi BFR e CURE.
L'algoritmo BFR utilizza una rappresentazione compatta dei cluster, riassunti da un insieme di statistiche e valori, e degli insiemi di punti non ancora assegnati ai cluster, per poter effettuare le operazioni di assegnamento direttamente sulla RAM.
L'algoritmo CURE è un estensione del K-means di base per cluster di qualsiasi forma, in cui ogni cluster è descritto da un insieme di punti rappresentativi, che vengono successivamente utilizzati per raffinare gli assegnamenti.
7. Algoritmo density based (DBSCAN)
Il DBscan (Density-Based Spatial Clustering of Applications with Noise) è un algoritmo di clustering basato su densità. Ogni cluster è visto come una regione di punti connessi con densità sufficientemente alta. Per regione densa si intende una regione contenente un numero di punti sufficientemente elevato in un intorno dello spazio sufficientemente limitato.
Il DBscan richiede due iperparametri:
- il raggio legato alla grandezza dei cluster.
- , che rappresenta il numero minimo di punti che un cluster deve avere.
7.1 Definizione formale
Diamo un paio di definizioni preliminari:
-
Definiamo -intorno di un punto Q l'insieme dei punti a distanza al più da Q.
-
Definiamo P punto direttamente raggiungibile per densità da Q, rispetto a e se:
- P appartiene a
- Q è un core-point, ovvero
-
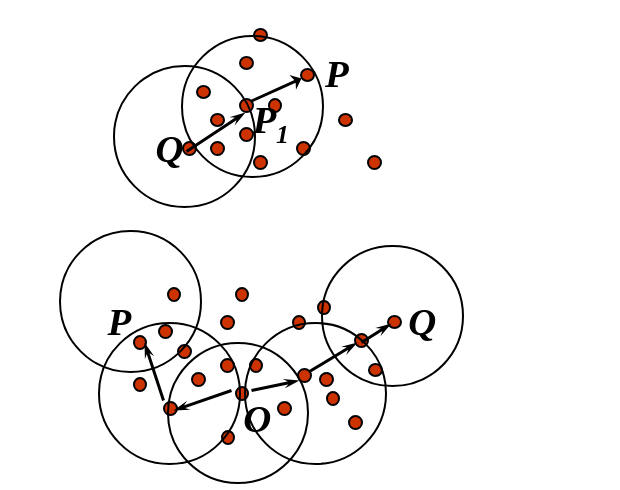
Definiamo P punto raggiungibile per densità da Q, rispetto a e , se e solo se esiste una catena di punti con e tali che sia direttamente raggiungibile per densità da .
-
Definiamo P punto connesso per densità a un punto Q, rispetto a e , se esiste un punto O tale che sia P che Q siano raggiungibili per densità da O, rispetto a e ,
Un cluster in DBscan è definito come un insieme massimale di punti connessi per densità. Formalmente, se D è l'insieme di tutti i punti da clusterizzare, un cluster C, rispetto a e , è un sottoinsieme non vuoto di punti di D tale che:
- se e è raggiungibile per densità da P rispetto a e , allora (Massimalità).
- , P è connesso per densità a Q (Connettività).
7.2 Procedura generale
La procedura generale seguita dal DBSCAN è la seguente:
- Si sceglie un punto random P non ancora visitato.
- Si calcola l'intorno : se è un core point, allora crea un cluster C e va al passo successivo, altrimenti marca P come outlier o rumore e torna al passo 1.
- Aggiunge P e tutti i punti appartenenti a al nuovo cluster C.
- Per ogni punto , aggiunge ricorsivamente tutti i punti appartenenti a , ovvero quei punti raggiungibili per densità da P finché possibile.
- Si ripete il passo 1 sino a che tutti i punti non sono stati visitati.
Al termine della procedura, si formeranno diversi cluster e possibili outlier. I punti inizialmente marcati come outlier potrebbero successivamente entrare a far parte di cluster.
7.3 Scelta dei parametri
La scelta dei parametri è basata su euristiche, generalmente si pone , dove D è la dimensione dello spazio. Per ottenere cluster più significativi, conviene assegnare valori tanto più alti del valore minimo D+1 per quanto:
- Più alto è il dataset di punti
- Maggiore è il rumore presente
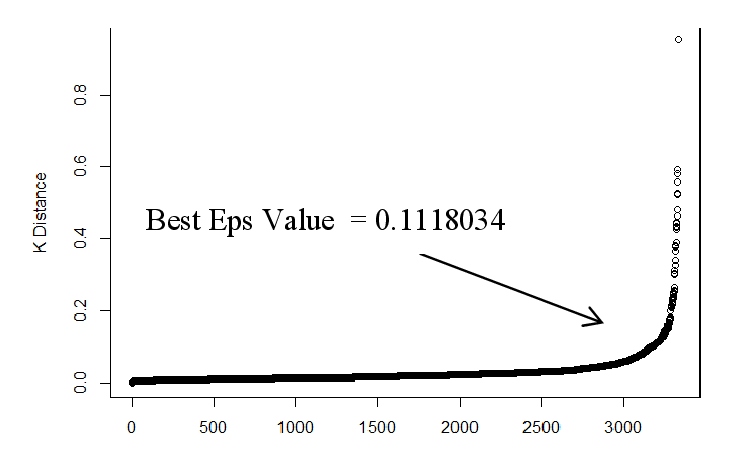
Una volta stimato , si passa a stimare il valore del raggio : per stimare si possono ordinare i punti del dataset sulla base della distanza dal k-esimo elemento più vicino, dalla distanza più alta a quella più bassa e plottare tali distanze ordinate. La curva che si ottiene e simile a quella vista per il clustering gerarchico. Il valore ottimale di è l'ordinata del punto del grafico in cui la curva <<piega>> maggiormente. Scegliendo valori troppo bassi di , molti punti non verrebbro clusterizzati, mentre valori troppo alti porterebbero a cluster troppo grandi.
7.4 Complessità di DBscan
La funzione chiave che determina la complessità di DBscan è quella che calcola l'-intorno di un punto. Con l'utilizzo di strutture indicizzate (es. mappe hash) è possibile ottenere l'-intorno di un punto in tempo . Dal momento che l'-intorno è calcolato una sola volta per ogni punto, la complessità dell'algoritmo è .
7.5 Vantaggi e svantaggi
I vantaggi dell'algoritmo sono i seguenti:
- Non richiede la conoscenza del numero di cluster
- Può trovare cluster di forma arbitraria
- Contempla la nozione di outlier
- L'assegnamento ai cluster è poco influenzato dall'ordine di esaminazione (meno che per i punti di bordo).
Mentre i principali svantaggi sono:
- La determinazione di due iperparametri strettamente dipendenti dal tipo di dato.
- Non è in grado di individuare cluster con notevoli differenze di densità.
8. Coefficiente di Silhouette
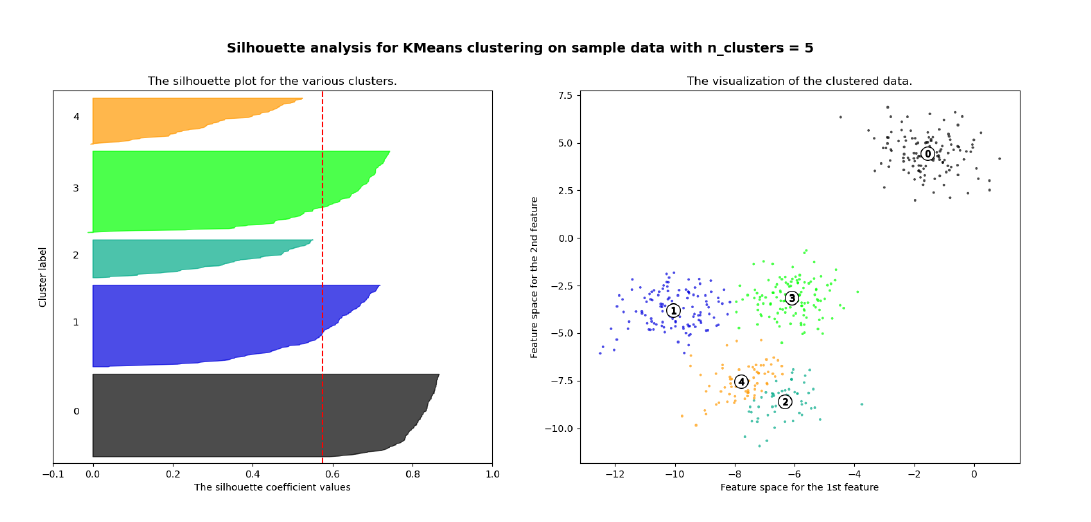
Il coefficiente di Silhouette è una metrica utile per la validazione del clustering effettuato, e quindi per verificare la qualità di un determinato metodo di clustering.
8.1 Calcolo del coefficiente
Per ogni osservazione viene calcolata la distanza media tra tutti i punti appartenenti allo stesso cluster. Dopodiché si calcola la distanza media tra il punto e tutti gli altri cluster e si seleziona il cluster con la distanza media più piccola, chiamata . Il coefficiente di Silhouette è dato dalla seguente formula: Analizziamo i casi:
- indica che l'osservazione è ben clusterizzata. Di fatto il cluster è più lontano rispetto al cluster di appartenenza. Più il valore è vicino ad 1, meglio i dati sono clusterizzati. Si considerano discretamente ottimali valori al di sopra di 0.5.
- indica che l'osservazione è stata posizionata in un cluster sbagliato, di fatto il cluster è mediamente più vicino rispetto al cluster di appartenenza.
- indica che l'osservazione sta a metà tra ed il cluster di appartenenza, per cui comporta un caso dubbio.
Classificazione
1. Introduzione
Nell'asserzione statistica, la classificazione è definita come un problema di identificazione della classe di appartenza di una osservazione, rispetto ad un insieme di classi, sulle basi di un training set contenente osservazioni la cui classi di appartenenza sono note. Nel machine learning, la classificazione è considerata un metodo di apprendimento supervisionato (supervised learning). Essa è un esempio di pattern recognition. Il prodotto di un algoritmo di classificazione è detto modello. Data in input una nuova osservazione, il modello è in grado di assegnare una classe a tale osservazione con un certo grado di accuratezza. Spesso il modello è basato su parametri interni affinati attraverso il training set, e (talvolta) parametri esterni configurati manualmente, chiamati iperparametri.
1.1 Definizione formale
Sia un esempio in input, dove è l'insieme di tutti i possibili esempi utilizzabili dall'algoritmo. Definiamo l'insieme delle possibili classi ed ipotizziamo che appartenga ad una di esse, nello specifico ad . Definiamo un algoritmo di classificazione come una funzione: Il classificatore effettuerà una predizione sulla classe di appartenenza di . Il cappello nella indica che la classe è stata predetta, al contrario di che rappresenta la classe corretta di . Vogliamo che il nostro classificatore predica correttamente la classe, quindi che .
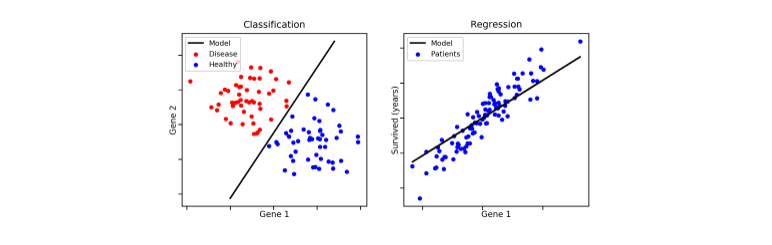
1.2 Classificazione e predizione
Ambo classificazione e predizione sono due metodi di tipo supervised learning. Entrambe utilizzano le feature delle osservazioni per classificare / predire un risultato. È possibile creare confusione tra le due tecniche, per cui evidenziamo la differenza principale: la classificazione predice l'etichetta della classe categoriale di appartenenza (discreta o nominale), mentre la predizione modella funzioni continue e consente la predizione di dati sconosciuti o mancanti.
1.3 Procedimento generale di un classificatore
Lo schema generale per la classificazione si suddivide nella creazione del modello e nell'utilizzo di quest'ultimo. Nella prima fase si utilizza un insieme di tuple, chiamato training set, dove ogni tupla (o osservazione) è caratterizzata da vari attributi (o features) e da una classe di appartenenza. Il modello viene costruito attraverso varie tecniche (alberi decisionali, principi probabilistici o geometrici, etc.) a partire dai dati di training.
- Costruzione del training set
- Scelta del metodo di apprendimento
- Allenamento del modello
Una volta finita la fase di creazione, si applica il modello a dei nuovi dati appartenenti ad un test set e si controlla che le etichette predette corrispondano alle etichette originali: viene quindi misurata la performance del classificatore. Il test set è fortemente indipendente dal training set, al fine di produrre un modello più generico possibile. Se la misura di performance è discretamente alta, allora si utilizza il modello per classificare nuovi dati.
- Si applica il modello al test set
- Si misurano le performance
- Si accetta o rigetta il modello in base ai risultati
1.4 Requisiti dei classificatori o predittori
I requisiti principali di un classificatore o di un predittore sono i seguenti:
- Accuratezza: predire correttamente le etichette delle classi / corretto valore di un attributo
- Velocità, intesa come:
- Tempo impiegato nella costruzione del modello (training time).
- Rapidità con cui il modello performa una classificazione / predizione (classification / prediction time).
- Robustezza: la capacità di manipolare dati con rumore o con feature mancanti.
- Scalabilità: mantenere l'efficienza all'aumentare dei dati, quindi manipolare anche dati in memoria secondaria.
- Interpretabilità dei risultati.
2. Alberi decisionali
Gli alberi decisionali sono uno strumento noto nei campi del machine learning, data mining e della statistica. Ogni nodo interno dell'albero contiene un test su uno o più attributi, tale test stabilisce quale dei sottoalberi deve essere visitato. Un test tipicamente valuta una feature, in tal caso si parla di alberi univariati, o una combinazione di feature, nel caso di alberi multivariati. Ogni foglia contiene una etichetta di classe.
Alcune importanti osservazioni:
- La classe di una osservazione (o tupla) si ottiene seguendo il percorso che va dalla radice dell'albero ad una foglia che determina la classe, sulla base dei test residenti nei nodi interni.
- Ad ogni nodo interno è possibile associare l'insieme delle tuple che soddisfano le condizioni testate partendo dalla radice sino ad arrivare al nodo X.
- La conoscenza rappresentata nell'albero decisionale può essere estratta e rappresentata in forma di regole di produzione if-then. Le regole estratte sono poi utilizzate per la classificazione di nuovi oggetti.
2.1 Esempio esplicativo
Ipotizziamo di avere il seguente training set, dove ogni osservazione è formata da 4 feature: e da tali attributi si decide di giocare una partita di pallone o meno (P = Play, N = Not play). In tal caso il task del classificatore è quello di creare un modello in grado di analizzare le condizioni giornaliere in input e determinare se è il caso di giocare una partita o meno.
| OUTLOOK | Temperature | Humidity | windy | class |
|---|---|---|---|---|
| Sunny | hot | high | false | N |
| Sunny | hot | high | true | N |
| Overcast | hot | high | false | P |
| Rain | mild | high | false | P |
| Rain | cool | normal | false | P |
| Rain | cool | normal | true | N |
| Overcast | cool | normal | true | P |
| Sunny | mild | high | false | N |
| Sunny | cool | normal | false | P |
| Rain | mild | normal | false | P |
| Sunny | mild | normal | true | P |
| Overcast | mild | high | true | P |
| Overcast | hot | normal | false | P |
| Rain | mild | high | true | N |
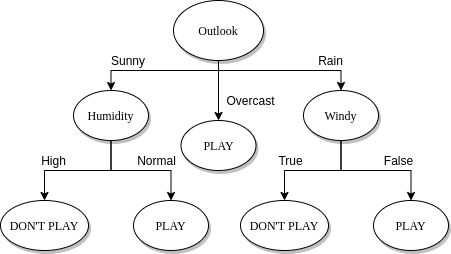
Attraverso un algoritmo di classificazione viene creato un albero decisionale come quello raffigurato nell'immagine sottostante. Più l'albero è bilanciato, più si ridurrà il tempo di classificazione / predizione di una osservazione. Tuttavia, è bene considerare anche il numero di rami uscenti da un nodo interno, poiché molti rami uscenti indicano test computazionalmente costosi. Una production rule tirata fuori da tale albero potrebbe essere la seguente:
if outlook == 'Sunny' and humidity == 'Normal':
return 'PLAY'
2.2 Costruzione di un albero decisionale
Un albero decisionale può essere costruito in maniera top-down. Partendo dalla radice, è possibile applicare una serie di passi ricorsivamente.
- Supponiamo di essere al nodo t.
- Vi sono due possibilità:
- Tutte le tuple associate all'insieme assumono la stessa classe y (quindi t si dice nodo puro) t diventa una foglia di classe y
- Altrimenti il nodo t si definisce impuro e:
- Se è presente un attributo A tra gli attributi ancora non utilizzati:
- Si partiziona sulla base dei valori di A (splitting)
- Si creano tanti figli del noto t quante sono le partizioni create
- Per ciascun figlio si reitera il processo.
- Altrimenti si crea una foglia di classe y, dove la classe y è di maggioranza nell'insieme delle tuple associate al nodo (*).
- Se è presente un attributo A tra gli attributi ancora non utilizzati:
(*) Nel caso di un nodo impuro ed in assenza di ulteriori attributi da utilizzare, è possibile stabilire una distribuzione di probabilità P tale che: per ogni classe C nell'insieme S del nodo, si assegna una probabilità P(C) data dal rapporto di osservazioni di classe C in S su osservazioni totali in S.
2.3 Splitting
Il processo di splitting incontrato nella costruzione dell'albero decisionale va attenzionato in base al tipo di attributo scelto. Consiste nel partizionare l'insieme di tuple S rispetto ad un nodo t in base ai valori che l'attributo può assumere.
Ipotizziamo di trovarci al nodo impuro X con un insieme di osservazioni e di aver scelto un attributo A:
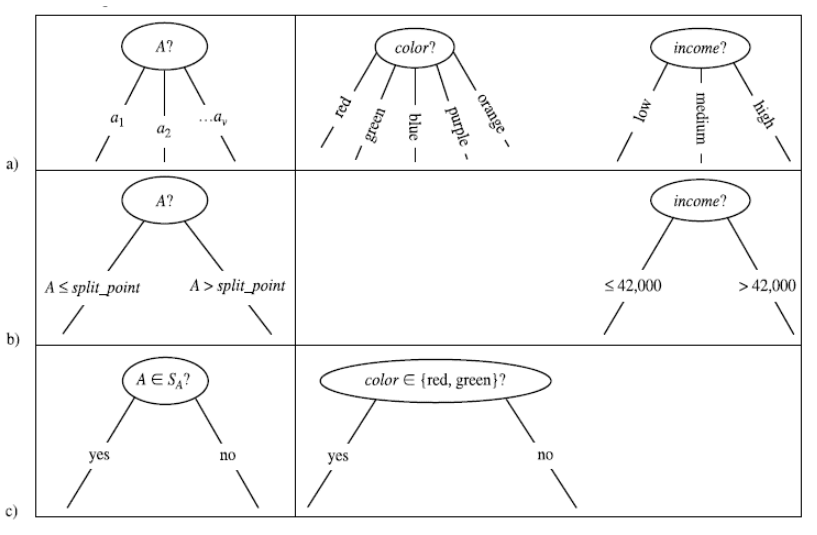
- (a) Se A è un attributo categoriale, allora le osservazioni assumono uno tra i k valori finiti di A. Si formano k nodi figli di X e si partiziona l'insieme in k sottoinsiemi sulla base dei valori di A e si assegnano ai rispettivi nodi figli.
- (b) Se l'attributo è continuo allora si definisce un valore di soglia e si partiziona l'insieme a seconda se o . La soglia è scelta in modo che ogni partizione abbia un numero minimo di elementi. Si aggiungono due figli ad X a cui sono associate rispettivamente le partizioni create.
- (c) Se l'attributo è booleano allora si partiziona in due insiemi e a seconda che oppure . Si aggiungono due figli ad X a cui sono associate rispettivamente le partizioni create.
2.3.1 Scelta degli attributi
La costruzione dell'albero decisionale è fortemente influenzata dall'ordine in cui si considerano gli attributi per lo splitting. Al variare dell'ordine, l'albero in output differisce; l'obiettivo consiste nello scegliere l'albero più semplice e compatto possibile. Nell'immagine che segue troviamo due alberi costruiti a partire dallo stesso training set, con un criterio di scelta degli attributi differente:
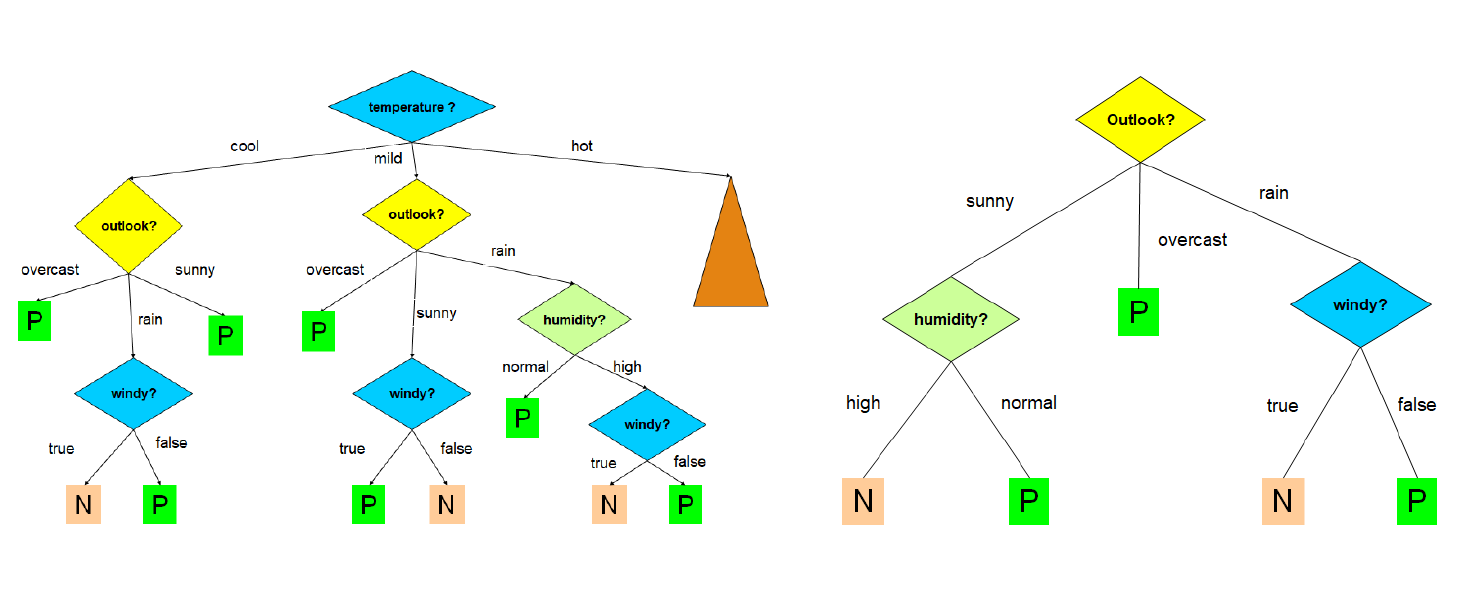
Ovviamente l'albero a destra è più compatto, comprensibile ed efficiente di quello a sinistra. Trovare l'albero minimale (con altezza minore) è un problema NP-Hard, per cui occorre utilizzare degli algoritmi approssimati che cerchino un ottimo locale sfruttando una strategia greedy. Un' euristica ricorrente è la seguente:
Si sceglie ad ogni passo l'attributo che divide le osservazioni in insiemi che sono relativamente puri.
L'obiettivo è quindi quello di effettuare scelte che portino più rapidamente ai nodi foglia. Esistono varie nozioni di purezza che esamineremo in seguito, e prendono il nome di misure di goodness.
2.3.2 Algoritmo greedy ricorsivo
Descriviamo l'algoritmo greedy ricorsivo come segue:
-
Passo base:
- Se tutte le osservazioni in S associato al nodo t assumono la stessa classe, quindi t è un nodo puro, allora si crea una foglia contenente tutti i dati.
- Altrimenti, se non vi sono ulteriori attributi da selezionare per lo splitting, si crea un nodo foglia con l'etichetta di maggioranza.
-
Passo ricorsivo:
- Si seleziona l'attributo A che massimizza una misura di goodness;
- Si effettua lo splitting di S rispetto al nodo t sulla base di A.
- Si applica ricorsivamente l'algoritmo sui figli del nodo t.
build_decision_tree (S, attributes):
if observations in S have the same class:
make a new leaf with this class
else:
if the node is impure but there are no attributes:
make a new leaf with the most frequent class in S
else:
A = attribute that maximize the goodness measurement
partitions = split(S, A)
for partition in partitions:
build an internal node, son of the current node
build_decision_tree(partition, attributes - {A})
2.3.3 Splitting su attributi continui
Nel caso di attributi continui occorre scegliere un valore di soglia, per cui lo splitting effettuato in questo caso dipende anche da questo parametro. Se l'attributo è continuo è necessario quindi calcolare più valori di goodness per lo stesso attributo e prendere come riferimento quello con la goodness più alta. Questo aggiunge un layer di complessità alla scelta degli attributi.
2.4 Misure di goodness
Una misura di goodness quantifica la purezza dei nodi prodotti dallo splitting, scegliendo uno tra gli attributi. Conosciamo tre misure più ricorrenti:
- Information gain (utilizzata nell'algoritmo ID3)
- Gain ratio (utilizzata nell'algoritmo C4.5)
- Gini index (utilizzata nell'algoritmo CART)
2.4.1 Information gain (algoritmo ID3)
La scelta di un attributo mira alla riduzione progressiva dell'entropia. La nozione di purezza è descritta come "quanto un insieme di istanze è prossimo alla situazione ideale", ovvero contenente osservazioni di una sola classe.
- L'entropia massima si ha quando le classi delle osservazioni associate ad un nodo hanno la stessa frequenza.
- L'entropia minima si ha quando tutte le osservazioni associate ad un nodo hanno la stessa classe (nodo puro).
Sia l'insieme delle osservazioni associate ad un nodo X dell'albero, se X è la radice allora è l'intero set di osservazioni. Se X è un nodo interno allora è l'insieme di osservazioni che soddisfano i test imposti dagli archi dell'albero nel percorso effettuato per arrivare dalla radice ad X.
La quantità di informazione è definita nella teoria della informazione come segue: L'entropia, descritta come il grado di incertezza in una distribuzione di probabilità P è definita come segue: Assumiamo di avere solo due classi, P ed N. Ipotizziamo che contenga p osservazioni di classe P ed n osservazioni di classe N. Definiamo la probabilità di una classe in modo frequentista, data quindi dal rapporto di casi favorevoli (osservazioni della data classe in ) su casi possibili (osservazioni in ).
Nel nostro esempio, le classi P ed N hanno rispettivamente probabilità: Per cui l'entropia dell'insieme è così definita: Supponiamo di scegliere l'attributo A come attributo per lo splitting. L'insieme verrà partizionato in insiemi. Supponiamo che l'i-esimo insieme contenga osservazioni di classe P e osservazioni di classe N. Allora l'entropia dell'insieme è data come: Definiamo l'entropia media di rispetto ad A la seguente media pesata delle entropie dei singoli sottoinsiemi : Generalizziamo il concetto e ipotizziamo che in le osservazioni assumano n classi differenti . Allora l'entropia di è data da: Sia A un attributo avente i seguenti valori . Effettuando lo splitting di nei vari a seguito del test su A, l'entropia media di rispetto ad A sarà la media ponderata delle entropie dei singoli sottoinsiemi, ovvero: L'information gain è definito come la riduzione di entropia ottenuta dal partizionamento di scegliendo l'attributo A, ovvero: Ad ogni passo di splitting, l'algoritmo sceglierà l'attributo A che massimizza l'information gain. Ciò equivale a selezionare l'attributo A tale che sia minimo, in quanto è lo stesso (dato il nodo) qualunque sia l'attributo selezionato. Questo approccio minimizza il numero atteso di test necessario per classificare una data tupla. Garantisce inoltre la costruzione di un albero semplice (non necessariamente il più semplice, essendo un approccio greedy).
2.4.2 Svantaggi dell'information gain
L'information gain risulta fortemente sbilanciato in favore dei test che hanno molti esiti. In determinati casi si verifica che un test, che può essere molto discriminante ai fini della divisione dell'albero e quindi con un forte potere predittivo, non venga effettuato perché si basa su un attributo con pochi valori possibili, in favore di un altro test con molti esiti possibilmente poco significativi in termini di predizione.
Ad esempio, se uno degli attributi è un ID, allora ogni partizione sulla base di questo attrbuto avrà una sola tupla. Di conseguenza ogni nodo creato dalla partizione sarà puro e l'entropia media delle partizioni sarà zero, ovvero l'information gain sarà massimo.
2.4.3 Gain ratio (algoritmo C4.5)
Rispetto ad ID3, l'algoritmo C4.5 utilizza una misura di goodness diversa chiamata Gain ratio, che riduce il bias introdotto dall'information gain. Il Gain ratio prende in considerazione il numero e la dimensione delle partizioni ottenute scegliendo un attributo, senza considerare informazioni specifiche sulle singole classi.
Le potenziali informazioni sullo split generato da un attributo A sono rappresentate dallo : Il Gain ratio è dato da: Attributi che determinano molte partizioni con pochi elementi avranno un valore di maggiore, quindi un minore .
2.4.4 Gini index (algoritmo CART)
Il Gini index, anche chiamato Gini impurity, misura l'impurità di un insieme di osservazioni associato ad un nodo dell'albero decisionale. Consideriamo una classe ed una tupla x di classe scelta a caso dal dataset T. Supponiamo di assegnare casualmente ad x una classe sulla base della distribuzione delle frequenze delle classi nel dataset. Il Gini index misura, per ogni classe, la probabilità che . Chiamiamo la probabilità di scegliere una osservazione del dataset di classe , la probabilità di scegliere una classe diversa da a partire dalla distribuzione delle frequenze delle classi è:
Supponiamo di avere n classi, il gini index calcola l'impurità di un nodo sommando, per ogni classe con , la probabilità che si scelga una classe errata (ovvero ). Tale valore viene bilanciato attraverso la probabilità : Dunque, dato un insieme di osservazioni con n classi, il Gini index è definito come segue: Dove è la frequenza relativa della classe in .
Supponiamo che, scegliendo un attributo A per lo split, l'insieme venga partizionato in k sottoinsiemi . Il Gini index dello split è definito come segue: L'attributo A che minimizza è selezionato come attributo di splitting.
2.5 Pruning
L'elevato numero di attributi in un training set o la particolare distribuzione dei valori degli attributi può far crescere notevolmente la dimensione di un albero. Ciò può portare alla costruzione di un modello più complesso, fatto "su misura" sul training set, ma non in grado di classificare correttamente nuovi dati. Questo fenomeno è chiamato overfitting. Rende più difficile la classificazione (dovuto ad outliers) ed è associato ad un aumento non giustificato di errori. Per evitare questo, gli algoritmi di classificazione effettuano un pruning (potatura).
Il pruning consiste nel rimuovere i rami che non contribuiscono ad una corretta classificazione, producendo qualcosa di meno complesso e più comprensibile. Il pruning deve essere fatto senza aumentare eccessivamente il tasso di errore di classificazione del modello.
2.5.1 Pre-pruning e post-pruning
Vi sono varie tipologie di pruning:
- Pre-pruning: è attivato in fase di costruzione dell'albero, nel momento in cui si decide se dividere ulteriormente o meno un determinato sottoinsieme. Fissato un valore di soglia (threshold) t, i rami per cui si ottiene un gain inferiore a t vengono troncati. In alternativa, possono essere utilizzati metodi statistici per effettuare il troncamento.
- Post-pruning: questa tipologia di pruning è utilizzata dagli algoritmi CART e C4.5. Si rimuovono rami e nodi a costruzione dell'albero già avvenuta, sostituendo un intero sotto-albero con una foglia.
Il post pruning, sebbene più dispendioso, consente una analisi più approfondita delle partizioni producendo un albero più realistico. Il C4.5 utilizza un algoritmo di post-pruning chiamato pessimistic pruning o reduced error pruning. Il CART utilizza un algoritmo di post-pruning chiamato cost-complexity pruning.
2.5.2 Pessimistic pruning
Dato un sottoalbero T di radice X, definiamo l'error rate (tasso di errore) atteso di T il numero di osservazioni di che sono classificate in maniera errata. Una strategia semplice di pruning consiste nel potare un sottoalbero in funzione della variazione di error rate predetto che porterebbe all'intero albero. Se tale variazione è positiva, ovvero il tasso di errore aumenta in presenza del sottoalbero, allora il sottoalbero stesso può essere potato e sostituito con una foglia.
Il pruning pessimistico si basa sul calcolo di questa variazione di errore ed è chiamato pessimistico poiché sovrastima leggermente (di una quantità ) il tasso di errore atteso in ogni sottoalbero.
Vediamo la procedura generale:
- Calcoliamo una stima pessimistica dell'error rate atteso sul training set prima di fare lo splitting di un nodo X su un attributo A, considerando il nodo X come una foglia con l'etichetta di maggioranza nel sottoalbero.
Avendo considerato la classe di maggioranza c sostitutiva al sottoalbero, l'error rate sarà calcolato come segue: La stima pessimistica è calcolata aggiungendo un fattore :
- Calcoliamo una stima pessimistica dell'error rate atteso dopo aver eseguito lo splitting di X su A, utilizzando quindi il sottoalbero.
Essendovi uno splitting del nodo X, vi saranno k sottoinsiemi di : . Calcoliamo l'error rate, considerato il sottoalbero, come segue: La stima pessimistica è calcolata aggiungendo un fattore :
- Se allora:
- Viene sostituito il sottoalbero radicato in X con un nodo foglia.
- Viene assegnata ad X l'etichetta di maggioranza tra le foglie del vecchio sottoalbero.
Vediamo un esempio di pruning pessimistico:

2.5.3 Cost complexity pruning
L'algoritmo CART utilizza un algoritmo di post pruning chiamato Cost Complexity pruning. Tale algoritmo costruisce iterativamente m alberi decisionali , dove l'albero decisionale completo e è l'albero formato dalla sola radice.
Alla i-esima iterazione, l'albero è ottenuto a partire dall'albero rimuovendo un sottoalbero t di e sostituendolo con un nodo foglia con associata etichetta di maggioranza ( o distribuzione delle classi). Se è l'error rate atteso per il sottoalbero , il sottoalbero da rimuovere in questa iterazione è quello tale da minimizzare la seguente funzione: Dove è l'albero ottenuto rimuovendo da il sottoalbero , mentre con intendiamo genericamente il numero di foglie in un albero. Uno dei vantaggi di tale algoritmo è che non è necessario stimare un parametro .
2.6 Estrazione di regole da un albero decisionale
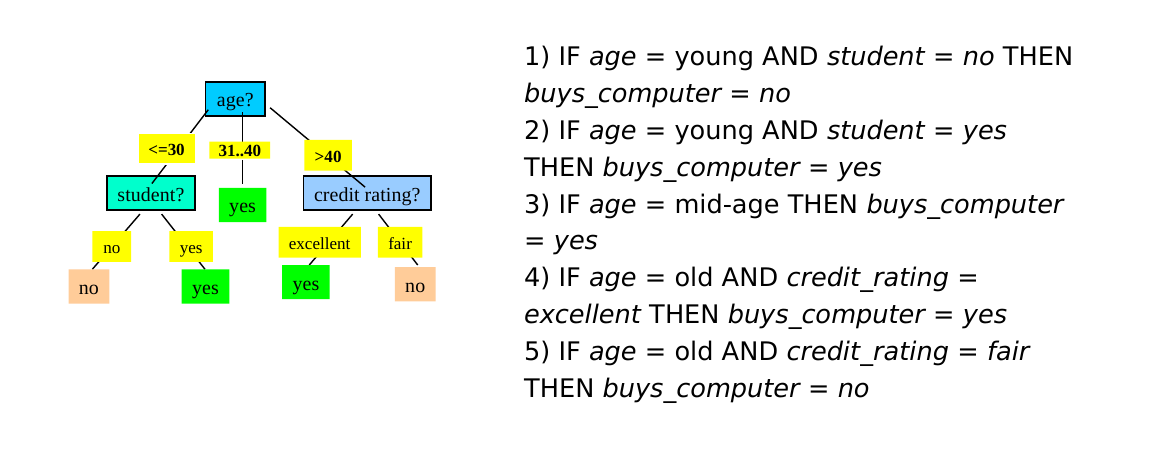
A partire dall'albero decisionale è possibile estrarre delle production rules del tipo IF (condizione) THEN (etichetta). Esiste una regola per ogni cammino che porta dalla radice ad una foglia. Le coppie (attributo, valore) lungo un percorso entrano a far parte della condizione della regola, legate attraverso congiunzione (AND). Il valore contenuto nella foglia determina la predizione finale della classe. Le regole sono mutuamente esclusive ed esaustive.
Vediamo un esempio:
2.6.1 Qualità di una regola
Per stabilire la qualità di una regola per una classe C si utilizzano due misure:
- Copertura (coverage): numero relativo di osservazioni coperte dalla regola, ovvero che soddisfano le condizioni della regola.
- Accuratezza (accuracy): numero relativo di osservazioni di classe C coperte dalla regola.
Una buona regola dovrebbe avere alta coverage per una specifica classe C (ovvero coprire quante più tuple di classe C) ed elevata accuratezza (ovvero classificare bene la maggior parte delle osservazioni di classe C coperte).
Definiamo gli esempi positivi come le osservazioni di classe C coperte dalla regola, mentre gli esempi negativi come le tuple di classe diversa da C coperte dalla regola.
2.6.2 Risoluzione dei conflitti
Idealmente, ogni regola sulla classe C dovrebbe coprire insiemi di osservazioni differenti. Tuttavia, è possibile avere ridondanze o conflitti con due o più regole che coprono più o meno lo stesso insieme di osservazioni. Occorre risolvere un problema di minimal set covering, ovvero trovare il più piccolo insieme di regole sulla classe C che coprono gli esempi positivi. Ciò deve essere fatto producendo regole che abbiano un livello sufficientemente alto di accuratezza.
Alcuni algoritmi noti per la ricerca del minimal set covering sono FOIL, AQ, CN2, RIPPER. Le regole vengono costruite in maniera sequenziale. L'obiettivo è individuare una regola per una classe C che copra molte tuple di classe C (esempi positivi) e nessuna (o poche) tuple delle altre classi (esempi negativi). Lo schema generale è il seguente:
- Sia S il set formato da tutte le osservazioni del training set.
- Le regole vengono apprese una per volta seguendo un criterio greedy basato sulla qualità della soluzione.
- Ogni volta che una nuova regola viene appresa, gli esempi positivi vengono rimossi da S.
- Il processo viene ripetuto sino a quando S non diventa vuoto.
2.6.3 Algoritmi FOIL e RIPPER
Gli algoritmi FOIL e RIPPER utilizzano una strategia greedy e depth-first per generare la regola da aggiungere ad ogni passo.
Sia C la classe; partiamo dalla radice dell'albero decisionale e consideriamo la regola più generale per ottenere la classe C, ovvero quella senza condizioni: Da tale regola otterremo il massimo punteggio di copertura (coverage) poiché tutte le osservazioni rispettano tale condizione, ma anche una pessima accuratezza (accuracy), ovvero saranno incluse anche tutte le osservazioni di classe diversa da C, quindi molti esempi negativi.
Dopodiché si scenderà lungo l'albero scegliendo la condizione che mantenga una ampia copertura e ottimizzi la accuratezza per la classe C. Inevitabilmente, durante l'aggregazione di nuove condizioni scenderanno sia gli esempi positivi che gli esempi negativi della classe C, la scelta va ponderata in base al miglior rapporto (che enfatizza la diminuzione degli esempi negativi, mentre scoraggia quella dei positivi).
Vi è la necessità di introdurre una metrica che diriga l'algoritmo nell'effettuare la scelta migliore. Nel caso dell'algoritmo FOIL si introduce il FOIL gain: le condizioni vengono aggiunte sino a quando la regola ottenuta mantiene un livello di qualità superiore ad una certa soglia, sulla base del FOIL gain.
2.6.4 FOIL gain
Siano e rispettivamente il numero di esempi positivi e negativi ottenuti prima della costruzione della regola. Siano e rispettivamente il numero di esempi positivi e negativi ottenuti dopo della costruzione della regola. Il FOIL gain cerca quindi di favorire regole che hanno alta accuratezza e coprono molti esempi positivi.
3. Classificatori generativi
I classificatori generativi (o classificatori Bayesiani) producono un modello probabilistico traendo informazioni dai dati e predicono la classe di appartenenza più probabile per un nuovo dato a partire dal modello sviluppato. Esempi di classificatori generativi sono le Bayesian networks ed i Gaussian Mixture Models, entrambi basati sul teorema di Bayes.
3.1 Teorema di Bayes
Consideriamo un insieme di alternative che partizionano lo spazio degli eventi . Si trova la seguente espressione per la probabilità condizionata: Dove:
- è la probabilità a priori o probabilità marginale (nessuna informazione su ).
- è la probabilità a posteriori, dato che deriva dal valore di .
- è la verosimiglianza (likelihood).
- è l'evidenza, che funge da costante di normalizzazione.
3.2 Maximum a Posteriori (MAP)
Consideriamo l'evento stocastico " è di classe " dove è una osservazione d'esempio e è una delle possibili classi nel problema di classificazione. Consideriamo la probabilità che risponda alla domanda "qual è la probabilità che si osservi la classe , data l'osservazione ?". Se quantifichiamo tale probabilità per ogni classe tra le esistenti, abbiamo una distribuzione di probabilità condizionata sulle classi, dato l'input . Risulta naturale attribuire all'input la classe che massimizzi la distribuzione di probabilità condizionata: Ricollegandoci al teorema di Bayes, la probabilità da massimizzare è chiamata probabilità a posteriori, da cui il nome del metodo di classificazione: Maximum A Posteriori (MAP). Sostituiamo con la formula precedente: Dal momento in cui l'evidenza costituisce una costante di normalizzazione, massimizzare tale espressione equivale a massimizzare la seguente:
3.2.1 Calcolo delle probabilità
La semplificazione del metodo Maximum a Posteriori attraverso l'utilizzo del teorema di Bayes ci permette di passare da una stima altamente complessa di a due stime relativamente semplici, quali la probabilità a priori e la likelihood.
Calcolo della probabilità a priori
Data una classe , il calcolo della probabilità a priori è relativamente semplice. È sufficiente calcolare in maniera frequentista il rapporto di osservazioni nel dataset facenti parte della classe rispetto alle osservcazioni totali:
P(C) = \frac {\text{#obs. of class C}} {\text{#obs.}}
Calcolo della likelihood
La likelihood è più semplice da stimare rispetto alla probabilità a posteriori poiché il termine condizionante è discreto e finito. Per ogni classe consideriamo la variabile aleatoria composta da sole le osservazioni di classe , quindi è un sottoinsieme di . La probabilità .
Per semplicità consideriamo univariata e distinguiamo due casi:
- è discreta e finita, allora è possibile calcolare la probabilità in maniera frequentista.
- è continua o discreta ma non finita, allora utilizziamo una distribuzione di probabilità nota.
3.2.2 Esempio discreto
Consideriamo una versione semplificata della classificazione degli Iris di Fisher dove troviamo due sole variabili: SepalWidth e SepalLength. Le variabili sono discrete e finite e possono assumere 3 soli valori: small, medium e large, rispetto alla dimensione del sepalo. Sia una variabile aleatoria bidimensionale. L'esempio può appartenere a una tra le classi Setosa, Virginica e Versicolor. Definiamo 3 diverse verosimiglianze , e a partire dalle seguenti tabelle:
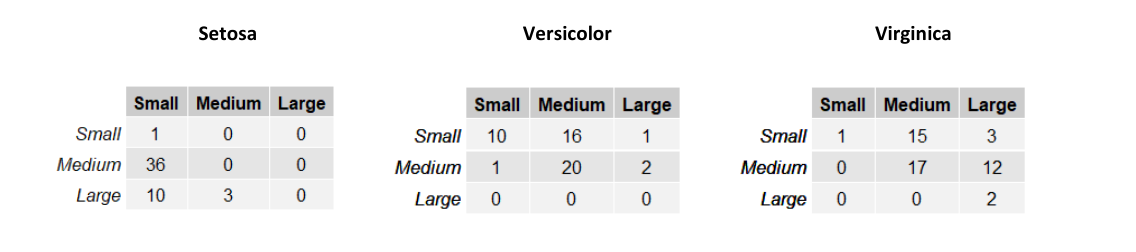
Le righe nelle tabelle rappresentano la larghezza del sepalo (SepalWidth) mentre le colonne la lunghezza (SepalLength). Ogni tabella contiene la frequenza assoluta delle occorrenze per ognuna delle possibili combinazioni delle due variabili. Possiamo trasformare queste tabelle in una distribuzione di probabilità dividendo ogni elemento per il totale delle osservazioni del sottoinsieme considerato.
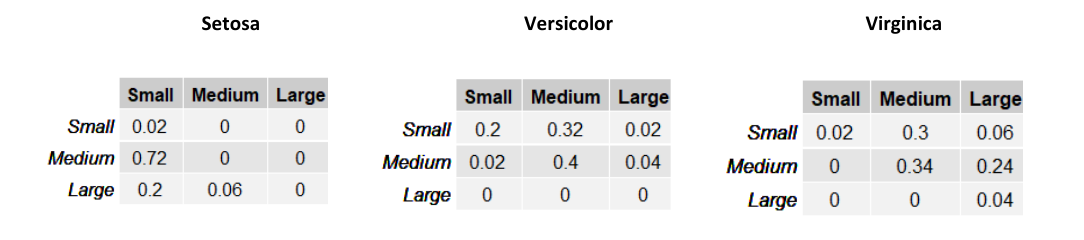
Supponiamo di assegnare una probabilità a priori equa di ad ognuna delle tre classi e stimiamo la classe di un esempio . Per il metodo Maximum a Priori, è necessario prendere in considerazione la classe che massimizzi . Quindi calcoliamo per ognuna delle 3 classi tale espressione:
Classificheremo l'esempio come Versicolor, dato che tale classe massimizza la probabilità a posteriori.
3.2.3 Esempio continuo
Supponiamo di voler classificare il genere di una persona (uomo, donna) in base alla sua altezza ed al suo peso . Supponiamo che se il soggetto è una donna, mentre se il soggetto è un uomo. Introduciamo la variabile aleatoria .
Ipotizziamo che il dataset di esempi sia bilanciato e che quindi le probabilità a priori siano per ognuna delle due classi. Adesso è necessario calcolare la likelihood per entrambe le classi, ma le variabili sono continue, per cui non è possibile costruire una tabella.
Consideriamo il seguente grafico che mostra la distribuzione degli input di sesso femminile () in base ad altezza e peso:

La distribuzione è molto simile ad una gaussiana bidimensionale. Possiamo modellare considerando tutti e soli gli esempi di sesso femminile e calcolando i parametri della gaussiana bidimensionale: Siano gli input di sesso femminile, calcoliamo i parametri della gaussiana bidimensionale:
Facciamo lo stesso considerando solo gli input di sesso maschile e calcoliamo le rispettive likelihood come segue:
- ;
- ;
Classificheremo l'esempio come femmina se , maschio altrimenti.
3.3 Classificatore Naïve Bayes
Il calcolo della likelihood potrebbe essere oneroso nel caso la variabile abbia molte dimensioni. Il classificatore Naïve Bayes assume in maniera naïve che gli attributi di siano condizionalmente indipendenti tra loro, ovvero indipendenti fissata la classe di appartenenza: Tale assunzione è spesso non vera, ma semplifica notevolmente il calcolo e procura generalmente buoni risultati. Per le proprietà di indipendenza condizionata possiamo riscrivere la likelihood come segue: E la regola di classificazione MAP: I singoli termini sono semplici da stimare dato che è monodimensionale. Nella pratica viene scelta una distribuzione tra la Gaussiana e la Multinomiale per modellare approssimare la distribuzione reale dei dati. Se viene utilizzata la distribuzione gaussiana, allora il classificatore prende il nome di "Gaussian Naïve Bayes", mentre nel caso della multinomiale "Multinomial Naïve Bayes".
3.3.1 Gaussian Naïve Bayes
Consideriamo nuovamente la classificazione dei sessi basata su altezza e peso (esempio 3.2.3). Se i dati assumono approssimatamente una distribuzione gaussiana e considerando la assunzione naïve, le probabilità ed possono essere modellate singolarmente attraverso una gaussiana monodimensionale. Eseguiamo il calcolo per ognuna delle classi, ottenendo 4 espressioni più semplici da calcolare:
Dopodiché classificheremo l'esempio come femmina (1) se: maschio altrimenti.
3.3.2 Multinomial Naïve Bayes
Nell'esempio precedente si è fatto uso di variabili aleatorie continue, per cui è necessario considerare una PDF (Probability Density Function) come una distribuzione gaussiana. Quando gli attributi dei dati sono discreti, ha senso utilizzare una PMF (Probability Mass Function).
La distribuzione multinomiale di parametri con , descrive la probabilità per ogni -upla con di assumere i risultati in prove indipendenti, ognuna delle quali ha probabilità di fornire .
Consideriamo l'esempio della text classification. Ipotizziamo di rappresentare un documento d'esempio con la rappresentazione Bag of Words (conteggio delle occorrenze di parole in un vocabolario). Dato un vocabolario di lunghezza , ogni input avrà attributi , con che rappresenta il numero di occorrenze nel documento della -esima parola nel vocabolario.
La likelihood di un esempio sarà . Utilizzando l'assunzione naïve diciamo che il numero di occorrenze della -esima parola nel documento di classe è indipendente dal numero di occorrenze della parola -esima. Possiamo utilizzare la distribuzione multinomiale per calcolare la probabilità , ma è necessario fissare alcuni parametri:
- Il numero di esperimenti sarà il numero totale di parole nel documento
- rappresenta le occorrenze delle parole nel vocabolario in un documento
- La probabilità sarà la probabilità di trovare la parola -esima del vocabolario fissata una classe
È possibile calcolare la probabilità in maniera frequentista: Dove denota le parentesi di Iverson, che valgono 1 se la condizione all'interno è soddisfatta, 0 altrimenti. La probabilità corrisponde al numero di occorrenze della parola -esima in tutti i documenti di classe rispetto al numero totale di parole nei documenti di classe .
È possibile risolvere il problema di classificazione con il metodo MAP: Sostituendo la likelihood con la formula analitica della distribuzione multinomiale: Il rapporto è analogo qualunque sia la classe considerata, per cui massimizzare tale espressione equivale a massimizzare:
3.3.3 Zero probability e underflow
Il metodo Naive Bayes richiede che le probabilità condizionali siano diverse da 0, altrimenti la likelihood risulterà nulla. Inoltre, se le probabilità condizionali sono molto piccole, un prodotto di tante quantità prossime allo 0 può portare problemi di precisione e di underflow.
Per ovviare al primo problema, si può utilizzare la correzione Laplaciana, ovvero aggiungere 1 ad ogni probabilità condizionale.
Per ovviare a entrambi i problemi, si può considerare il log-likelihood, ovvero il logaritmo di , che si traduce in una somma anziché un prodotto dei termini:
3.3.4 Conclusioni
Il classificatore Naive Bayes è facile da implementare, discretamente veloce nella classificazione e produce buoni risultati. Tuttavia, l'assunzione naive non è sempre vera e può provocare una perdita di accuratezza. Le dipendenze tra più attributi, sempre a causa dell'assunzione, non possono essere modellate.
4. Classificatori discriminativi
4.1 Introduzione
I classificatori discriminativi cercano di predire la classe direttamente a partire dai dati osservati, facendo poche assunzioni sulla loro distribuzione. Esempi di classificatori discriminativi sono il Perceptron ed SVM.
4.1.1 Differenze tra generativo e discriminativo
Il classificatore generativo sviluppa un modello probabilistico sui dati a partire da un insieme di assunzioni e predice la classe più probabile per un nuovo dato. Il classificatore discriminativo costruisce una funzione di decisione a partire dai dati osservati stimando pesi calcolati per ogni attributo e dipendenti dai valori dell'attributo stesso. Se è un nuovo dato, si calcola ed il valore ottenuto è la classe di .
4.1.2 Vantaggi e svantaggi
Vantaggi dei classificatori discriminativi:
- Maggiore accuratezza in generale
- Robusti in presenza di errori nel training set
- Facile calcolo del valore della funzione di decisione su un nuovo dato
Svantaggi:
- Tempo di addestramento lungo
- Difficile interpretare i pesi della funzione di decisione calcolata
- Non è semplice incorporare conoscenza a priori (nei metodi Bayesiani risulta molto semplice)
Si rimedia alla difficile interpretazione dei pesi attraverso la explainable artificial intelligence, ovvero tutta una serie di metodi per rendere il risultato di una soluzione comprendibile dagli umani.
4.2 Classificazione lineare vs non lineare
Nella classificazione lineare la classificazione di una osservazione è basata sul valore di una funzione lineare , ovvero una combinazione lineare degli attributi di : Dove sono i pesi della combinazione lineare.
Nella classificazione non lineare la classificazione di è effettuata utilizzando una funzione non lineare degli attributi di X, ovvero dove gli attributi possono assumere potenze diverse dalla prima.
4.2.1 Esempio: lineare binaria vs non lineare binaria
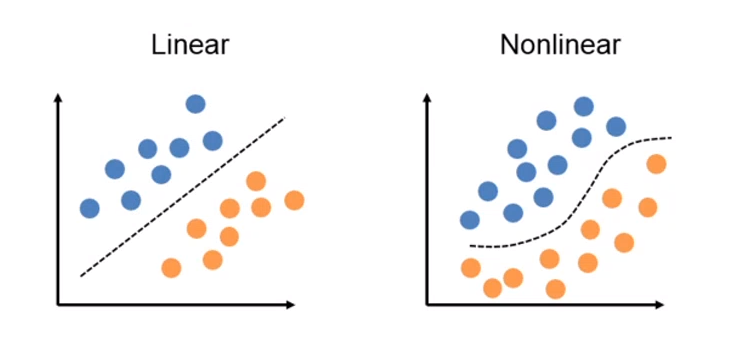
Nella classificazione binaria le osservazioni possono essere separate in due classi differenti. Utilizzare la classificazione lineare binaria si traduce nel trovare un iperpiano separatore che possa suddividere le osservazioni nelle due classi. Si utilizza una classificazione non binaria quando non esiste una funzione lineare in grado di separare tali dati.
4.3 Perceptron
Perceptron è un algoritmo di classificazione lineare binaria. La classificazione viene effettuata sulla base di una funzione predittiva lineare che si ottiene combinando un insieme di pesi con il vettore degli attributi dell'oggetto. In generale, l'algoritmo perceptron è utilizzabile solo quando il dataset risulta separabile linearmente.
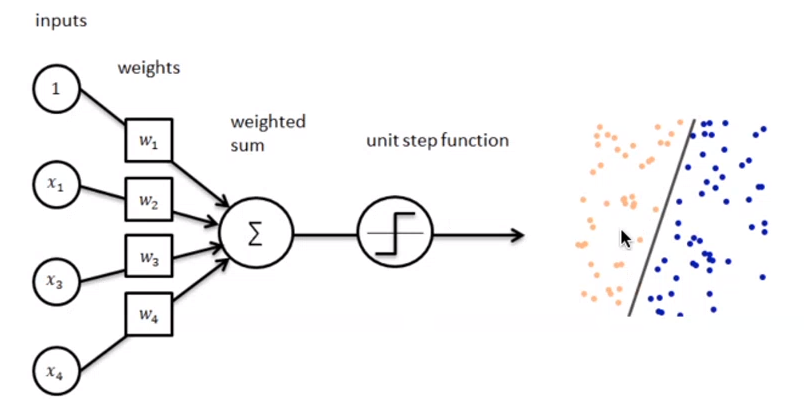
Supponiamo di avere due classi , data l'osservazione , la funzione predittiva è: con w vettore di pesi con cardinalità pari a quella degli attributi + 1. Perceptron effettua un apprendimento online: gli elementi del training set vengono processati uno per volta e i pesi aggiornati ogni volta che un nuovo elemento è preso in esame. Il modello prodotto, chiamato anche single-layer Perceptron, è una rete neurale single-layer. Esistono anche multi-layer Perceptron, che combinano più funzioni di aggregazione.
4.3.1 Definizioni preliminari
Introduciamo alcune notazioni:
- Sia il training set, con una tupla e la rispettiva classe (0 o 1).
- Sia il learning rate, un valore tra 0 e 1 che determina la grandezza della variazione dei pesi ad ogni passo, è un iperparametro.
- Sia la classe di output predetta dal perceptron (0 o 1) per la j-esima tupla del training set D.
- rappresenta l' i-esimo attributo della j-esima tupla del training set D.
- Si pone convenzionalmente (l'attributo di indice 0).
- Sia il peso della i-esima feature al passo t.
Dal momento che , allora equivale alla costante b nell'espressione .
4.3.2 Procedura
Supponiamo che ogni tupla del dataset abbia k attributi, l'algoritmo Perceptron esegue i seguenti passaggi
-
(1) Inizializza i pesi al valore 0 o ad un valore random piccolo.
-
(2) Per ogni coppia :
- (2.1) Calcola l'output attuale:
- (2.2) Aggiorna ognuno dei pesi :
-
(3) Nel caso di learning offline, ripeti il passo n.2 sino a quando l'errore medio di classificazione è inferiore ad una soglia , oppure un numero predefinito di iterazioni è stato completato.
N.B. L'errore medio di classificazione è ottenuto attraverso la seguente formula: Nella pratica, il passo 2 viene iterato affinché la retta (o in generale, l'iperpiano) trovi i coefficienti adatti a separare l'intero dataset in due classi distinte. Ipotizziamo che al tempo t vi sia un errore, l'aggiornamento dei pesi ridefinirà ognuno dei pesi (da utilizzare al prossimo passo ) come segue: Dove:
- è la componente j-esima del vettore dei pesi al tempo t
- sarà nullo nel caso in cui la classificazione sia corretta, -1 nel caso in cui il punto sta al di sotto della retta (o dell'iperpiano), 1 nel caso in cui sia al di sopra.
- è la j-esima componente del punto , classificato al tempo t.
- r è il learning rate, che a seconda della grandezza definisce con quale velocità la retta (o l'iperpiano) converge alla posizione ideale. Tuttavia, un learning rate alto potrebbe causare più errori durante il procedimento.
5. Support Vectors machines
5.1 Idea generale
Il metodo Support Vectors Machines è un metodo di classificazione binaria, ovvero le osservazioni sono classificate in due sole classi. Se i dati del training set sono linearmente separabili, allora l'SVM trova l'iperpiano separatore ottimale, ovvero quell'iperpiano che li separi al meglio. Se i dati non sono linearmente separabili, allora essi vengono prima trasferiti in uno spazio con un numero di dimensioni maggiore, attraverso una operazione di mapping. Con l'aumentare delle dimensioni aumenta anche il volume dello spazio e, di conseguenza, i dati tendono a separarsi maggiormente, per cui è molto più probabile che diventino linearmente separabili. Si può dimostrare che per ogni insieme di dati esiste uno spazio con un numero di dimensioni sufficientemente grande tale che i dati siano linearmente separabili. Una volta eseguito il mapping, SVM procede trovando l'iperpiano separatore ottimale.
5.2 Iperpiano ottimale e vettori di supporto
Definiamo i vettori di supporto (support vectors) come le osservazioni più vicine all'iperpiano separatore. Tali osservazioni sono le più complesse da classificare; in generale più un punto è lontano dall'iperpiano separatore, più è certa la appartenenza alla classe.
I vettori di supporto servono a stabilire quale tra gli iperpiani che separano linearmente i punti è quello ottimale. Introduciamo i margini come le distanze tra questi vettori di supporto e l'iperpiano. L'iperpiano separatore ottimale è quello che massimizza i margini.
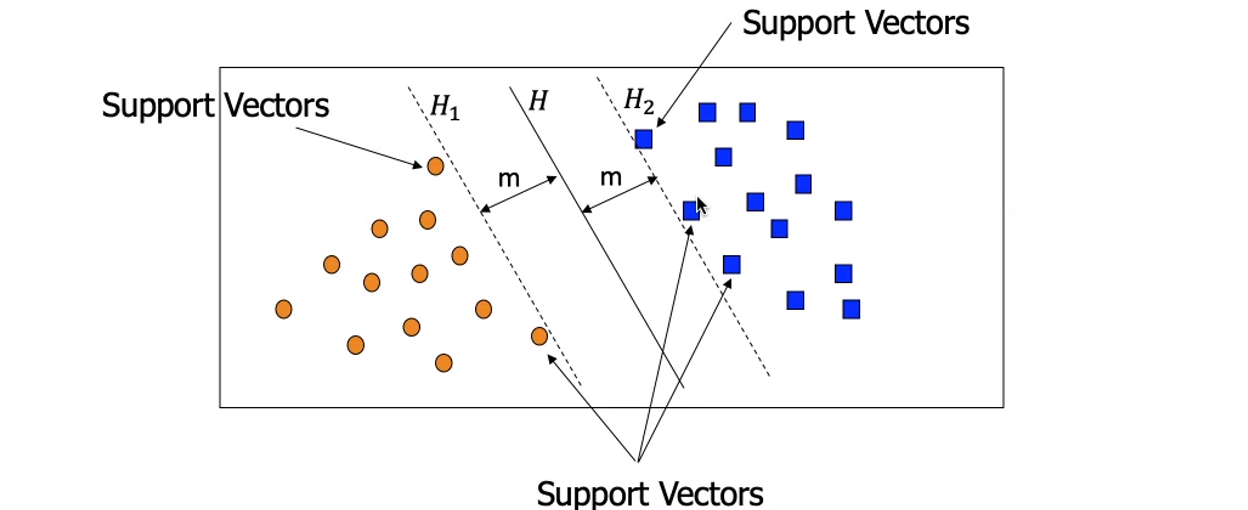
5.3 Condizioni sui punti
Possiamo rappresentare un iperpiano a dimensioni con la seguente equazione:
Dove con si intende il prodotto scalare tra un vettore dei pesi e delle incognite , e è uno scalare detto bias. Essendovi due classi, possiamo stabilire la classe di una osservazione a seconda che stia sopra o sotto l'iperpiano. Sia una osservazione, allora:
Tuttavia, utilizzando solo questa condizione andrebbe bene qualsiasi iperpiano che separi le due classi. Imponiamo invece che ogni punto al di sopra dell'iperpiano rispetti la seguente condizione:
Simmetricamente, per i punti al di sotto dell'iperpiano:
Se un punto rappresenta un vettore di supporto, ovvero risiede nella frontiera della separazione, allora:
Risulta scomodo dover considerare due condizioni (1, 2) da applicare ai punti. È possibile ridurre entrambe le espressioni ad una sola espressione, introducendo la variabile come segue:
Le condizioni vengono ridotte alla seguente espressione:
O anche:
Esempio: consideriamo un punto al di sotto dell'iperpiano separatore, per cui . Se il punto rispetta il vincolo (2), producendo un certo scalare , allora il prodotto rispetta il vincolo (3):
Analogamente per i punti al di sopra dell'iperpiano.
5.4 Larghezza del margine
L'obiettivo principale è quello di massimizzare il margine, ovvero la distanza tra i vettori di supporto delle due diverse classi. Ma come otteniamo la larghezza del margine? Consideriamo un vettore di supporto di classe ed un vettore di supporto di classe . Ipotizziamo di avere il versore w normale all'iperpiano:

Per ottenere la larghezza del margine, basterebbe proiettare i due vettori di supporto sul versore normale e calcolarne la differenza:
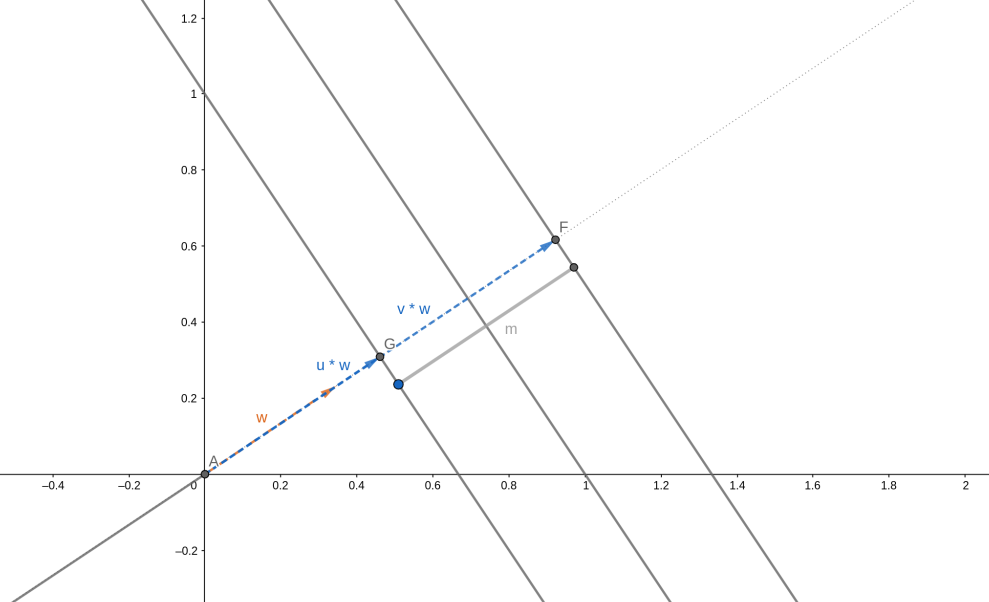
Il vettore dei pesi è ortogonale rispetto all'iperpiano risultante. Per ottenere un versore normale all'iperpiano basta dividere il vettore per la sua norma :
Per cui, definendo con la larghezza del margine, abbiamo che:
Ricordiamo che valgono le condizioni sui vettori di supporto. Iniziamo con che è vettore di supporto per la classe , per cui dalla condizione (1.1) abbiamo che:
Simmetricamente, per il vettore di supporto di classe abbiamo che:
Sostituendo le espressioni 4.1 e 4.2 alla 4, otteniamo che:
5.5 Massimizzare il margine
Trovare l'iperpiano ottimale significa trovare quell'iperpiano che massimizzi la larghezza del margine: Tuttavia, gli studi dimostrano che è matematicamente più conveniente considerare l'analogo problema: Rispetto alla condizione:
5.6 Hard margin e soft margin
Sino ad ora abbiamo considerato il vincolo (3.1) molto restrittivo, per cui all'interno dei margini non vi può risiedere alcun punto. Questo metodo prende il nome di hard margin. Si tratta di una scelta molto rigida, che porta ad un modello estremamente sensibile al rumore. In presenza di rumore, è molto probabile che il modello hard margin produca un iperpiano con una zona di margine molto ristretta, o in generale è frequente ottenere errori da overfitting su dati reali.
Un modello meno sensibile al rumore è il soft margin, il che consiste nell'ammettere che alcuni punti possano trovarsi nella zona di margine, violando i vincoli. Tuttavia, un soft margin troppo permissivo rischia di compromettere l'accuratezza del classificatore. Occorre dunque un trade-off tra la larghezza del margine ed il numero di violazioni del margine consentite al classificatore.
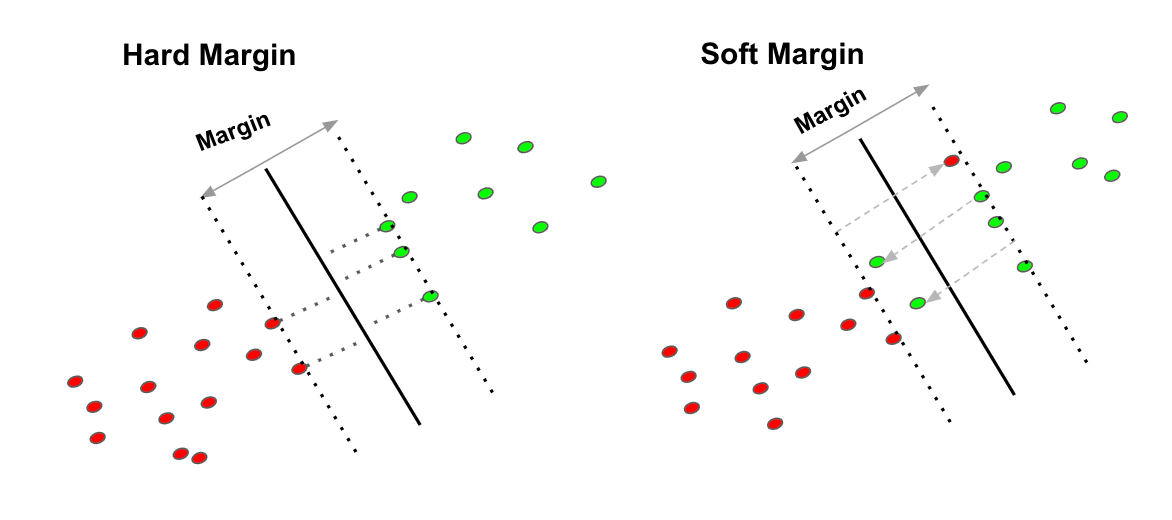
5.7 Classificazione soft margin
Nella classificazione soft margin vengono introdotte n variabili di slack , dove l'i-esima variabile è definita come segue: Ricordiamo che per ogni punto al di fuori dei margini vale il vincolo: Per cui se l'i-esimo punto rispetta il vincolo, allora: Altrimenti, se l'i-esimo punto non è classificato correttamente, ovvero si trova tra e , è proporzionale alla distanza del punto dal margine della classe corrispondente; ovvero più è distante dal margine della classe corretta, più il valore è alto. è il più piccolo numero non negativo che soddisfa la seguente disuguaglianza:
Vogliamo che in media gli siano piccoli. Introduciamo un parametro che costituisce il trade-off tra larghezza del margine e numero di violazioni tollerate. Il problema di ottimizzazione diventa: Soggetto alle condizioni: Più piccolo è il valore , più trascurabile è , ovvero meno importante è la dimensione del margine. Variando possiamo controllare il peso della dimensione del margine nel calcolo dell'iperpiano separatore.
Utilizzando la formulazione di Lagrange, il problema precedente è traducibile nel seguente problema duale: Soggetto alle condizioni: Dove sono i moltiplicatori di Lagrange. Dal momento che la funzione duale è quadratica in , è possibile ricavare tali moltiplicatori utilizzando algoritmi di programmazione quadratica. Una volta ricavati, è possibile calcolare il vettore dei pesi come segue: Mentre la costante di bias può essere calcolata prendendo uno tra i vettori di supporto e risolvendo la seguente equazione rispetto a :
5.8 Mapping di dati non linearmente separabili
Nel caso in cui i dati non siano linearmente separabili, lo spazio di input viene mappato in un nuovo spazio con più dimensioni attraverso una funzione di mapping . Nel nuovo spazio i punti risultano linearmente separabili, quindi è possibile risolvere lo stesso problema di ottimizzazione visto prima, in cui al posto di abbiamo .
Esempio: poniamoci in uno spazio a 3 dimensioni, in cui le osservazioni sono vettori . Supponiamo che in tale spazio, i dati non siano linearmente separabili. Utilizziamo la seguente funzione di mapping: La funzione ricava le ulteriori 3 dimensioni moltiplicando ad ognuna delle componenti la componente . L'equazione dell'iperpiano separatore nello spazio sarà: In generale, il problema di ottimizzazione posto precedentemente è riproponibile utilizzando la funzione che mappa i dati in input: Soggetto alle condizioni:
5.9 Funzioni kernel
Il prodotto può essere più dispendioso da calcolare, dal momento in cui ci troviamo in uno spazio a più elevata dimensionalità. Per ovviare al problema, si utilizzano le funzioni di kernel. Una funzione di kernel K è una funzione che soddisfa la condizione: Essa definisce implicitamente il mapping nel nuovo spazio. Permette di sostituire al prodotto scalare il valore stesso della funzione kernel e di effettuare tutti i calcoli direttamente nello spazio originario che ha meno dimensioni. Vediamo di seguito alcune funzioni kernel tipiche.
Kernel polinomiale di grado H Kernel gaussiano Kernel sigmoide
Durante la costruzione del modello discriminativo è bene provare più funzioni kernel e selezionare quella più adatta, in base ad un indice di performance.
Infine possiamo quindi rappresentare il problema di ottimizzazione mediante funzione di kernel come segue:
Soggetto alle condizioni:
5.10 Conclusioni
Alcune implementazioni di SVM permettono di classificare i dati su più di due classi. L'SVM si presta bene a classificare dati ad elevata dimensionalità ed è meno soggetto ad overfitting rispetto ad altri metodi.
6. Lazy Learning
6.1 Apprendimento eager contro lazy
I modelli classificativi o predittivi possono portare a compimento i propri task con un certo livello di accuratezza imparando dai dati di training. Vi sono due tipi di apprendimento: il primo viene chiamato apprendimento eager (impaziente), il secondo prende il nome di apprendimento lazy (pigro).
- Apprendimento eager (eager learning): dato un training set, si costruisce un modello prima di ricevere nuovi dati da classificare.
- Apprendimento lazy (lazy learning): semplicemente memorizza il training set di dati e calcola la funzione di classificazione nel momento in cui c'è da classificare un nuovo dato.
Tutti i metodi visto fin qui effettuano un apprendimento eager.
I metodi di apprendimento lazy hanno un tempo di predizione più alto, mentre il training è molto veloce, poiché richiede solo la memorizzazione dei dati. La funzione di predizione è approssimata localmente. I metodi lazy sono utili nel caso di grandi dataset con pochi attributi e che si aggiornano continuamente (es. detaset di contenuti multimediali). Per quest'ultimo motivo sono molto utilizzati nei sistemi di raccomandazione (predizione della preferenza che potrebbe esprimere un utente su un item, come un film o un prodotto commerciale). Un esempio di algoritmo che sfrutta l'apprendimento lazy è il kNN.
6.2 kNN - K-Nearest Neighbors
6.2.1 Nearest neighbor algorithm
Supponiamo di avere in input un nuovo dato da classificare. Una buona idea sarebbe quella di assegnare a tale dato la classe dell'osservazione più vicina. È necessario quindi utilizzare una funzione distanza da minimizzare, e molto spesso tale funzione corrisponde alla distanza euclidea: Dove è il numero di feature delle osservazioni. In tal caso la funzione di classificazione non dovrà fare altro che trovare quel dato del training set che minimizzi la funzione distanza :
f(x) = arg \min_\bar x d(x,\bar x)
6.2.2 K-Nearest neighbor algorithm
L'algoritmo precedente non tiene conto dei possibili outliers presenti nel training set, di conseguenza un'idea più accurata è quella di trovare, anziché uno, i primi dati più vicini al dato in input.

6.2.3 Definizione formale dell'algoritmo
Una volta individuata la funzione distanza più appropriata, definiamo: L'intorno di centro e di raggio contenente le osservazioni più vicine ad . indica il training set e è l'iperparametro scelto dall'utente. Determiniamo il raggio tramite tale definizione: Ovvero quel raggio dell'intorno centrato in che comprenda esattamente i più vicini ad . Definiamo infine la funzione di classificazione come segue: Dove per moda si intende la funzione statistica che individua l'elemento più frequente. In questo caso controlla qual è l'etichetta più frequente nei elementi più vicini all'elemento in input.
6.2.4 Scelta di K
Consideriamo le seguenti mappe le quali individuano, al variare di , la classe predominante in una porzione di area. Se è particolarmente piccolo (primo quadrante), allora il piano verrà segmentato in piccole porzioni di area con classi diverse e ciò può provocare overfitting. Tuttavia, un troppo grande andrebbe ad approssimare eccessivamente la scelta, per cui l'algoritmo risulterebbe meno accurato e si avrebbe underfitting. L'iperparametro va calibrato attraverso delle prove su un set di validazione.
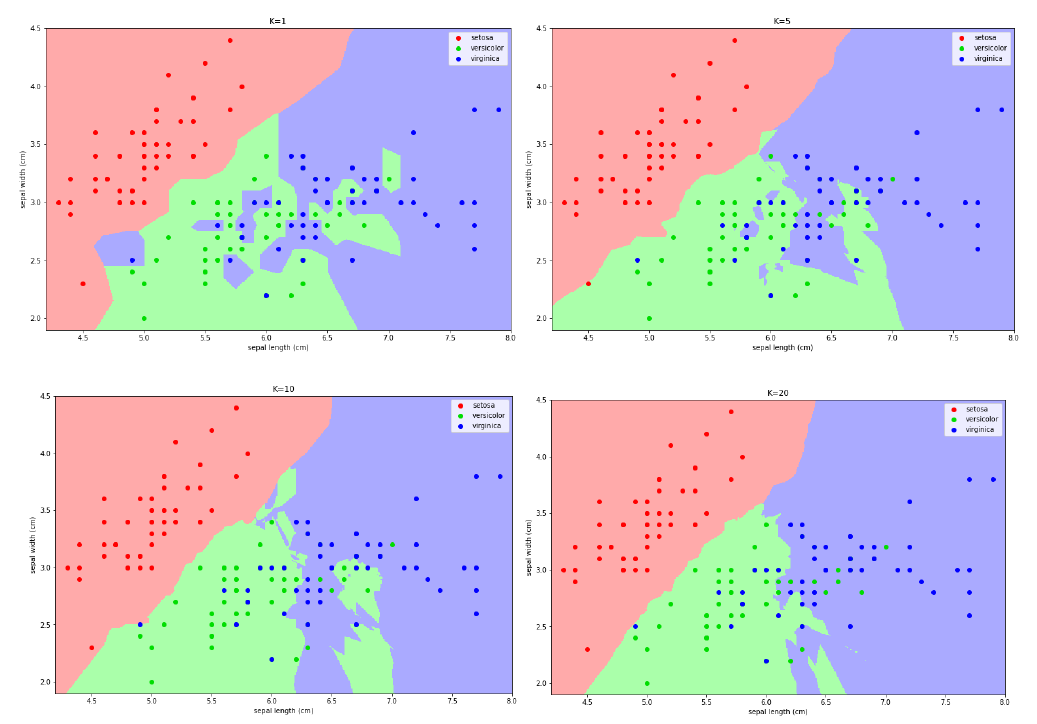
6.2.5 Varianti implementative
Una variante più sofisticata del kNN potrebbe pesare gli oggetti sulla base della distanza:
- Assegna un peso ad ogni oggetto sulla base della distanza dal punto da classificare.
- I punti più vicini hanno un peso maggiore nella classificazione.
- Il peso potrebbe essere calcolato come l'inverso del quadrato della distanza.
6.2.6 Importanza del kNN
Come detto in precedenza, molto spesso è difficile interpretare i risultati degli algoritmi di classificazione (come quelli forniti dalle reti neurali). Nel caso del kNN è possibile utilizzare un k sufficientemente grande e, una volta selezionati i k oggetti più vicini, creare un albero decisionale su tali oggetti che riesca a fornire delle spiegazioni più o meno chiare rispetto all'associazione. Perché allora non costruire un albero decisionale direttamente sui dati di training del kNN? Questo poiché molto spesso si ha a che fare con mole di dati molto ampia, per cui gli alberi decisionali diventano dispendiosi e sconvenienti; al contrario, con kNN si riesce ad estrarre un sottoinsieme di dati localmente connesso al dato da esaminare.
7. Apprendimento ensemble
7.1 Idea principale
L'idea dell'apprendimento ensemble è quella di combinare due o più modelli di apprendimento al fine di ottenere migliori performance di predizione rispetto ai modelli presi singolarmente. In altre parole, vanno combinate ipotesi multiple al fine di ottenere una migliore ipotesi predittiva. Generalmente, con il termine ensemble learning si intende una combinazione di modelli dello stesso tipo (es. alberi decisionali, SVM, etc.). L'ensemble learning richiede molta più computazione, quindi ha senso solo se è usato per combinare algoritmi di apprendimento veloci (come gli alberi decisionali) che non hanno elevata accuratezza se presi singolarmente. Il problema principale è come addestrare i classificatori e come combinarne i risultati.
7.2 Bootstrap o bagging
Una tecnica comune di ensemble learning è il bootstrap o bagging. Siano i modelli da combinare. Dividiamo il training set in sottinsiemi ottenuti mediante campionamento random delle tuple con ripetizioni (bootstrap sampling). Il modelo viene addestrato con il training set . Nel caso della predizione, viene restituita la media dei valori predetti, mentre nel caso della classificazione si restituisce l'etichetta di maggioranza, ovvero quella predetta dal maggior numeri di classificatori.
7.3 Random forest
Il Random Forest è un esempio di modello (classificatore o predittore) ensemble che combina i risultati di diversi alberi decisionali mediante la tecnica bootstrap. In più il Random Forest addestra ciascun albero con un sottoinsieme random di attributi (bagging sugli attributi). Tipicamente se è il numero totale di attributi, per la classificazione, per la predizione. Attributi che risultano essere predittori molto forti vengono prontamente selezionati dagli alberi decisionali. Il bagging sugli attributi diminuisce la correlazione tra i risultati degli alberi.
8. Validazione di un classificatore
8.1 Matrice di confusione
La matrice di confusione è una struttura utile a rappresentare l'accuratezza di un classificatore. Da tale matrice derivano varie metriche che analizzeremo in dettaglio. Sulle righe sono disposti i valori reali, mentre sulle colonne i valori predetti. Vediamo un esempio in figura:
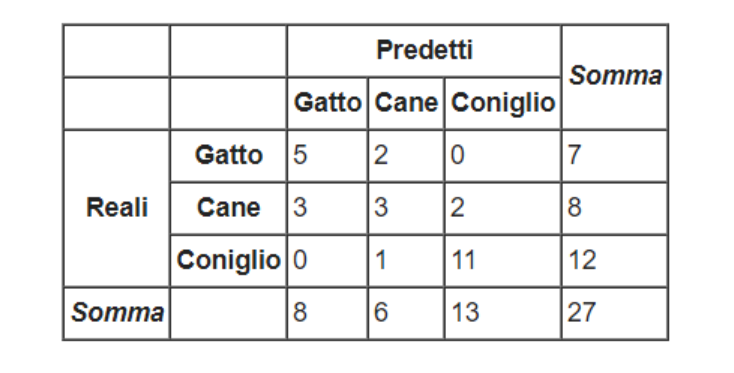
L'elemento contiene il numero di casi in cui il classificatore ha classificato l'osservazione nella classe , quando la classe di appartenenza è . Nel caso in cui allora la classe predetta è corretta: un buon classificatore ha valori alti nella diagonale principale e valori nulli (o molto bassi) nelle altre posizioni.
8.2 Accuratezza & Error rate
Dato un classificatore e la sua matrice di confusione , l'indice di accuratezza misura la percentuale di tuple classificate correttamente da . Nella pratica è molto semplice da calcolare: vengono sommati tutti i valori della diagonale principale e viene rapportata la somma al numero totale di osservazioni classificate. Nell'esempio precedente avremo: Al contrario, possiamo misurare la percentuale di errore, o error-rate, del classificatore sommando tutti gli elementi che non risiedono nella diagonale principale e rapportandoli al numero totale di osservazioni classificate. Tuttavia, l'error-rate è complementare all'accuratezza, per cui è possibile calcolare solo la prima e derivare l'errore come segue:
8.3 Accuratezza per classificatori binari
Supponiamo di avere un dataset con due sole classi, una indicata come (positiva) ed una indicata come (negativa). Indichiamo con e l'insieme delle osservazioni di classe ed rispettivamente. Sulla base dell'esito della classificazione possiamo distinguere 4 sottoinsiemi di tuple:
| Nome | Descrizione | Simbolo |
|---|---|---|
| True positive | tuple di classe P classificate come P | |
| True negative | tuple di classe N classificate come N | |
| False positive | tuple di classe N classificate come P | |
| False negative | tuple di classe P classificate come N |
Vedremo adesso una lista di metriche possibili solo nel caso di un classificatore binario, che evidenziano particolari aspetti del classificatore.
8.3.1 Metriche per classificatori binari
La recall, anche chiamata sensitività o più tecnicamente true positive rate, è la percentuale di osservazioni positive classificate correttamente: La specificità, o più tecnicamente True Negative Rate, è la percentuale di osservazioni negative classificate correttamente: La false positive rate è la percentuale di osservazioni negative classificate come positive. Ipotizziamo che il modello classifichi pazienti tra positivi ad un tipo di tumore o negativi: si vuole una FPR tendenzialmente bassa per evitare che al paziente siano provvisti risultati sgradevoli. Il false discovery rate è una metrica che indica la percentuale di falsi positivi rispetto a tutte le osservazioni classificate come positive (corrette o meno che siano): La precision è la percentuale di osservazioni classificate correttamente come positive rispetto alle osservazioni classificate positive (corrette o meno che siano):
Qual è la differenza tra precision e recall? Ipotizziamo di avere un dataset di 50 osservazioni, 25 di classe P e 25 di classe N. Ipotizziamo che il classificatore classifichi solo 5 osservazioni come positive, e che tali classificazioni siano corrette. Il modello non è stato in grado di rilevare la maggior parte delle osservazioni positive, di fatto avremo una recall del 20% (). Tuttavia, le osservazioni classificate come positive sono tutte corrette, per cui la precision è del 100% ().
Sia la precision che la recall sono importanti quando si giudica un classificatore, è però possibile valutare entrambi attraverso una sola metrica, chiamata score F1. Lo score F1 è compreso tra 0 ed 1 e consiste in una media armonica tra le due metriche: Se sia la precision che la recall hanno un valore alto, allo lo score F1 sarà anch'esso alto. Questa è una proprietà della media armonica, per cui si preferisce rispetto alla media canonica. Vediamo la differenza tra le due:
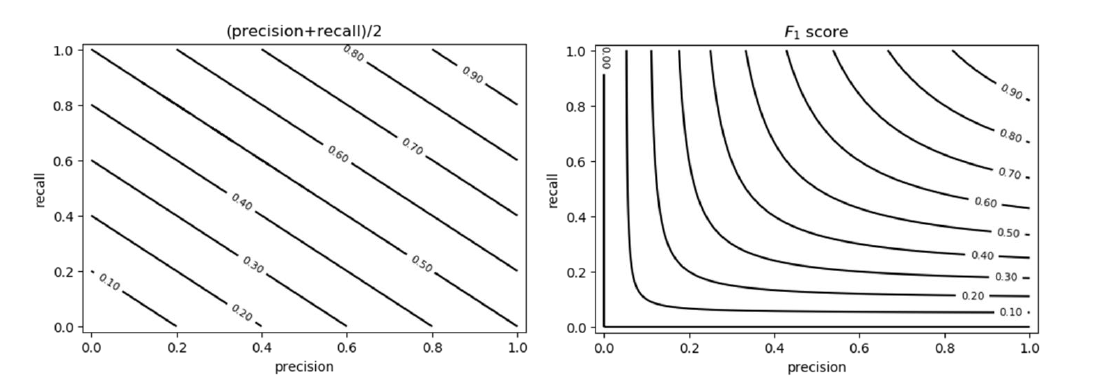
8.3.2 Soglia discriminativa nei classificatori binari
Se il classificatore in analisi utilizza un valore soglia per effettuare la classificazione, allora le misure di performance vanno rivalutate al variare della soglia discriminativa.
8.4 Receiver Operating Characteristic Curve (ROC)
La curva ROC rappresenta il True Positive Rate (TPR), detto anche numero di hits, in funzione del False Positive Rate (FPR), detto anche numero di falsi allarmi, al variare della soglia . Vediamo due casi limite:
a) Nel caso limite in cui la soglia sia così alta che tutte le tuple sono classificate come negative, allora significa che nessuna tupla sarà classificata come positiva. Per cui entrambe le metriche TPR e FPR saranno nulle.
b) Nel caso limite in cui la soglia sia cosi bassa che tutte le tuple sono classificate come positive, allora significa che tutte le tuple negative sono classificate come positive, per cui il False Positive rate è massimo (FPR = 1), ed anche tutte le tuple positive sono classificate come positive (TPR = 1).
Al diminuire della soglia, aumenta il numero di tuple classificate come positive e contestualmente entrambi gli indici aumentano (in misura diversa). La situazione ideale è quella in cui TPR aumenta fino a raggiungere il valore 1 ed FPR si mantiene pari a 0, per cui si ha il miglior classificatore. La curva roc diventa banalmente una funzione scala. Un classificatore random avrà sempre uguali valori di TPR ed FPR al variare di .
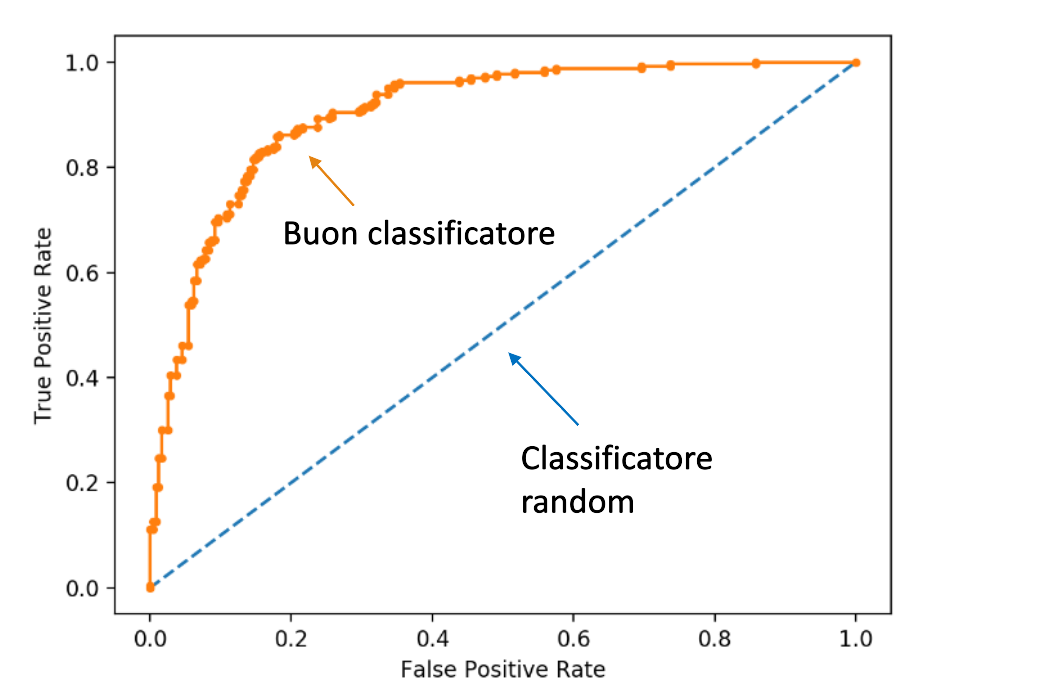
8.5 Precision-Recall curve (PR)
La curva ROC è ottima nel caso di dataset bilanciati, mentre in presenza di dataset sbilanciati è più conveniente analizzare la curva PR, che rappresenta la precision in funzione della recall al variare della soglia discriminativa .
a) Nel caso limite in cui la soglia sia così alta che tutte le tuple sono classificate come negative, allora significa che nessuna tupla sarà classificata come positiva. La recall sarà nulla poiché nessuna osservazione positiva sarà rilevata, mentre la precision sarà massima poiché tutte le osservazioni positive rilevate (0) sono correttamente classificate.
b) Nel caso limite in cui la soglia sia cosi bassa che tutte le tuple sono classificate come positive, allora significa che tutte le tuple positive verranno rilevate, per cui la recall = 1. Tutta via la precision sarà bassa poiché il numero di osservazioni positive classificate correttamente sarà diviso per la cardinalità del dataset.
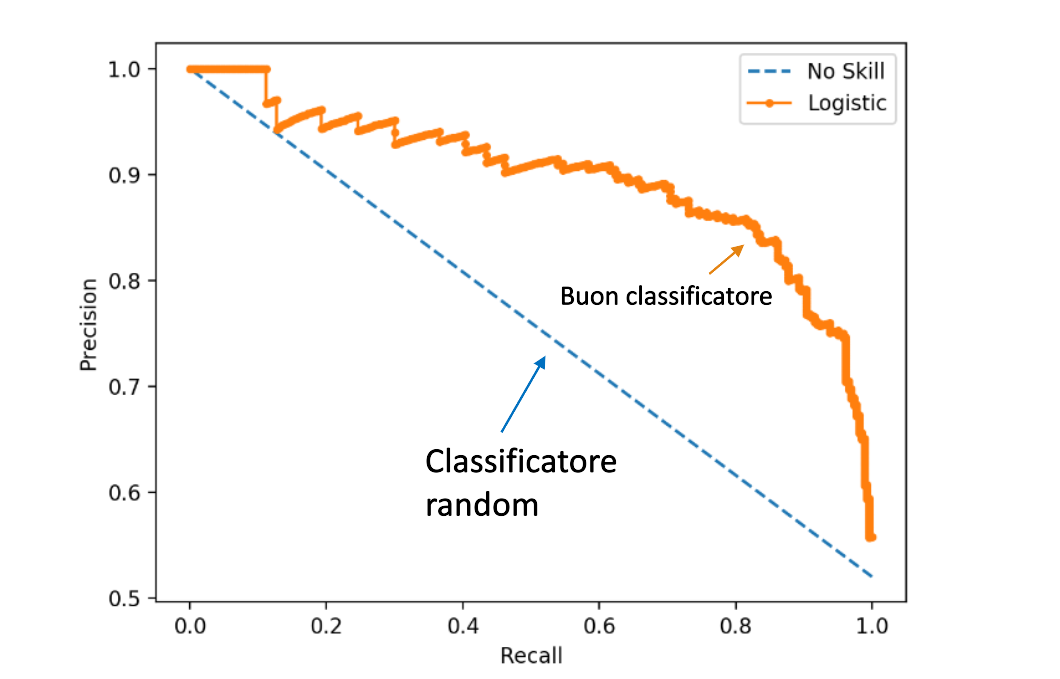
8.6 Area under the curve (AUC)
Come indicatore di accuratezza del classificatore si fa riferimento all'area sottesa alla curva, chiamata AUC (area under the curve). Tale metrica vale sia per le curve ROC che per le PR. Essa assume valori tra 0 ed 1, dove 1 denota un classificatore perfetto.
8.7 Validazione di un classificatore
Per validare un classificatore viene partizionato il dataset in training set, test set ed eventualmente un validation set su cui testare gli iperparametri. Vi sono vari metodi per effettuare il partizionamento, tra cui il metodo holdout ed il k-fold cross-validation.
8.7.1 Metodo holdout
Fissata una percentuale , il dataset viene partizionato in due set indipendenti, il training set con l'% del dataset e il test set con il % del dataset. Si addestra il modello sul training set, si classifica il test set e si misurano le performance sui risultati ottenuti. Esiste una variante chiamata random sampling, in cui l'holdout viene ripetuto volte (con le stesse proporzioni), e si calcola la media delle accuratezze ottenute ad ogni esecuzione.
8.7.2 K-fold cross-validation
Fissato , si partiziona il dataset in partizioni approssimativamente della stessa dimensione. Alla i-esima iterazione () si considera la partizione come test set ed il resto come training set. Una estremizzazione del metodo è il leave one out, dove è il numero di tuple ed il test set è di volta in volta una sola tupla.
Predizione
1. Introduzione
La predizione è simile alla classificazione poiché costruisce un modello e usa il modello per predire valori per un dato input. La predizione è diversa rispetto alla classificazione poiché la classificazione predice valori categoriali (etichette), mentre la predizione modella funzioni a valori continui.
Diversi classificatori possono essere utilizzati come predittori (alberi decisionali, SVM), e viceversa (regressione logistica). La tecnica più importante di predizione è la regressione.
2. Regressione
La regressione è una forma di apprendimento supervisionato che consente di apprendere una mappatura tra i dati di input e i corrispondenti output. Esempi di task legati alla regressione sono:
- Predizione del prezzo di prodotti date delle caratteristiche
- Predizione del profitto di una certa compagnia
- Contare il numero di automobili presenti in una immagine.
2.2 Definizione formale
Definiremo un regressore come una funzione dove è la dimensionalità del dominio (features dei dati in input) ed è la dimensionalità del codominio (features dei dati in output). In generale, ci riferiremo ad un dato in input con , all'output vero legato ad con e all'output predetto dal regressore con . Possiamo predire un valore a partire da : In questo contesto, spesso è chiamata variabile indipendente, mentre è chiamata variabile dipendente. Come visto nella classificazione, possiamo definire una funzione di rappresentazione per mappare un input da ad . Utilizzando la funzione di rappresentazione, possiamo predire il valore per un input : Per trovare la funzione di regressione possiamo utilizzare vari metodi a seconda del contesto. Vedremo la regressione lineare, la regressione lineare multipla, la regressione polinomiale e quella logistica.
2.3 Misure di performance
Sia il test set su cui validare il regressore. Definiamo: l'insieme degli output corretti (o etichette di ground truth), e: l'insieme di output predetti. Idealmente vorremmo che gli output predetti siano quanto più vicini agli output corretti (nel caso migliore ). Dal momento in cui gli elementi di entrambi gli insiemi sono vettori di egual dimensione, definiremo le misure di performance come misurazioni di vicinanza o verosimiglianza tra gli output predetti e gli output corretti.
2.3.1 Mean Squared Error (MSE)
Consideriamo per ogni elemento del test set la corrispondente etichetta di ground truth e l'etichetta predetta dalla funzione di regressione . Le etichette hanno dimensione , quindi una buona misura di vicinanza tra le due è spesso la distanza euclidea: Per risparmiare il tempo computazionale impiegato nel calcolo della radice quadrata, spesso si utilizza la distanza euclidea quadratica: A questo punto, l'MSE consiste nel calcolare l'errore medio per tutti gli input del test set:
2.3.2 Root Mean Squared Error (RMSE)
L'unità di misura dell'MSE è il quadrato dell'unità di misura della variabile dipendente (). Nella pratica, se è misurata in metri, l'errore MSE sarà misurato in metri quadrati . Per ovviare a questo possiamo utilizzare il root mean squared error (RMSE):
2.3.3 Mean absolute error (MAE)
Se le etichette sono scalari (), allora possiamo misurare l'errore e mantenere la stessa unità di misura attraverso il mean absolute error, ovvero la media delle differenze tra le etichette in valore assoluto:
2.3.4 Differenza tra MSE, RMSE e MAE
Tutte e tre le misure di performance sono misure di errore, per cui un buon regressore dovrebbe puntare a minimizzarle. La principale differenza tra gli indici presentati sta nel fatto che MSE e RMSE enfatizzano l'errore al crescere della distanza tra i punti, mentre tralasciano gli errori piccoli. Tuttavia, MAE risulta più intuitivo.
2.4 Casi speciali di regressione
Mentre la regressione può essere definita in maniera generale con una funzione: Vi sono alcuni casi molto frequenti in cui vi sono particolari valori di ed , noi vedremo i seguenti.
Regressione semplice La regressione semplice prevede che , per cui il task consiste nel mappare numeri scalari a numeri scalari con una funzione :
Regressione multipla La regressione multipla si ha quando ed , e consiste nel mappare vettori su scalari con una funzione :
Regressione multivariata La regressione multivariata è quella più generale, dove ed è arbitrario. Consiste nel mappare vettori o scalari (nel caso ) su vettori con una funzione :
3. Regressione lineare
Vedremo il metodo della regressione lineare applicata su casi di regressione semplice, multipla e multivariata.
3.1 Regressione lineare semplice
La regressione lineare semplice consiste nel trovare una funzione di forma . Per iniziare, consideriamo un esempio in cui il dataset consiste in coppie referenti:
- Il numero medio di stanze in una casa in un quartiere;
- Il prezzo medio delle case nel quartiere (misurato in , es. = )
Disegniamo un plot del dataset ponendo il numero medio di stanze sull'asse delle ed il prezzo medio sull'asse delle :
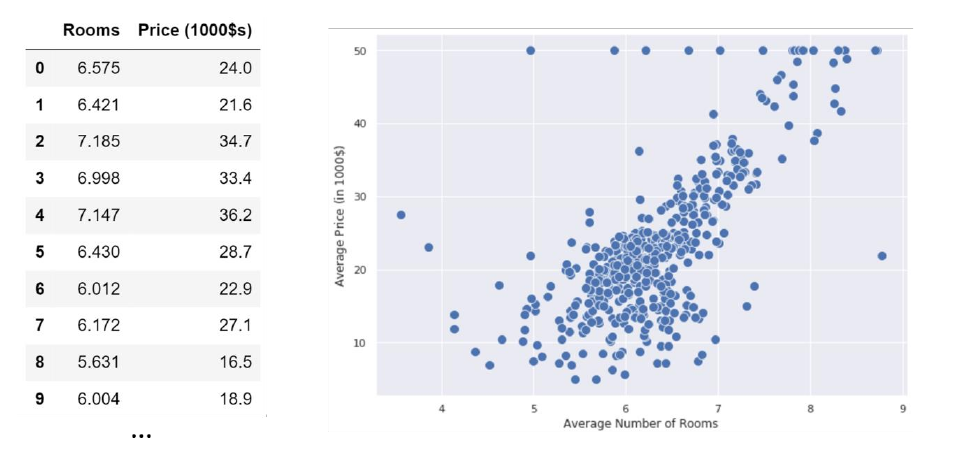
Vorremmo idealmente trovare una funzione che riesca ad approssimare il prezzo medio delle case dato un numero di stanze medio . Dal plot osserviamo che il prezzo aumenta proporzionalmente al numero di stanze. Calcolando la covarianza otteniamo , il che è un'altra conferma della correlazione tra le due variabili. Esse seguono circa un andamento lineare, quindi sono approssimativamente distribuite lungo una retta:
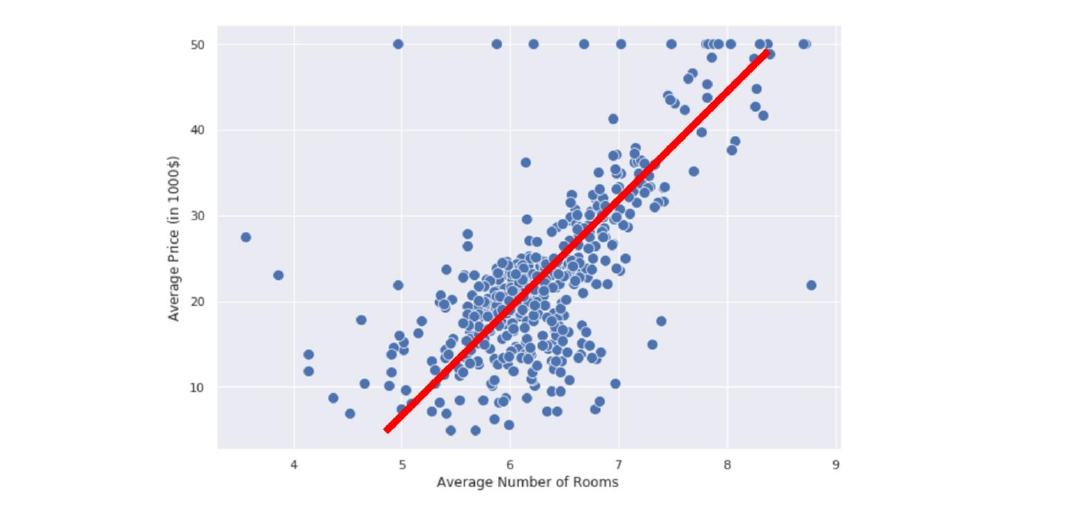
Possiamo quindi costruire la nostra funzione di regressione utilizzando la formulazione analitica di una retta: Dove è il coefficiente angolare e è l'intercetta. Anziché e utilizzeremo rispettivamente e . Tale notazione ci aiuterà a generalizzare la regressione al caso multiplo. Chiamiamo la funzione modello lineare o regressore lineare, dove e sono i parametri del modello. Allenare un modello lineare significa trovare quei valori nei parametri e tale che dia una buona predizione di . Vedremo due metodi per fare ciò: il metodo dei minimi quadrati e la discesa del gradiente.
Consideriamo il precedente esempio e immaginiamo che qualcuno abbia allenato il modello lineare e che i parametri siano e , per cui il nostro regressore lineare sarà così definito: Se proviamo a plottare la linea in figura, essa sarà quella retta con maggiore densità lineare e avrà, nel caso migliore, una misura di errore bassa.
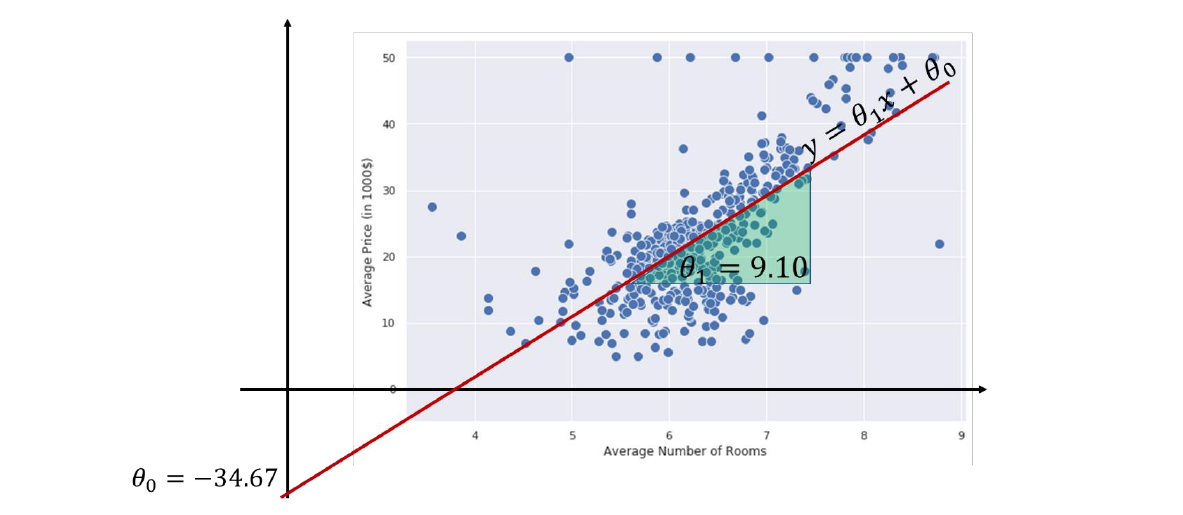
3.2 Interpretazione geometrica
Sappiamo che i valori hanno un ben preciso significato geometrico:
- è l'intercetta: esprime la posizione di nello spazio, ovvero dove intercetta la retta quando .
- è il coefficiente angolare: esprime l'orientamento di rispetto all'asse .
In generale, i due coefficienti hanno specifici effetti geometrici. Rispetto al coefficiente angolare:
- Un valore alto di da luogo a curve più ripide;
- corrisponde ad una retta orizzontale, quindi parallela all'asse delle ;
- rappresentano rette "all'indietro";
Rispetto all'intercetta:
- Il valore decide dove sta la retta nello spazio;
- Valori alti di spingono sopra la retta, per cui si hanno valori alti di (e viceversa)
3.3 Interpretazione statistica
Dall'interpretazione geometrica possiamo tirar fuori alcune considerazioni statistiche:
-
L'intercetta è il valore che si ottiene quando l'input è nullo: .
-
Il coefficiente angolare indica la ripidità della retta: rette più ripide indicano che piccole variazioni su riflettono grandi variazioni su , di fatti possiamo osservare la dipendenza diretta da: Ciò implica che quando osserviamo un incremento di 1 unità su , si riflette un incremento di unità su y.
3.4 Correlazione contro causa
Dovremmo sempre attenzionare l'interpretazione dei coefficienti di un regressore lineare. Un regressore cattura la correlazione tra le variabili indipendenti, ma non ne spiega il perché. Ciò implica che, se l'incremento di una unità su una variabile indipendente si riflette in un aumento di un numero di unità nella variabile dipendente, non dovremmo stabilire nessun tipo di correlazione formale, poiché stiamo solo osservando l'avvenimento di due fenomeni in contemporanea.
3.5 Regressione lineare multipla
Possiamo facilmente estendere la regressione lineare semplice al caso della regressione lineare multipla. Cerchiamo adesso una funzione definita come . In tal caso dovremmo trovare un parametro per ognuna delle dimensioni della variabile in input, più un parametro per l'intercetta: I parametri sono quindi . Allenare il regressore significa trovare un insieme di parametri appropriato per prevedere i valori con migliore accuratezza raggiungibile. La funzione sarà quindi in generale un iperpiano ad dimensioni.
Per convenzione e semplicità di espressione, poniamo e scriviamo il modello lineare come segue: Cosicché l'intercetta sia moltiplicata ad 1, e quindi non vari.
Consideriamo un esempio in cui , nel quale si vuole predire il prezzo di una casa in un quartiere a partire dal numero medio di stanze e dal tasso di criminalità nel quartiere.
Essendo la somma delle dimensioni uguale a 3, possiamo visualizzare un plot tridimensionale dei nostri punti:
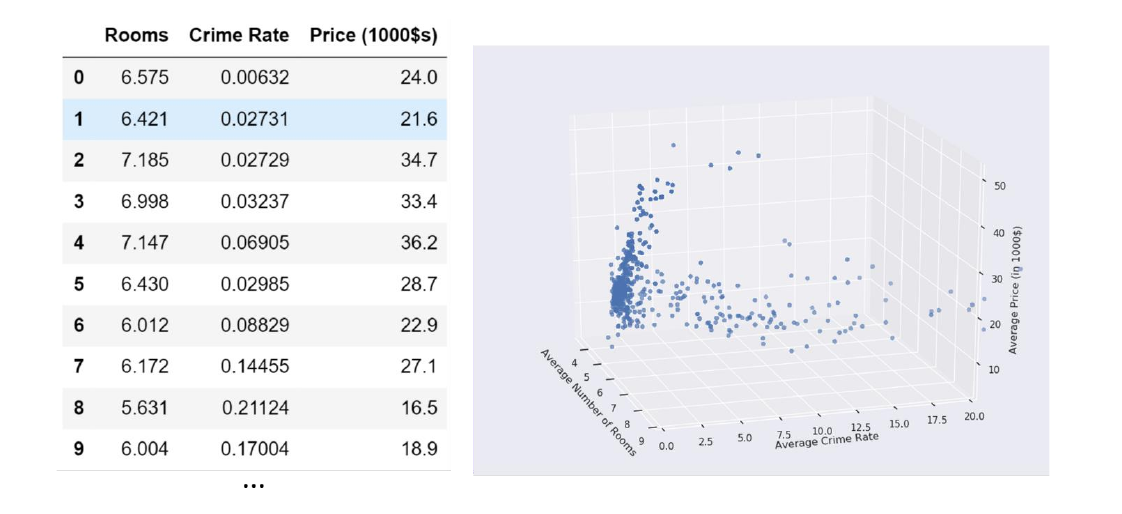
In tal caso il modello lineare sarà: Assumiamo che il modello sia già stato allenato e che i parametri siano i seguenti: Tali parametri identificano il piano nello spazio che meglio approssima la relazione tra i valori in input ed il prezzo da predire:
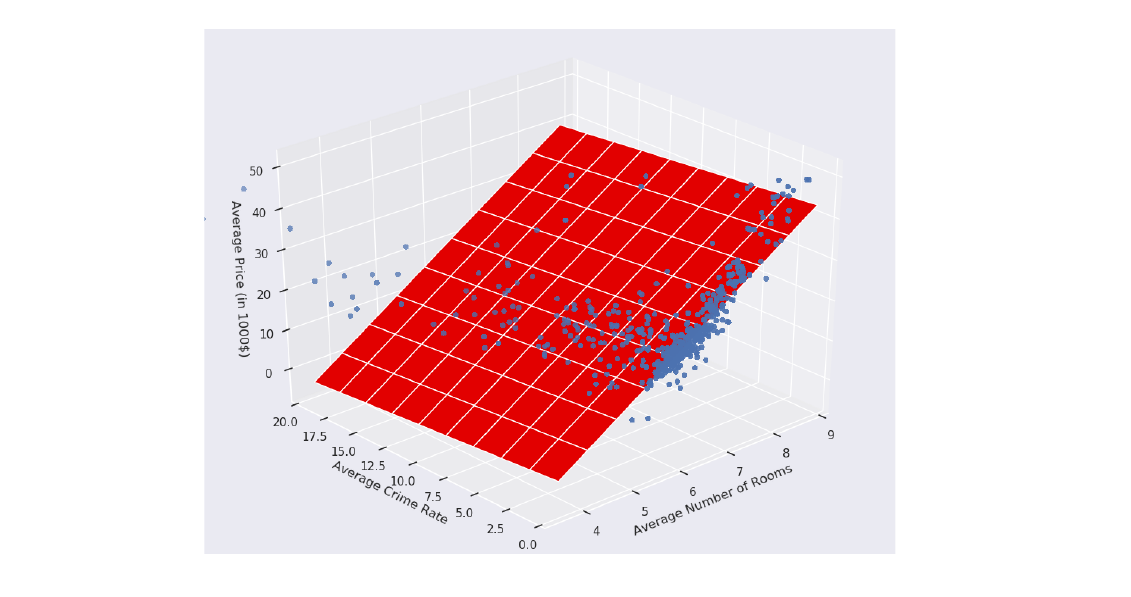
Allo stesso modo possiamo tirar fuori dei significati geometrici e statistici dai coefficienti:
- è il valore di quando tutte le (per non nulla);
- Osserviamo un incremento di unità quando l'i-esima dimensione aumenta di una unità e le altre restano costanti.
3.6 Regressione lineare multivariata
Consideriamo l'ultimo caso, ovvero quello della regressione lineare multivariata. Si cerca una funzione definita come . Il metodo della regressione lineare multivariata risolve il problema definendo regressori multipli indipendenti, uno per ogni dimensione dell'etichetta in output, che processano gli stessi input con pesi differenti: Ognuno dei regressori ha il proprio insieme di parametri , calcolati ed ottimizzati in maniera indipendente dagli altri regressori.
4. Il problema dell'apprendimento
Per capire come tirar fuori i parametri dal regressore ci concentreremo sul caso della regressione multipla, più generico rispetto alla regressione lineare e che pone le fondamenta per quella multivariata. Avremo quindi un regressore : Dove indica il fatto che il regressore dipenda dai parametri . Allenare il regressore significa lasciare che il regressore apprenda quali siano i parametri che minimizzino l'errore di predizione nel training set . Possiamo quantificare l'errore attraverso una funzione costo: Osserviamo che l'espressione sopra è l'indice MSE calcolato sul training set per una certa configurazione di parametri , a meno di una differenza nel prima fattore, che risulta essere anziché . Questa scelta risulterà conveniente in futuro nel metodo della discesa del gradiente. Vorremmo idealmente che la funzione costo sia prossima zero. Di conseguenza, una buona scelta di è quella che minimizza la funzione :
4.1 Metodo dei minimi quadrati
Prima di passare al metodo della discesa del gradiente, vediamo un metodo leggermente più statistico e diretto, il metodo dei minimi quadrati (least squares method). Supponiamo di trovarci nel caso della regressione semplice, per cui:
Il metodo fornisce delle formule dirette per trovare i coefficienti della retta che meglio approssima l'andamento dei punti:
Dove e sono i valori medi. È possibile estendere il metodo dei quadrati minimi per la regressione polinomiale, ma non affronteremo questa tematica.
4.2 Algoritmo di discesa del gradiente
Abbiamo letto nel problema dell'apprendimento che l'insieme di parametri assunti dal modello deve minimizzare la funzione costo . Un approccio naïve potrebbe suggerire di provare tutte le possibili combinazioni di , ma essendo un numero massivo risulta subito un cattivo approccio.
Per risolvere tale problema si possono utilizzare molte strategie di ottimizzazione: quella che utilizzeremo prende il nome di algoritmo di discesa del gradiente, il quale permette di minimizzare qualsiasi funzione differenziabile rispetto ai propri parametri.
4.2.1 Esempio ad una variabile
Supponiamo di avere una funzione convessa come in figura, ovvero una funzione con un solo minimo locale.
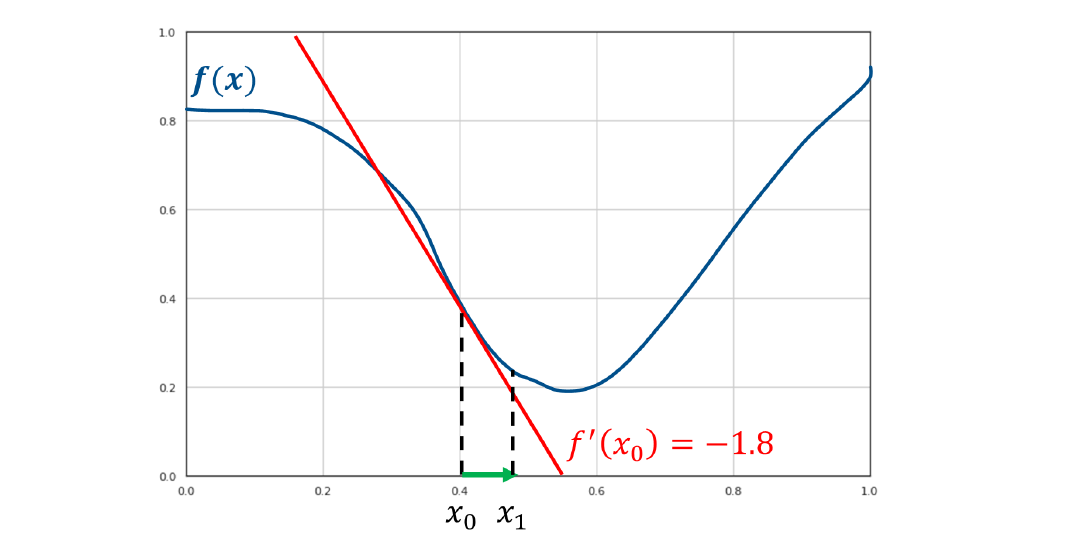
Supponiamo di partire da un punto qualsiasi, per trovare il minimo bisogna seguire l'andamento decrescente della funzione. Tuttavia non abbiamo abbastanza informazioni per sapere come muoverci, quindi è necessario utilizzare uno strumento matematico che dia informazioni sull'andamento della funzione: la derivata.
La derivata fornisce la pendenza (coefficiente angolare) della retta tangente al punto in cui viene calcolata. Di fatto, la retta tangente ci comunica in che direzione la funzione aumenta o diminuisce nell'intorno del punto.
Se il coefficiente angolare è positivo, allora la retta è crescente nel verso dell'asse delle , e quindi lo è anche la funzione, per cui allo scopo di trovare il minimo è necessario muoversi verso sinistra. Viceversa nel caso in cui si ottienga un coefficiente angolare negativo.
Nella funzione d'esempio la derivata ha coefficiente angolare negativo, per cui la funzione è decrescente nel punto e conviene prendere il prossimo punto verso destra, di fatto ma .
La direzione corretta per trovare il minimo è la direzione inversa alla tangente ottenuta attraverso la derivata.
L'algoritmo di discesa del gradiente è un algoritmo iterativo che si sposta nella direzione decrescente della funzione sino a trovare il minimo, ovvero quando la derivata risulta nulla. Ma di quanto ci muoviamo lungo l'asse delle ad ogni step?
Ad ogni step ci muoveremo sull'asse delle proporzionalmente al valore della derivata. Tale euristica è basata sull'osservazione che valori maggiori, in valore assoluto, della derivata indicano pendenze più ripide, quindi si è probabilmente più lontani dal minimo. Scegliendo una costante chiamata learning rate, ci muoveremo ad ogni step nel seguente modo: Osserviamo che, come sperato, se la derivata è negativa, ci muoveremo verso destra di un fattore , viceversa per la derivata positiva. Vediamo come procede l'algoritmo nel nostro esempio di prova:
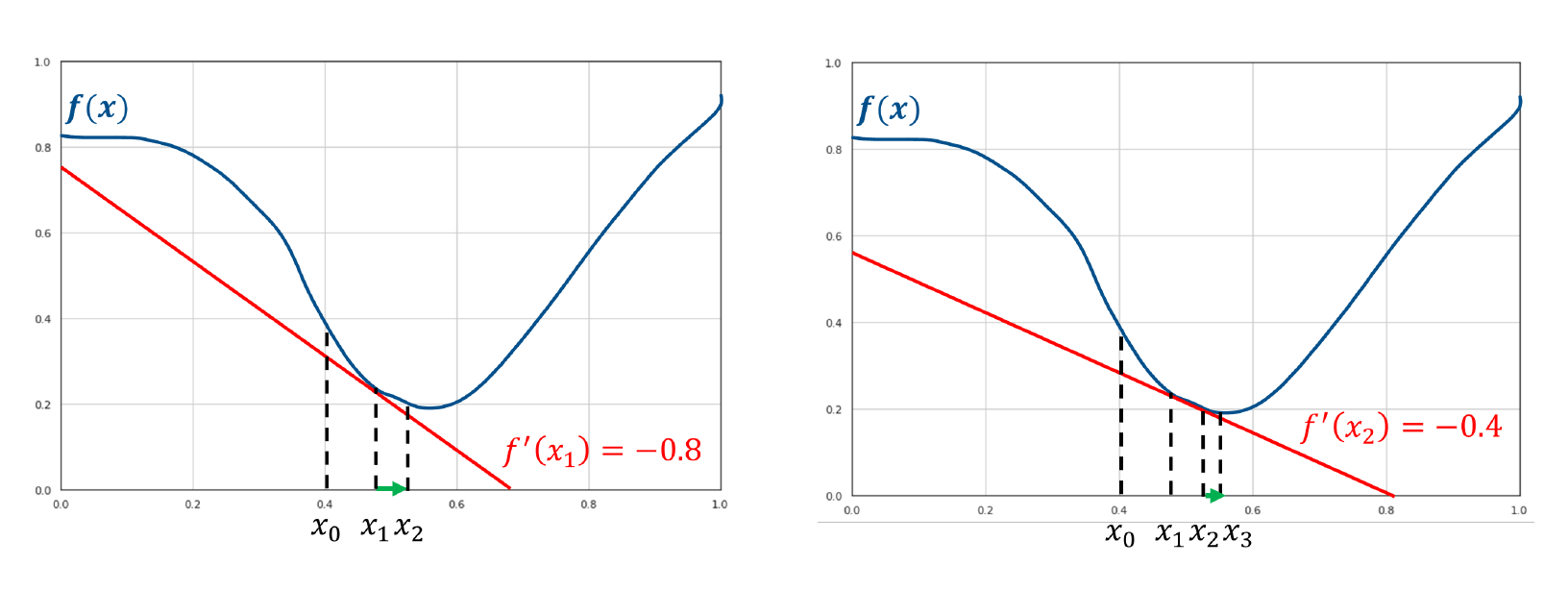
Nel punto la derivata è così vicina allo 0 che approssima quasi perfettamente il minimo. Per cui soddisfa l'espressione: Nella pratica, l'algoritmo finisce la sua iterazione in due casi:
- Un numero massimo di iterazioni è stato raggiunto;
- Il valore è al di sotto di una data soglia.
Nel caso di una variabile, possiamo riassumere l'algoritmo attraverso il seguente pseudocodice:
def gradient_descend():
g = get_learning_rate()
max_loops = get_max_loops()
t_threshold = get_termination_threshold()
x = random()
loops = 0
while (x > t_threshold && loops < max_loops):
m = f'(x)
x = x - (g * m)
return x
4.2.2 Caso multivariato
L'algoritmo di discesa del gradiente è generalizzato nel caso in cui la funzione da ottimizzare sia a più variabili . Per funzioni a più variabili, anziché la derivata è necessario considerare il gradiente, da cui il nome dell'algoritmo.
Il gradiente è una generalizzazione della derivata per funzioni a più variabili.
Il gradiente di una funzione ad variabili in un punto è un vettore la cui -esima componente è data dalla derivata parziale della funzione rispetto alla -esima variabile calcolata nel punto : Nel caso in cui la funzione sia a due variabili, si potrebbe costruire un plot tridimensionale come segue. In tal caso, il gradiente sarà un vettore a due dimensioni e varierà punto per punto.
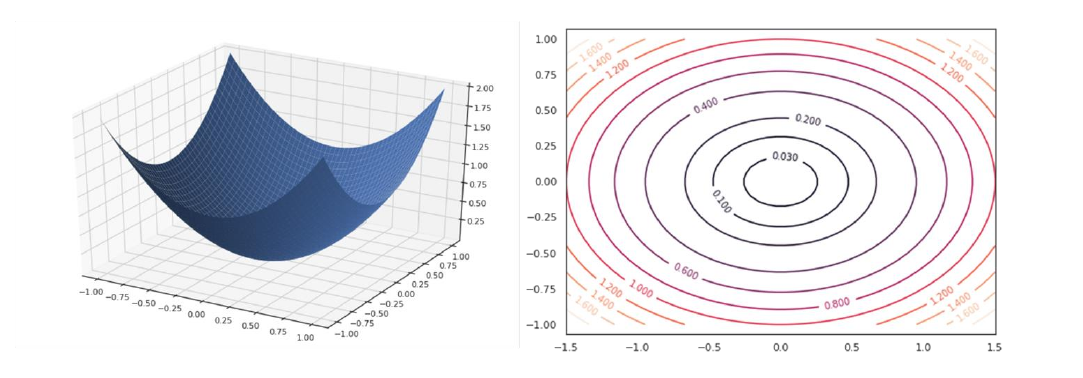
La figura che segue mostrerà graficamente l'andamento che deve seguire la procedura nel caso multivariato:
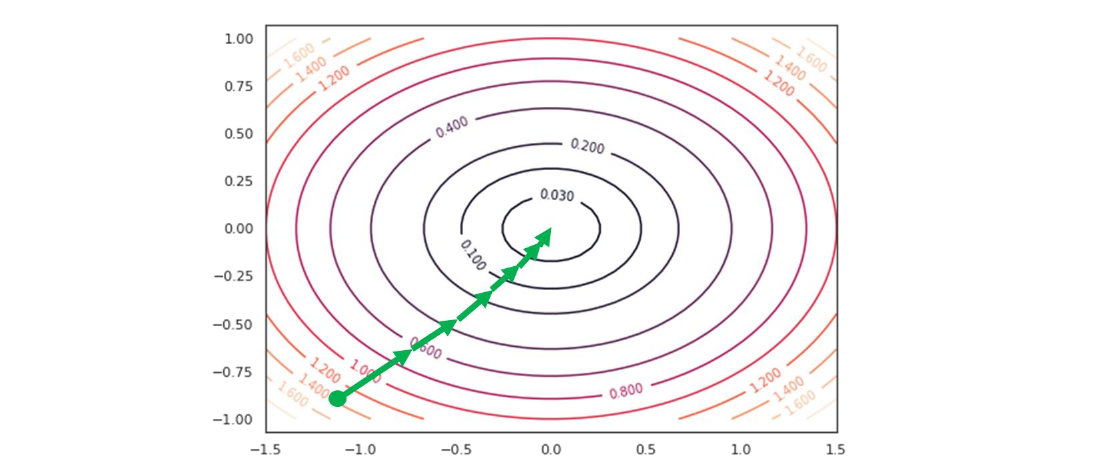
Il ragionamento è analogo, ma l'aggiornamento dei pesi va fatto per ogni variabile. Di conseguenza i passi che seguirà l'algoritmo sono i seguenti:
-
Inizializzare in maniera randomica
-
Per ogni variabile :
- Calcolare la derivata parziale nel punto :
- Aggiornare utilizzando la formula precedente:
-
Ripetere i primi due passi sino a soddisfarre un criterio di terminazione.
4.3 Discesa del gradiente e regressione lineare
Utilizzeremo l'algoritmo di discesa del gradiente per risolvere il problema di ottimizzazione della regressione lineare, quindi per trovare i coefficienti ottimali : Il primo passo è quindi inizializzare randomicamente e applicare iterativamente la regola di aggiornamento per ogni variabile: È necessario quindi calcolare la derivata parziale rispetto a ciascuno dei parametri in input. Scriviamo prima la funzione costo nei termini dei parametri : Esplicitandolo: Dove ricordiamo che per convenzione.
Possiamo calcolare facilmente la derivata parziale di questa funzione rispetto alla -esima componente : Ma notiamo che: Quindi sostituendo e semplificando otteniamo che: La regola di aggiornamento può essere scritta come segue: Con la regola di aggiornamento abbiamo tutto ciò che ci serve per implementare l'algoritmo computazionalmente, utilizzando criteri di terminazione basati sul numero di iterazioni o sulla soglia di aggiornamento.
4.4 Considerazioni sul learning rate
Il learning rate è un iperparametro da determinare. Possiamo utilizzare un validation set per effettuare delle prove e selezionare il valore con risultati migliori. Alcune considerazioni sul learning rate sono:
- Un learning rate basso converge più lentamente ma con buona precisione.
- Un learning rate alto converge più velocemente ma con una precisione peggiore. Può inoltre capitare una situazione di stallo in cui si salta continuamente da un punto a tangente crescente ad un punto a tangente decrescente, generando un effetto ping pong.
5. Regressione non lineare
La regressione lineare risulta limitante nei casi in cui la relazione tra le variabili indipendenti e la variabile dipendente è chiaramente non lineare. Consideriamo ad esempio il seguente plot:
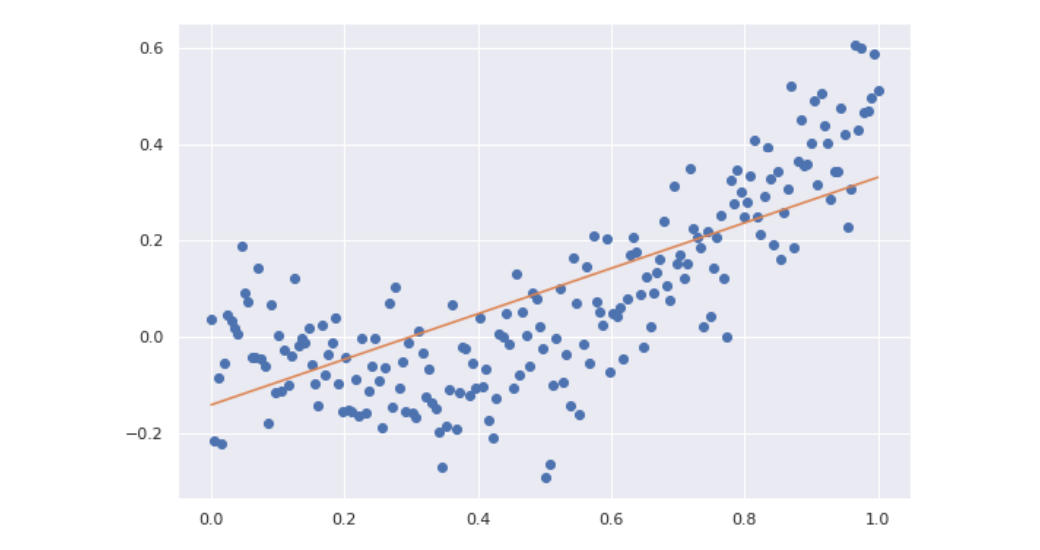
La relazione tra le variabili segue chiaramente una curva anziché una retta. Utilizzare la regressione lineare produrrebbe sicuramente fenomeni di underfitting.
5.1 Regressione polinomiale
Anziché utilizzare una funzione lineare , potremmo introdurre parametri addizionali e utilizzare una funzione polinomiale come segue: Dove rappresenta la potenza -esima di e non l'indice rispetto al training set. Modelli polinomiali di grado più alto consentono di rappresentare funzioni non lineari:
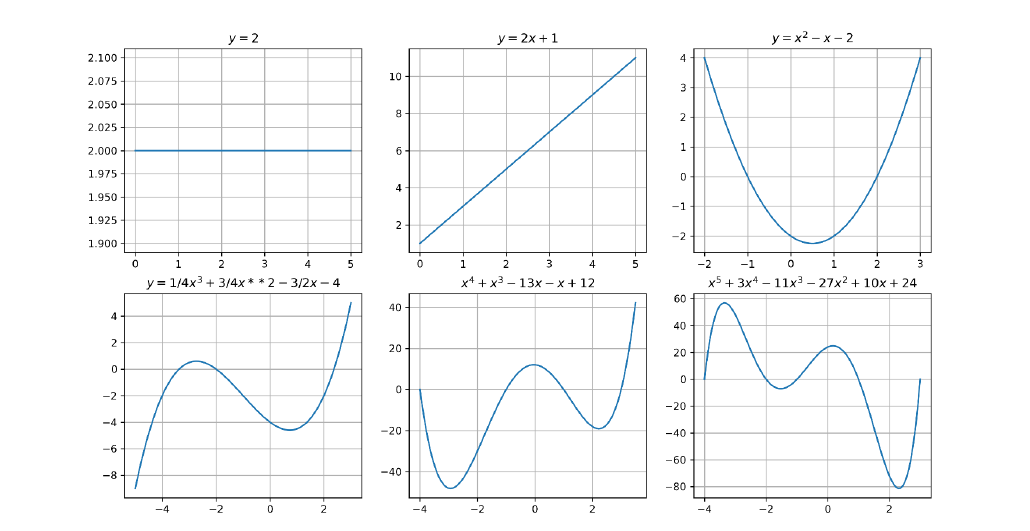
Più alto è il grado del polinomio, più si possono ottenere curve complesse. Possiamo facilmente osservare che anche se la funzione non è lineare rispetto ad , essa è lineare rispetto alle variabili . Determinate le variabili , trovare i coefficienti è comunque un problema di regressione lineare, risolvibile attraverso l'algoritmo di discesa del gradiente.
Osserviamo che possiamo trasformare un problema di regressione lineare in uno polinomiale replicando volte lo scalare e prendendo progressivamente le potenze sino al grado . Se allora: Se applichiamo questo metodo all'esempio precedente con un grado avremo un risultato di gran lunga più adatto rispetto ad una retta;
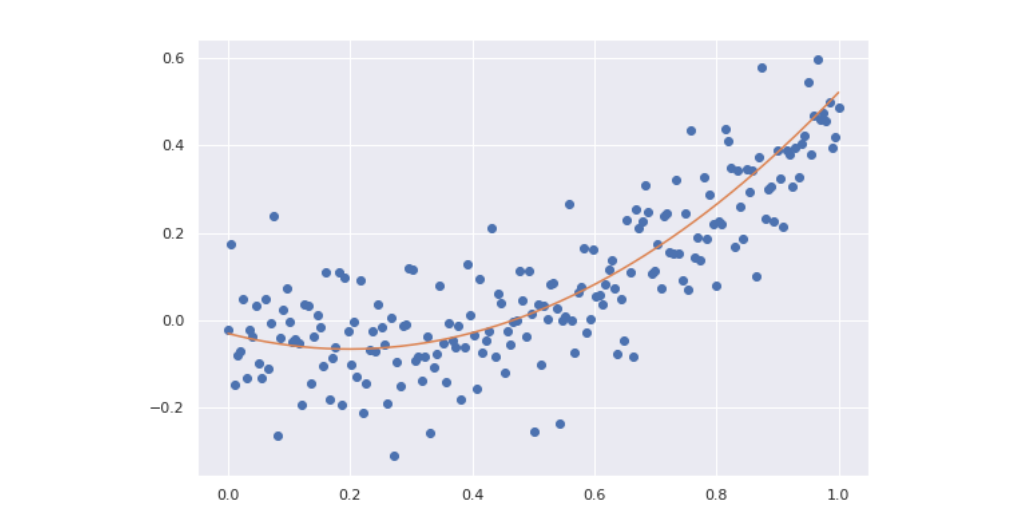
5.1.1 Regressione polinomiale a più variabili
Se la regressione prevede più attributi in input, ripetiamo il processo per ognuno degli attributi ed aggiungiamo anche i termini di interazione. Ad esempio, se la dimensione dell'input è 2 e si decide di polinomizzare la funzione aggiungendo gradi, allora i coefficienti totali saranno : È possibile ottenere i termini attraverso il teorema multinomiale. A causa della presenza dei termini di interazione, all'aumentare delle feature in input il numero di coefficienti da calcolare aumenta in maniera massiva e la computazione diventa onerosa. Se si effettua la regressione polinomiale con un grado molto alto è possibile incappare nel problema dell'overfitting.
Dal punto di vista procedurale, il modo più semplice per implementare la regressione polinomiale consiste nel dare in pasto ad un regressore lineare il numero finale di feature. Anziché costruire un regressore polinomiale per degli input che esegua la polinomizzazione al grado , potremmo (supposto ) utilizzare un regressore lineare mappando gli input originali ed ottenere lo stesso risultato.
5.1.2 Regolarizzazione
Limitando il grado della regressione polinomiale è possibile ridurre il rischio di overfitting. Tuttavia, a volte non si vuole rinunciare alla flessibilità di un polinomio di alto grado. Supponiamo che il problema di predizione sia risolto da un polinomio di grado 3, il cui secondo termine è mancante Il modello privato del secondo termine ha ridotto la propria capacità (meno coefficienti da calcolare) rispetto al modello che prende in considerazione i termini di ogni grado: Tale problema non può essere approssimato con un polinomio di secondo grado: Quindi utilizzeremo la prima soluzione, ponendo fissato. Computazionalmente è difficile determinare quale parametro deve essere posto a 0 per approssimare al meglio la soluzione del problema.
In generale esiste un rapporto tra la norma dei coefficienti di una funzione polinomiale e la sua flessibilità (e quindi capacità). Nel grafico sottostante vediamo tre polinomi i cui coefficienti sono proporzionali tra loro a meno dell'intercetta, scelta ad hoc per posizionare le funzioni vicine tra loro lungo l'asse . Il polinomio verde risulta visivamente meno flessibile, e concorde alla osservazione, i coefficienti sono più piccoli rispetto a quelli degli altri due polinomi.
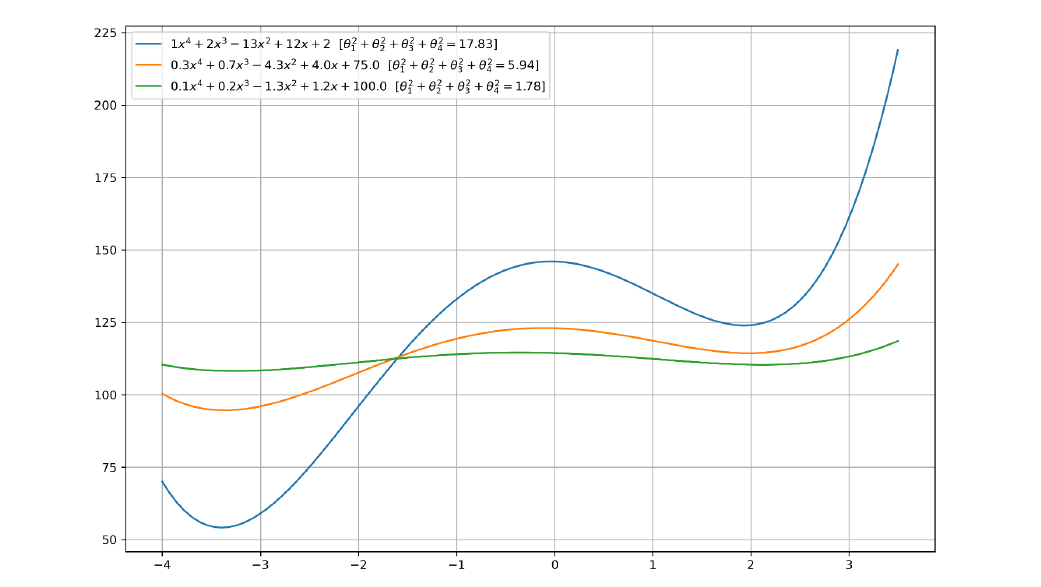
5.1.3 Termine di regolarizzazione
Se preferiamo trovare soluzioni meno flessibili per limitare la possibilità di overfitting, potremmo aggiungere alla funzione costo da minimizzare un certo termine, chiamato termine di regolarizzazione, che fornisce una misura di grandezza per i coefficienti del polinomio.
Il termine di regolarizzazione deve crescere proporzionalmente ai coefficienti, per cui possiamo utilizzare una semplice somma di quadrati: Il processo per cui la funzione costo viene modificata aggiungendo il termine di regolarizzazione per bilanciare la grandezza dei coefficienti è chiamato regolarizzazione. La funzione costo è ri-definita come segue: Dove il valore serve a bilanciare quanto la grandezza dei coefficienti influenzi la scelta dei coefficienti stessi. È un iperparametro da determinare attraverso un validation set. Questo tipo di regolarizzazione prende il nome di regolarizzazione L2 poiché il termine di regolarizzazione non è altro che la norma L2. Il tipo di regressione considerata prende il nome di Ridge regression.
5.1.4 Decadimento del peso
La nuova funzione costo è ancora differenziabile rispetto ai parametri , il che è fondamentale per l'implementazione di un algoritmo di discesa del gradiente. Lo step di aggiornamento sarà adesso: Notiamo che: Per cui scriviamo lo step di aggiornamento come segue: L'aggiornamento è analogo al precedente a meno di un fattore penalizzante , Questa regolarizzazione è anche chiamata decadimento del peso (weight decay) per indicare che i coefficienti (pesi) debbano decadere con il tempo per limitare la crescita.
6. Regressione logistica
Un regressore lineare multiplo permette di associare un numero reale ad un vettore in input attraverso una funzione parametrica . L'obiettivo di un classificatore è simile: predire una classe a partire da un vettore in input . Vedremo come è possibile costruire una funzione parametrica che possa performare la classificazione .
6.1 Limiti della regressione lineare per la classificazione
Ci concentreremo sul task della classificazione binaria per iniziare, quindi avremo due sole classi . Potremmo provare ad utilizzare la regressione lineare per predire direttamente la classe binaria: Tuttavia questo metodo risente di alcuni problemi fondamentali. Consideriamo un esempio ad una dimensione in cui degli input sono classificati in due classi :
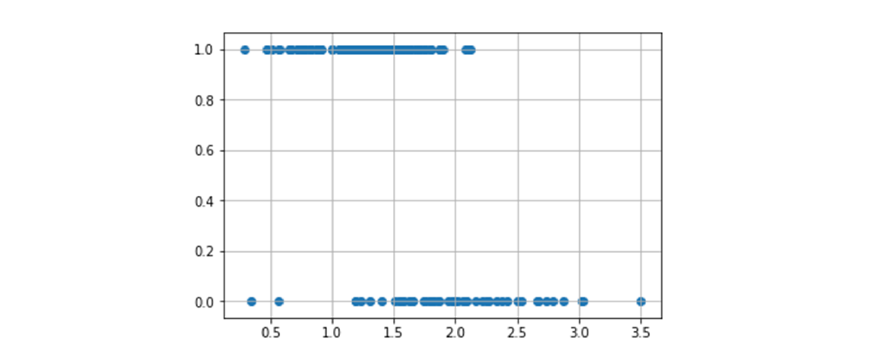
Idealmente vorremmo una funzione che associ tutti i punti "positivi" ad 1 e tutti i punti "negativi" a 0. Tale funzione sarebbe definita come , quindi il codominio sarà discreto. Se proviamo ad utilizzare la regressione lineare, otterremo con molta probabilità una linea del genere:
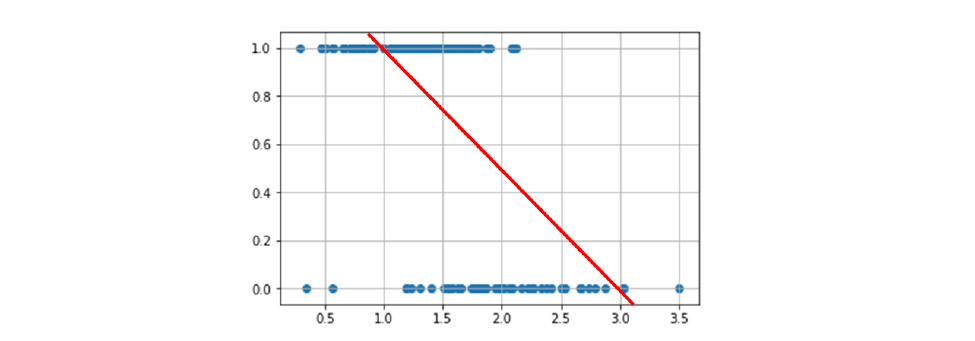
Possiamo vedere immediatamente che tale funzione non risultà essere particolarmente accurata nella classificazione: cosa fare quando i punti stanno nel mezzo? O quando stanno sopra 1 / sotto 0? Potremmo migliorare la funzione mappando gli input alla probabilità che essi assumano il valore 1: . La funzione sarebbe definita come segue: , che risolve i problemi sull'assegnazione dei valori tra 0 ed 1, ma risulta ancora imprecisa per input fuori dal range. Anziché una retta, vorremmo utilizzare una curva ad che copra gli elementi come segue:
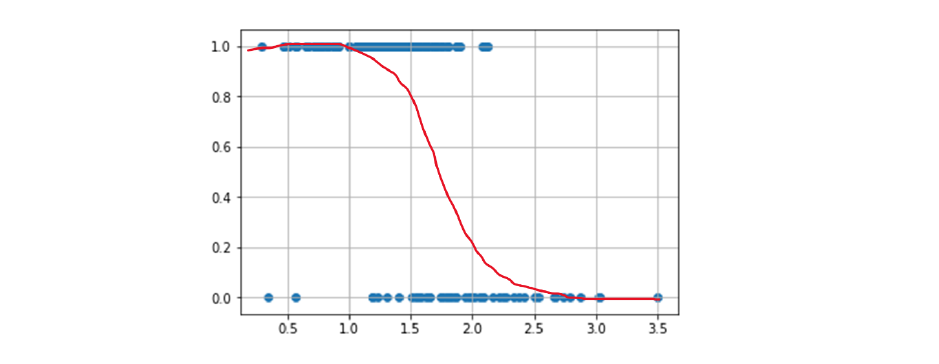
Questa funzione ideale mappa gli input nel range e satura a ed , il che è naturale poiché all'avvicinarsi ad uno dei due estremi densi aumenta anche la certezza di appartenenza ad una classe. Questa analisi suggerisce che non è possibile risolvere il problema della classificazione attraverso una funzione lineare.
6.2 Funzione dispari e Logit
Vorremmo trovare una trasformazione della probabilità che mappi i valori da a e che renda possibile l'approssimazione delle probabilità attraverso una funzione lineare.
Sia la probabilità che un esempio sia positivo. Considereremo la funzione dispari (odd function) di la misura della proporzione tra probabilità che l'esempio sia positivo e quella che l'esempio sia negativo: Questa prima trasformazione risolve parte del problema, di fatto mappa la probabilità dall'intervallo all'intervallo ). Vediamo l'effetto della mappatura nel grafico sottostante:
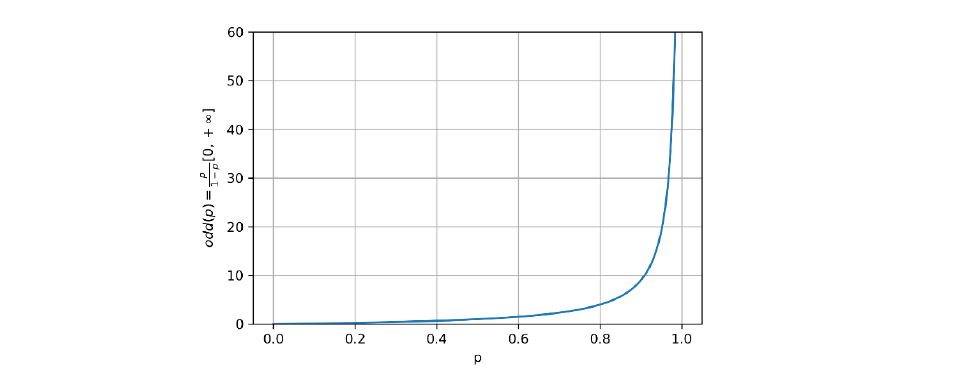
Vogliamo che l'intervallo finale sia , per cui definiamo la funzione logit come il logaritmo naturale della funzione dispari: Osserviamo che: altresì confermato dal grafico della funzione:
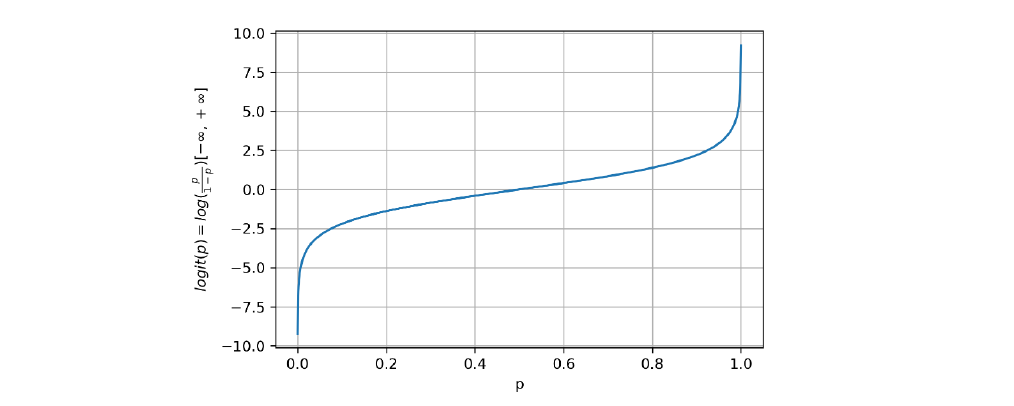
Ci si aspetta che le probabilità siano pressoché non lineari (a forma di ), la funzione di logit permette di linearizzare i dati rispetto all'asse , come mostrato in figura:
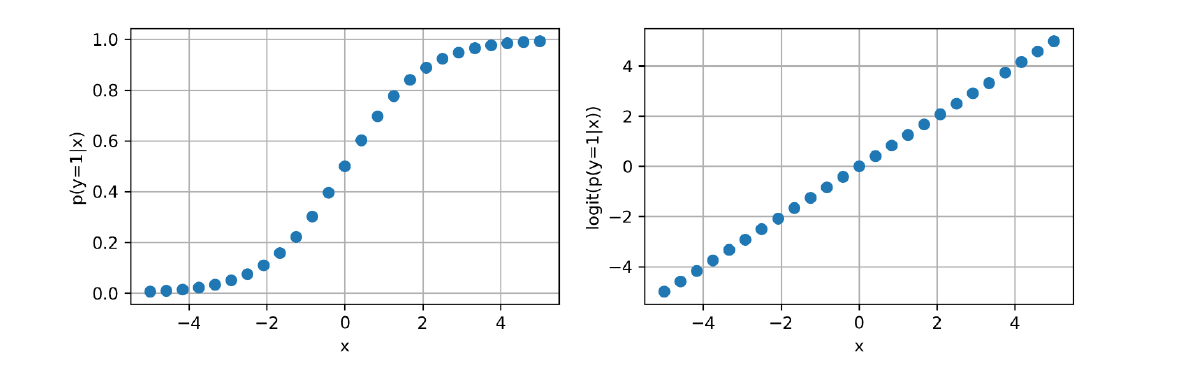
6.3 La funzione logistica
Adesso che la funzione logit mappa le probabilità in uno spazio in cui si dispongono linearmente, possiamo utilizzare un regressore lineare per trovare una retta che approssimi la funzione: Una volta trovati i coefficienti per il regressore lineare, dobbiamo trovare il metodo per estrapolare la probabilità dai risultati della funzione logit, quindi effettuare una mappatura inversa a quella iniziale: .
Possiamo farlo invertendo la funzione logit come segue:
- partiamo dalla espressione iniziale:
- utilizziamo l'esponenziale:
- moltiplichiamo entrambi i termini:
- semplifichiamo:
- raccogliamo per la probabilità:
- estraiamo la probabilità: Possiamo effettuare ulteriori semplificazioni una volta estratta la probabilità: La funzione derivata prende il nome di funzione logistica o funzione sigmoide ed è definita in generale come segue: La curva disegnata dalla funzione logistica è a forma di (da cui il nome sigmoide) come mostrato in figura:
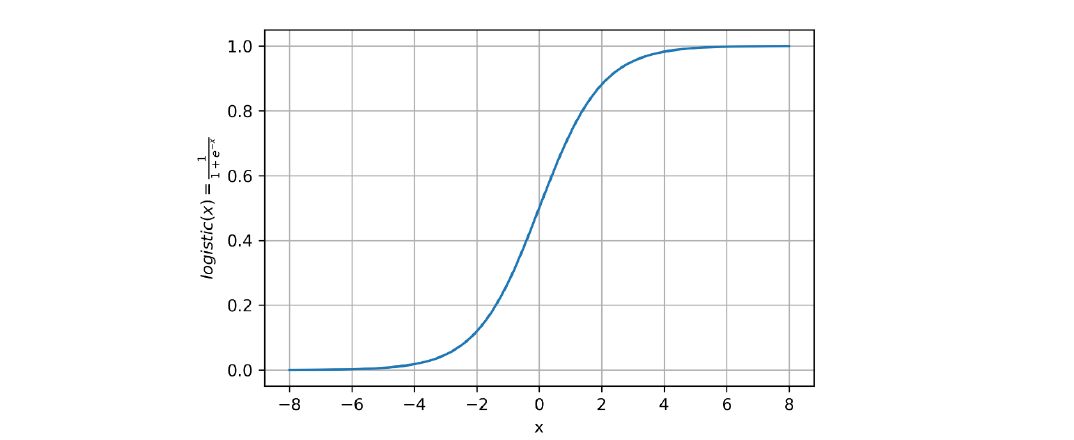
6.4 Il modello di regressione logistica
Possiamo finalmente definire il regressore logistico con la seguente funzione: Allenare il regressore logistico significa trovare i parametri che riescano ad approssimare al meglio la probabilita . La funzione approssimata non è più una retta, bensì un sigmoide:
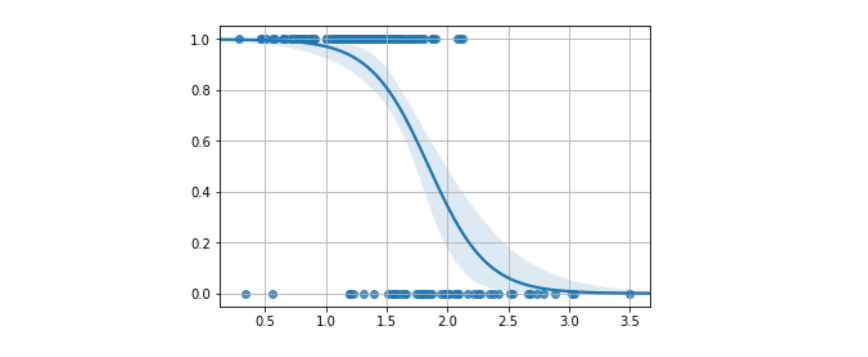
Una volta che il modello è allenato, possiamo classificare le osservazioni attraverso la seguente regola:
6.4.1 Funzione costo
Per allenare il modello definiremo una funzione costo, similmente a come fatto per la regressione lineare. Problema: il dataset fornisce degli input e degli output , questi ultimi sono interpretabili in termini probabilistici e non come risultati della funzione logistica, quindi non è possibile utilizzare direttamente la funzione costo del regressore lineare e stimare una retta.
Dalla definizione: Scriviamo: Per denotare l'utilizzo di un insieme di parametri . O nella versione compatta: Osservando che verrà preso in considerazione solo uno dei fattori a seconda se o . Possiamo stimare i parametri massimizzando la likelihood: Se assumiamo che tutte le osservazioni del training set sono indipendenti, allora la likelihood potrà essere espressa come segue: Massimizzare tale espressione è analogo a massimizzare il logaritmo negativo della likelihood (negative log likelihood, nll): Definiremo la funzione costo :
6.4.2 Applicare la discesa del gradiente
Possiamo ottimizzare la funzione costo del regressore logistico attraverso l'algoritmo di discesa del gradiente. Per farlo, è necessario applicare una funzione di aggiornamento del genere: È necessario quindi calcolare la derivata parziale della funzione costo . Si lascia allo studente volenteroso la derivazione, che risulta essere: Dove indica la funzione sigmoide (o logistica): Per cui il passo d'aggiornamento sarà esplicitato come segue: Osserviamo che il passo di aggiornamento è analogo a quello della regressione lineare a meno della funzione rimpiazzata con la funzione sigmoide .
6.4.3 Interpretazione geometrica
A differenza della regressione lineare multipla, che trova l'iperpiano che approssima al meglio i dati, la regressione logistica trova l'iperpiano che separa al meglio i dati. Come vediamo nell'esempio bidimensionale.
Ipotizziamo di allenare un regressore logistico con i seguenti dati: Supponiamo che l'insieme di coefficienti risultante sia il seguente: Per capire come i dati sono classificati analizziamo il caso di massima incertezza, ovvero quando la probabilità risultate è del 50% per ambo le classi: Se esplicitiamo l'ultima equazione otteniamo: Per cui il coefficiente angolare è e l'intercetta è . Se grafichiamo questa linea, otteniamo il confine decisionale tra gli elementi delle due classi.
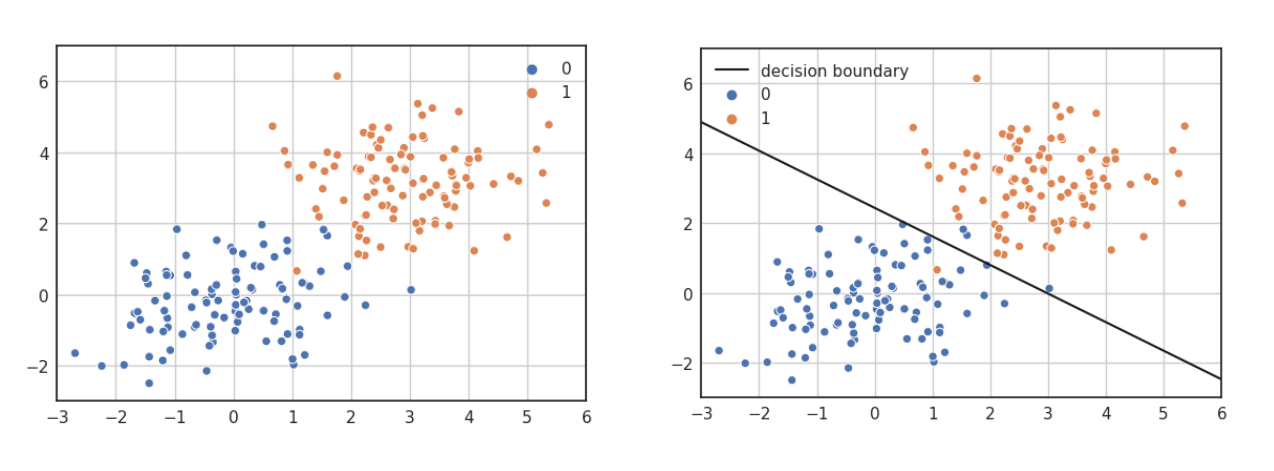
* L'iperpiano rappresentato è dato dai coefficienti e non rappresenta la funzione logistica, che non è una retta, bensì una curva.
6.4.4 Estensione al caso multiclasse: metodo one-vs-all
È possibile estendere il metodo della regressione logistica attraverso varie tecniche, tra cui la one vs all, la one vs one e la softmax regression. Vedremo in particolare come funziona la one vs all.
L'approccio one-vs-all permette di trasformare il problema della classificazione multiclasse (con più di 2 classi) in un insieme di problemi di classificazione binaria. Ogni sottoproblema può essere risolto attraverso un classificatore binario (es. il regressore logistico). Oltre al classificatore binario, è necessario che l'output contenga anche un valore di confidenza (confidence value), come un probabilità. Questo è necessario per confrontare i risultati di tutti i classificatori e capire quale potrebbe essere quello corretto.
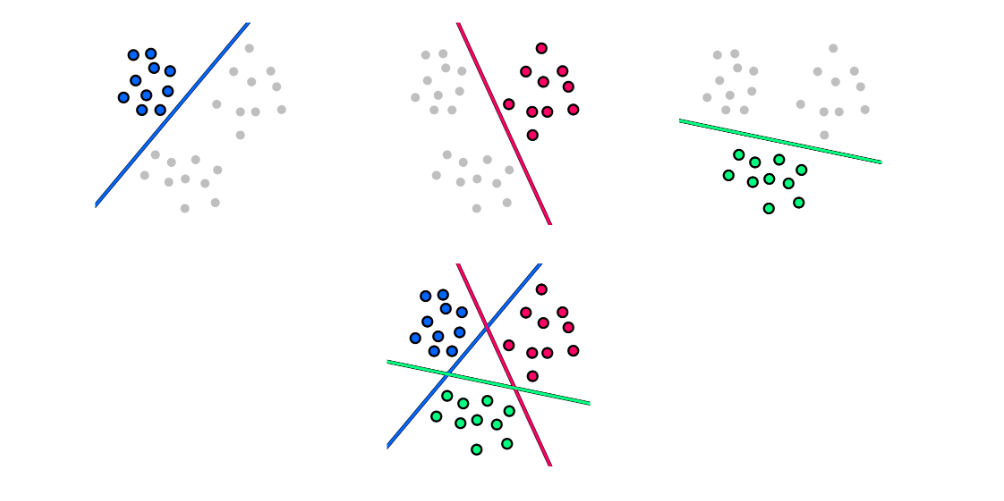
Dato un problema di classificazione con classi, l'approccio one-vs-all consiste nei seguenti passi:
- Dividere in task di classificazione binaria , dove si considera la classe contro tutte le altre.
- Allenare i classificatori separatamente.
- Per classificare un input utilizziamo ognuno dei classificatori , poi assegniamo la classe del classificatore con il confidence value maggiore.
Reti e modelli random
1. Reti
Le reti (o grafi) sono il modello matematico che permette di codificare le interazioni tra le componenti di un sistema complesso. La scienza che studia le reti prende il nome di network science. Formalmente, un grafo è una coppia dove è l'insieme di vertici ed è l'insieme degli archi, dove un arco è una coppia di vertici . I vertici rappresentano le componenti del sistema, mentre gli archi rappresentano le interazioni tra le componenti. Se allora diremo che è adiacente ad .
Quando si parla di network (reti) si fa spesso riferimento a sistemi reali, come le social network o il web. In tale contesto si parla di nodi e link tra nodi. Una network viene rappresentata matematicamente da un grafo, dove si usano in maniera formale i termini "vertici" o "archi" .
1.1.1 Grafi diretti e indiretti
Un grafo è detto indiretto (o non orientato) se: Altrimenti si parla di grafo diretto (o orientato). In altre parole, in un grafo indiretto ogni interazione tra due nodi è reciproca, mentre nelle reti dirette non è detto che lo sia.
1.1.2 Grafi pesati ed etichettati
Ai nodi e agli archi di una rete possono essere associate delle informazioni aggiuntive legate alla semantica della rete stessa. Se le informazioni associate ai nodi / archi sono valori numerici (interi o reali) si parla di rete pesata. Se sono etichette o stringhe si parla di grafo etichettato.
1.1.3 Grafi bipartiti
Un grafo bipartito è un grafo in cui i nodi costituiscono due insiemi disgiunti e e ciascun arco del grafo collega un nodo di ad un nodo di . Non esistono archi che collegano tra loro nodi dello stesso insieme.
A partire da una rete bipartita è possibile generare due reti chiamate proiezioni del grafo, una rispetto all'insieme e l'altra rispetto all'insieme . La proiezione rispetto ad è un grafo i cui nodi sono i nodi di ed un arco collega due nodi se e solo se hanno almeno un adiacente in comune nel grafo bipartito. Definizione analoga per la proiezione rispetto a .
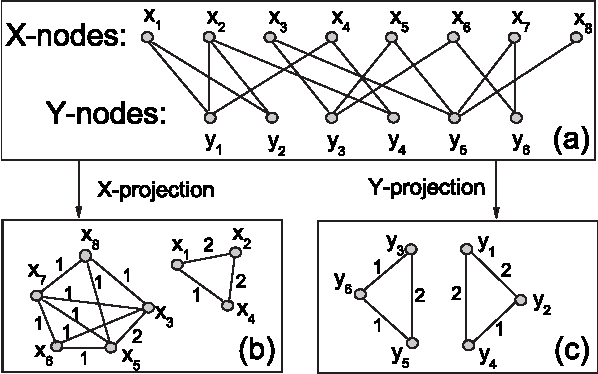
In una proiezione è possibile specificare, in un arco tra due nodi, quante connessioni hanno in comune i due nodi. Altrimenti è possibile considerare un multigrafo e aggiungere un arco tra e per ogni nodo in comune nel grafo bipartito.
1.1.4 Altre tipologie di grafi
- Grafo multipartito: generalizzazione del grafo bipartito, con più insiemi disgiunti di nodi.
- Grafo con self-edge (o self-loop): grafo che ammette archi che partono e arrivano allo stesso nodo.
- Multigrafo: grafo che ammette più archi tra e .
- Grafo multilayer: un grafo con più layer che permette connessioni sia all'interno che all'esterno del layer.
- Grafo multiplex: grafo multilayer in cui i nodi non possono connettersi con nodi di altri layer.
Le reti multiplex e multilayer sono molto utilizzate nel contesto della deanonimizzazione.
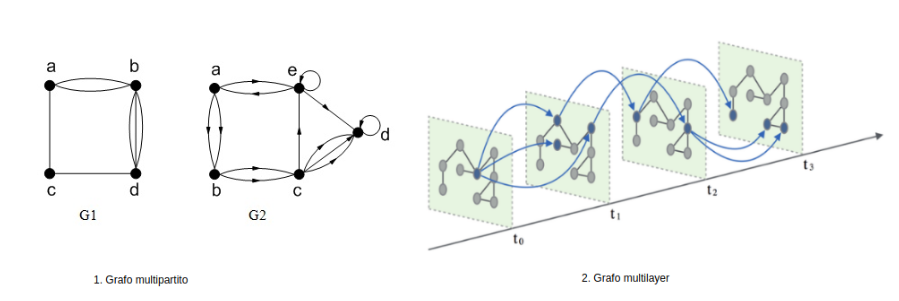
1.1.5 Grafo completo o Clique
Un grafo completo, o Clique, è un grafo in cui tutte le coppie distinte tra loro sono collegate da un arco. Il numero massimo di archi in un grafo non direzionato con nodi è dato dalle combinazioni a due a due dei nodi: Il grado medio di un grafo completo con nodi è banalmente (ogni nodo è connesso con tutti i nodi, meno che con se stesso).
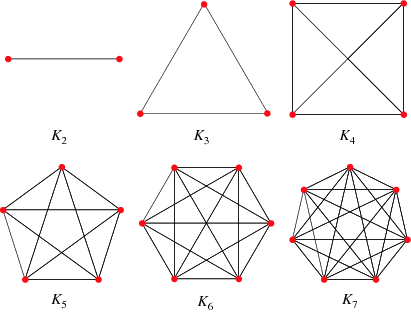
1.1.6 Grado di un nodo e grafo regolare
Il grado (degree) di un nodo è il numero di nodi adiacenti ad nel grafo. Un nodo con grado 0 è detto isolato. In un grafo diretto si fa distinzione tra:
- Grado uscente del nodo : numero di nodi adiacenti ad nel grafo
- Grado entrante del nodo : numero di nodi a cui è adiacente.
- Grado totale del nodo : somma del grado uscente e del grado entrante.
Un grafo è detto regolare se ogni nodo ha lo stesso grado.
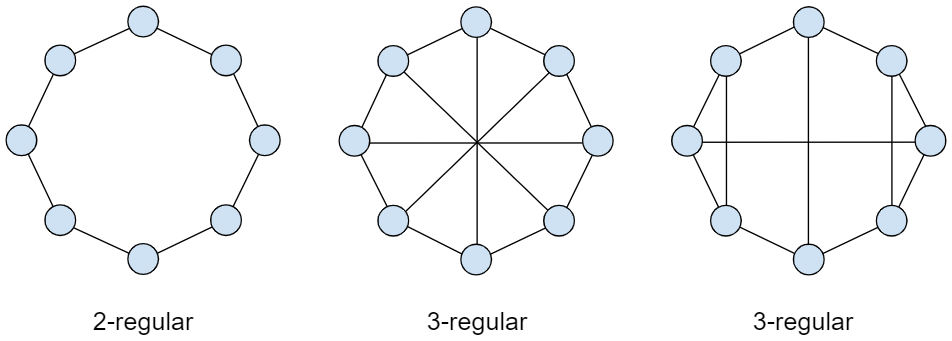
1.1.7 Grado medio
Il grado medio della rete in un grafo indiretto è Poiché ogni arco nell'insieme sarà bidirezionale. Invece in un grafo diretto avremo Quindi vale sempre , poiché gli archi uscenti di un nodo saranno archi entranti di un altro nodo.
1.1.9 Rappresentazione di un grafo
È possibile rappresentare un grafo con nodi attraverso una matrice di adiacenza di dimensione , dove l'elemento se esiste un arco da a , altrimenti. Se il grafo è pesato, allora la matrice riporterà il peso dell'arco tra e nell'elemento , 0 altrimenti.
Questa rappresentazione risulta poco conveniente in termini di spazio, poiché un nodo è spesso collegato a pochi altri nodi della rete. Una rappresentazione più efficiente risulta essere la lista di adiacenza, dove ad ogni nodo è appesa la lista di nodi adiacenti ad esso, o anche la lista di archi.
1.2 Cammini tra nodi
Un cammino tra due nodi e è definito come una sequenza ordinata di archi:
In generale, possono esserci più cammini tra due nodi generici. Definiamo:
- Lunghezza del cammino: la quantità di archi
- Cammino minimo: cammino di lunghezza minima
- Distanza: lunghezza del cammino minimo
- Diametro di : massima distanza tra due nodi in
Definiamo ciclo un cammino in cui nodo di partenza e nodo finale coincidono: Un ciclo di lunghezza 1 è detto cappio o self-loop. Un grafo che non contiene cicli è detto aciclico, o anche albero.
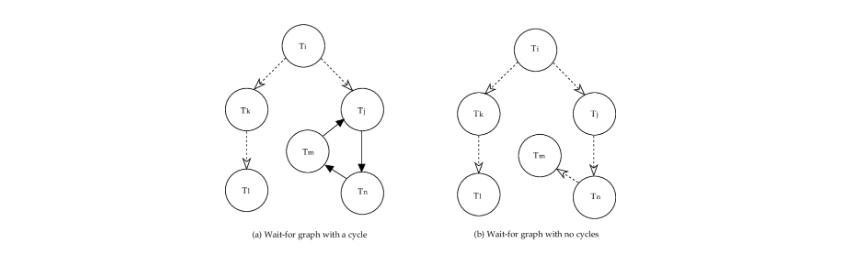
1.2.1 Connettività di un grafo
Due nodi e si dicono connessi se esiste un cammino tra essi, altrimenti si diranno disconnessi. Un grafo si dice connesso se tutte le coppie di nodi sono connesse, disconnesso altrmenti. Un grafo disconnesso risulta formato dall'unione di due o più sottografi connessi, chiamati componenti. Un sottografo è formato da un sottoinsieme di nodi di e dagli archi che li collegano.
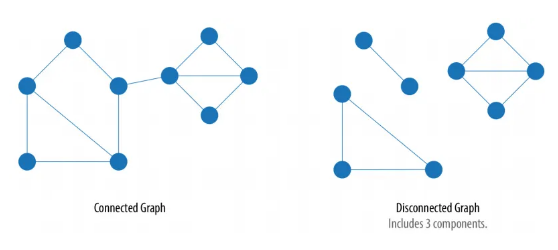
Per i grafi diretti o orientati si parla di connettività forte o debole. Un grafo orientato è detto fortemente connesso se, per ogni coppia di nodi esiste un cammino tra e in . È invece detto debolmente connesso se, per ogni coppia di nodi , esiste un cammino tra e in , oppure esiste un cammino nel grafo ottenuto da sostituendo gli archi direzionati con archi non direzionati. Da queste definizioni derivano, in maniera analoga a prima, i concetti di componente fortemente connessa e componente debolmente connessa.
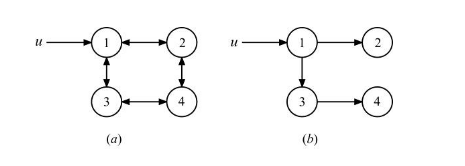
Definiamo arco ponte (bridge) quell'arco che, se cancellato, trasforma un grafo connesso in un grafo disconnesso. Chiamiamo punto di articolazione (hub) quel nodo che, se cancellato, trasforma un grafo connesso in un grafo disconnesso. Chiamiamo componente connessa gigante la componente connessa più grande.
1.3 Descrivere una rete
È possibile descrivere una rete attraverso le sue proprietà, come la distribuzione dei gradi , la lunghezza media dei cammini , o il coefficiente di clustering .
1.1.8 Distribuzione dei gradi
La distribuzione dei gradi è una distribuzione di probabilità, dove rappresenta la probabilità che un generico nodo della rete abbia grado . La distribuzione dei gradi è la proprietà più importante della rete, poiché fenomeni come la robustezza della rete o la diffusione dei virus si possono spiegare attraverso tale proprietà. Data una rete reale, si ottiene dividendo il numero di nodi con grado per il numero di nodi della rete.
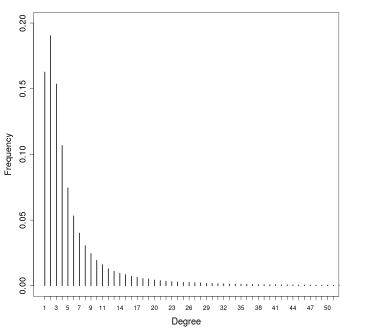
1.3.1 Coefficiente di clustering
Il coefficiente di clustering di un nodo è una misura di quanto gli adiacenti di siano connessi tra loro. Essendo il grado del nodo, allora vi saranno nodi adiacenti ad . Il numero massimo di archi possibili tra nodi è dato dalla formula precedentemente studiata: Definiamo il numero di archi effettivamente esistenti tra i adiacenti ad . Definiamo il coefficiente di clustering come il rapporto tra il numero di archi esistenti ed il numero di archi possibili: In altre parole, il coefficiente di clustering misura la densità locale della rete in un nodo : più densamente interconnesso è il vicinato di , più alto è il coefficiente di clustering.
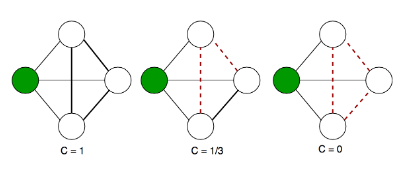
Definiamo coefficiente di clustering medio la media dei coefficienti di clustering di tutti i nodi della rete:
Il concetto di coefficiente di clustering globale è basato su triple di nodi. Una tripla consiste di tre nodi connessi da due (tripla aperta) o tre (tripla chiusa) collegamenti. Ogni tripla è incentrata su un nodo. Un triangolo consiste di tre triple chiuse incentrate sui tre stessi nodi che lo compongono (clique con 3 nodi). Definiamo coefficiente di clustering globale il rapporto tra il numero di triangoli della rete (clique con 3 nodi) ed il numero totale di triple di nodi.
1.3.2 Numero di cammini
Supponiamo di voler calcolare il numero di cammini di lunghezza tra e . Se cerchiamo cammini di lunghezza , allora basta consultare la matrice di adiacenza e vedere se l'elemento sia asserito. Se cerchiamo cammini di lunghezza , allora dobbiamo considerare un qualsiasi altro nodo che li connetta, per cui: In generale, il numero di cammini tra e di lunghezza è È possibile effettuare questa analisi attraverso una catenia di Markov, in cui la matrice di adiacenza (normalizzata) corrisponde alla matrice di transizione.
1.3.3 Lunghezza media dei cammini
La lunghezzza media di un cammino per un grafo connesso (o una componente) o una componente fortemente connessa di un grafo diretto, corrisponde a Il valore indica la distanza tra i nodi e . Normalizziamo per il numero massimo di archi perché vogliamo indicare tutti i possibili cammini, e dividiamo per due per evitare di considerare due volte lo stesso cammino (nel caso di grafi indiretti).
1.4 Centralità di un nodo
La centralità è una misura dell'importanza di un nodo nella rete. Esistono diverse misure di centralità, a seconda del criterio utilizzato per misurare l'importanza di un nodo.
1.4.1 Degree centrality
La centralità basata sul grado è la misura più semplice di centralità. La degree centrality è semplicemente il grado del nodo. Più alto è il grado del nodo e più è importante.
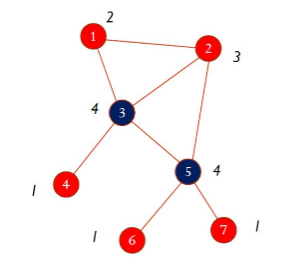
1.4.2 Betweenness centrality
La betweenneess centrality è basata sul concetto di betweenness di un nodo: dato un nodo e due nodi qualsiasi del grafo e , si calcola , ovvero la frazione di cammini minimi tra e che passano per . La betweenness di è ottenuta sommando per tutte le coppie
Dove è il numero di cammini minimi da a , mentre indica quanti di questi contengono il nodo . Usualmente, tale metrica si normalizza come: Dove al denominatore si ha il coefficiente binomiale che specifica il numero di cammini possibili tra gli nodi restanti nella rete. In base a questa definizione, un nodo è centrale se si trova nel mezzo di molti cammini di comunicazione tra nodi del grafo.
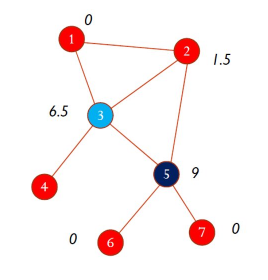
1.4.3 Closeness centrality
La closeness centrality si basa sulla vicinanza media di un nodo rispetto a tutti gli altri nodi del grafo. Dato un nodo , si calcola la lunghezza media dei cammini minimi da agli altri nodi del grafo. La closeness centrality di è definita come il reciproco di .
La closeness centrality di un nodo è una misura della velocità media con cui una informazione, partendo da , può raggiungere tutti gli altri nodi del grafo.
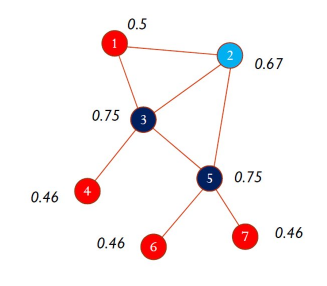
1.4.4 PageRank centrality
La PageRank centrality si basa sull'osservazione che le connessioni di un nodo con gli altri nodi non hanno tutte lo stesso valore (come assunto invece dalla degree centrality). Connessioni a nodi con elevato grado hanno un peso maggiore rispetto a connessioni a nodi di grado minore.
È possibile definire la metrica ricorsivamente: un nodo è tanto più importante quanto più è connesso ad altri nodi importanti della rete. Formalmente, il Page Rank di un nodo , , è dato da: Dove è l'insieme dei nodi che hanno come adiacente e è il grado uscente di .
1.5.5 Calcolo del PageRank
Consideriamo un semplice esempio di rete diretta costituita da 4 nodi . Immaginiamo che ogni nodo abbia a disposizione un tesoro iniziale, uguale per tutti. Se il tesoro iniziale complessivo è pari ad 1, ogni nodo avrà un tesoro iniziale pari a 0.25.
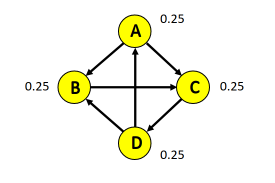
Ogni nodo deve cedere il proprio tesoro in parti uguali tra i suoi adiacenti. Calcoliamo ad esempio il tesoretto di :
- cede metà del suo tesoro a B e a C. Dunque B riceve 0.125 da A, ovvero o .
- non cede nulla a B.
- cede metà del suo tesoro a B e ad A. Dunque B riceve 0.125 da D, ovvero o .
Quindi: Con lo stesso principio possiamo calcolare il nuovo page rank degli altri 3 nodi. Alla fine del primo round è l'unico nodo che si ritrova con un tesoro maggiore.
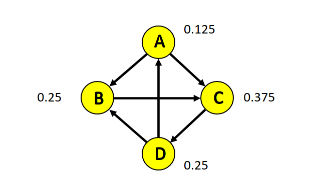
Iterando questo scambio di tesori si otterrà una situazione di equilibrio in cui il tesoro di ogni nodo non varierà più in maniera significativa. A tempo di convergenza si conosce il valore di centralità per ogni nodo.
2. Modelli random
Uno degli obiettivi della Network science è quello di costruire modelli in grado di riprodurre proprietà specifiche della rete reale, legate ad esempio al grado dei nodi, al diametro della rete etc. Le reti reali, a parte qualche rara eccezione (es. reticoli), non hanno una struttura regolare, ma presentano una certa randomicità. Sin dagli anni '50 sono stati teorizzati e sviluppati modelli probabilistici, detti modelli random, per cercare di spiegare queste proprietà intrinseche delle reti reali. Tali modelli sono generativi, cioè permettono di generare reti con certe caratteristiche.
Supponiamo di avere un modello random che generi una rete con le stesse caratteristiche delle reti reali. Supponiamo anche di stare analizzando una rete reale e di ottenere certi risultati (es. coefficiente di clustering, distribuzione dei gradi etc). Per capire se la rete reale ha proprietà attese o sorprendenti, essa va confrontata (quindi sottoposta a test di ipotesi) con delle reti generate da un modello random nullo che riesca a catturare le proprietà delle reti reali.
2.1 Modello di Erdos-Renyi
Il primo modello random fu proposto da due matematici ungheresi, Erdos e Renyi, negli anni '60 e prende il loro nome. Fissata una probabilità ed il numero di nodi della rete da generare, il modello Erdos-Renyi crea un insieme iniziale di nodi isolati e per ciascuna coppia di nodi distinti, aggiunge un arco con probabilità . La rete ottenuta con il modello Erdos-Renyi è detta grafo random o rete di Erdos-Renyi.
2.1.1 Variante G(N,L) del modello
Il modello appena descritto è detto modello , perché genera un grafo random partendo dal numero di nodi e dalla probabilità che esista un arco tra due nodi. Una variante è rappresentata dal modelo , in cui si genera un grafo random con nodi ed archi random.
In questa variante si parte da una rete con nodi isolati. Ad ogni passo si sceglie una coppia non connessa e casuale e si aggiunge un arco tra essi. Si prosegue sinché la rete non contiene archi. I due modelli sono equivalenti tra loro.
2.1.2 Distribuzione dei gradi (e degli archi)
Per ricavare l'espressione della distribuzione dei gradi di una rete random con nodi, occorre calcolare la probabilità che un generico nodo abbia grado . Ipotizziamo di essere al turno di assegnazione degli archi di generico nodo , la probabilità che abbia grado è la probabilità che su nodi rimanenti, nodi si colleghino ad . Tale distribuzione prende il nome di distribuzione binomiale ed è definita per i generici e come segue:
Nel nostro caso e , per cui:
Dove è la probabilità che nodi restanti non creino un collegamento con , mentre è la probabilità che nodi si colleghino ad . Il coefficiente binomiale iniziale prende in considerazione tutti i modi in cui è possibile selezionare nodi da collegare ad tra gli rimanenti. Avendo associato la distribuzione dei gradi ad una binomiale, è possibile calcolare il valore atteso
Banalmente poiché una variabile binomiale è data dalla somma di variabili Bernoulliane, il cui valore atteso è . Allo stesso modo si può dimostra che la varianza rispetto al grado medio corrisponde a
Allo stesso modo, è possibile dimostrare che la probabilità che una rete random abbia esattamente archi totali è distribuita secondo una binomiale:
Con valore atteso e varianza .
Per la distribuzione binomiale è ben approssimata da una distribuzione di Poisson:
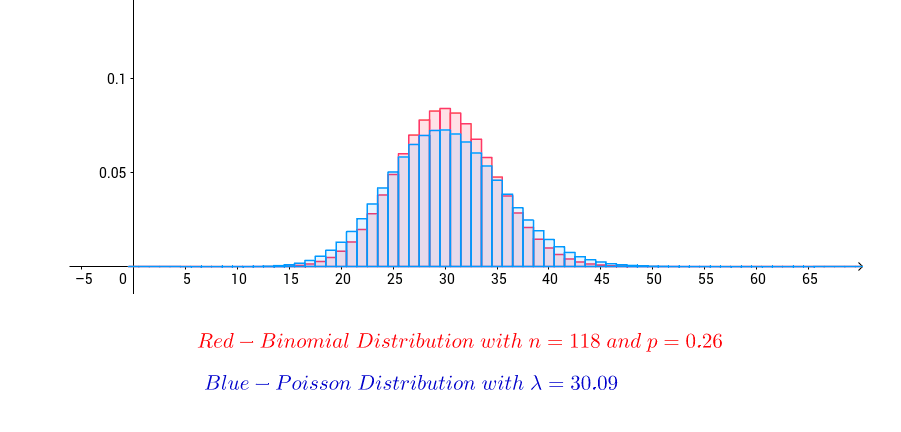
Dal momento che la distribuzione dei gradi è binomiale, in una rete random i nodi hanno perlopiù lo stesso grado. In reti random grandi, in cui la distribuzione è approssimativamente di Poisson, la maggior parte dei nodi ha un grado più o meno pari al grado medio . Pochi nodi hanno un grado diverso dalla media.
2.1.3 Coefficiente di clustering nel grafo random
Per calcolare il coefficiente di clustering di un generico nodo , occorre prima stimare il numero atteso (media) di archi tra gli adiacenti di . Se è il grado di , il numero atteso di archi è: Dunque, il coefficiente di clustering di è dato da: Dato che allora: Quindi il coefficiente di clustering è inversamente proporzionale al numero di nodi nella rete e direttamente proporzionale al grado medio. Si noti che il coefficiente di clustering del nodo è indipendente dal grado del singolo nodo. Considerazioni analoghe possono essere fatte per il coefficiente di clustering globale.
2.1.4 Definizione di espansione
Un grafo ha una espansione se si ha
\text{#archi uscenti da $S$} \ge \alpha \min(|S|, |V \setminus S|)
o alternativamente
\alpha = \min_{S \subseteq V} \frac {\text{#edges leaving $S$}} {\min(|S|, |V \setminus S|)}
L'espansione misura la robustezza della rete: per disconnettere nodi è necessario rimuovere un numero maggiore o uguale ad archi.
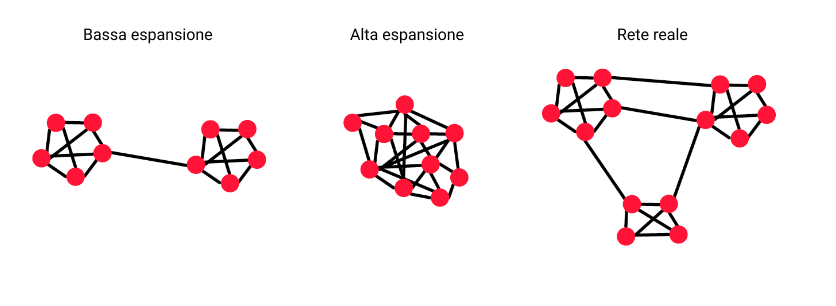
Teorema n.1
Sia un grafo random regolare di grado 3 con nodi, allora esiste una costante ed indipendente da tale che l'espansione del grafo è sempre maggiore o uguale ad .
Teorema n.2
Sia un grafo con nodi e con espansione , allora per tutte le coppie di nodi e esiste un cammino con archi che li connette.
2.1.4 Lunghezza dei cammini e fenomeno small world
Dati i teoremi precedenti, possiamo affermare che la distanza (o lunghezza dei cammini minimi) tra due generici nodi e è . È possibile dimostrare che: Dal momento che , nella rete random le distanze tra i nodi della rete sono mediamente piccole, tale fenomeno prende il nome di small world. Il termine: implica che più è densa la rete, più piccola è la distanza tra i nodi.
2.1.5 Confronto tra reti reali e reti random
Prendiamo come esempio la rete MSN, ovvero una rete reale che rappresenta i collegamenti tra gli utenti in Microsoft Messenger. Confrontiamo le proprietà di tale rete con una rete generata da un modello di Erdos-Renyi. Iniziamo con la distribuzione dei gradi: osserviamo che le due distribuzioni differiscono. Le reti reali assumono una distribuzione dei gradi molto simile ad una esponenziale (non lo è) che studieremo più avanti.
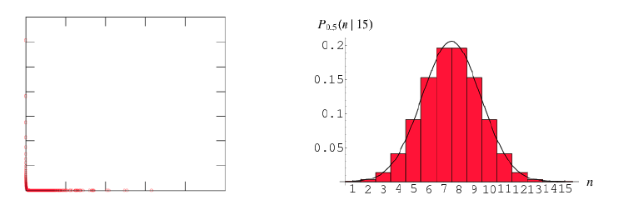
La distanza media tra due nodi nella rete MSN è ; il modello random riproduce tale proprietà con un valore medio di circa (). Il coefficiente di clustering differisce nelle due reti, con un valore di 0.11 per la rete MSN ed un valore vicino allo 0 per la rete random. Possiamo affermare che le reti reali sono diverse dalle reti random.
2.1.6 Proprietà riprodotta: small-world
L'unica proprietà delle reti reali che la rete random riesce a cogliere abbastanza bene è quella denominata "small world", legata alla distanza media tra i nodi (anche se spesso nelle reti reali si osserva una distanza ancora più bassa). Il fenomeno small world afferma che anche due individui che vivono in zone molto lontane sulla Terra possono essere connessi tra loro attraverso una catena molto piccola di conoscenze. Tale fenomeno è conosciuto anche con il termine "sei gradi di separazione" (six degrees of separation). La teoria dei sei gradi di separazione fu formulata per la prima volta nel '29 dallo scrittore ungherese Frigyes Karinthi, ma il termine "sei gradi di separazione" fu coniato in seguito ad un famoso esperimento condotto nel '67 da uno psicologo americano, Stanley Milgram.
L'esperimento di Milgram
Milgram selezionò in maniera casuale un gruppo di studenti americani del Midwest e chiese loro di spedire un pacchetto ad un estraneo del Massachusetts, a migliaia di chilometri di distanza. Ad ognuno di questi studenti Milgram consegnò una lettera con indicazioni riguardo il nome del destinatario, il suo impiego e la zona di residenza, senza però specificare l’indirizzo esatto. Ad ogni partecipante all’esperimento fu quindi chiesto di spedire il proprio pacchetto ad una persona da loro conosciuta che, a loro giudizio, potesse avere maggiori probabilità di conoscere il destinatario finale. Quella persona avrebbe fatto a sua volta lo stesso, fino a quando il pacchetto non fosse arrivato a destinazione. Al termine dell’esperimento, Milgram scoprì con sorpresa che il numero medio di intermediari era 5.2, quindi un numero piccolo e molto vicino a quello teorizzato da Kharinty nel 1929. Ad oggi l'esperimento è stato riproposto e riconfermato attraverso le reti sociali ed altri tipi di reti digitalizzate.
Definizione di small-world
Formalmente, una rete soddisfa le proprietà small-world se la distanza media tra i nodi è: Ovvero, una rete è small-world se la distanza media tra i nodi ha una dipendenza logaritmica rispetto alla dimensione della rete (numero di nodi).
2.2 Modello Watts-Strogatz
Il modello Erdos-Renyi approssima bene la proprietà small-world, ma non il coefficiente di clustering della rete reale. Nel '98 Duncan Watts e Steven Strogatz proposero un'estensione al modello Erdos-Renyi, chiamato modello Watts-Strogatz o modello small-world.
Il modello consente di creare delle reti random che rappresentano una interpolazione tra il grafo regolare, che ha un alto coefficiente di clustering ma non esibisce la proprietà small-world, ed il grafo random, che ha basso coefficiente di clustering ma gode della proprietà small-world.
Anche in questo caso, la distribuzione dei gradi che si ottiene è simile ad una distribuzione di Poisson. Il tipo di grafo prodotto dipende da un parametro , detto anche parametro di rewiring. La rete che si ottiene ha caratteristiche intermedie tra la rete regolare e quella random: più basso è , più la rete è simile alla rete regolare, più è alto , più è simile alla rete random.
Sia il numero di nodi della rete da generare, il parametro di rewiring e un intero , siano gli identificativi dei nodi della rete. Si collega ciascun nodo ai nodi . Al termine di questo passo si ottiene un grafo regolare. Per ciascun arco, si scambia il nodo destinazione con un altro nodo random della rete con probabilità .
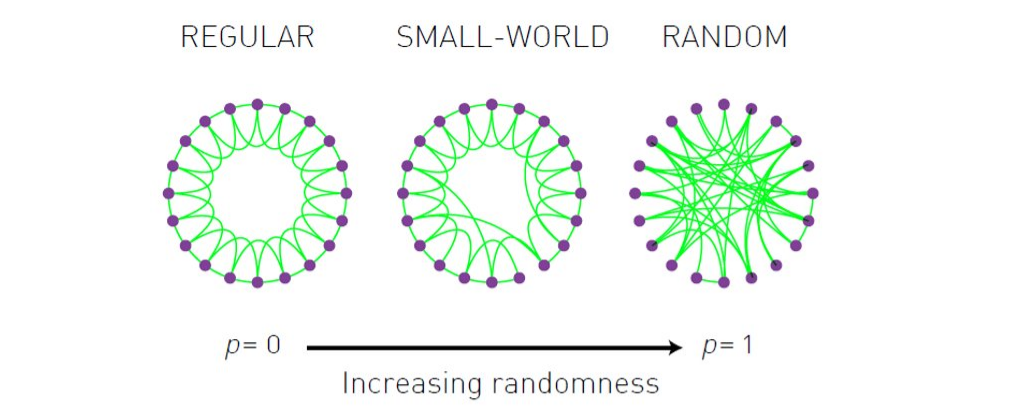
Plottando l'andamento del coefficiente di clustering e della distanza media tra nodi al variare del parametro , notiamo che il coefficiente di clustering decresce lentamente, mentre la distanza decresce più velocemente. È possibile travare una regione in cui il coefficiente di clustering sia ancora alto, mentre la distanza sia piccola (come indicato in foto). Il modello di Watts-Strogatz riesce a catturare due delle proprietà delle reti reali, tuttavia non riesce a riprodurre la distribuzione dei gradi.
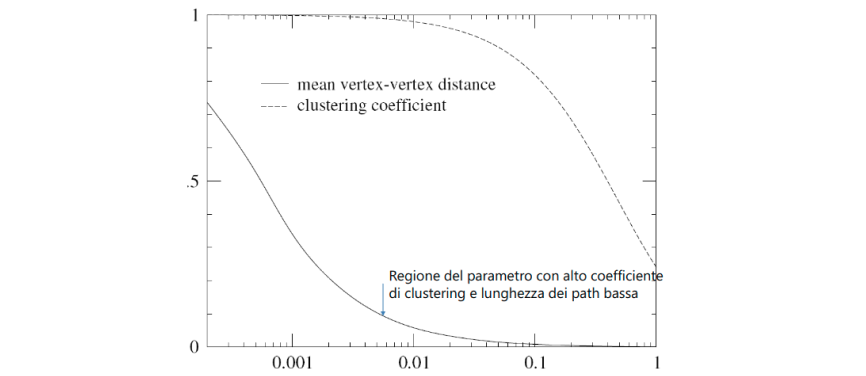
2.2.1 Problema della navigazione e modello di Kleinberg
Consideriamo il problema della consegna di un messaggio da un generico nodo della rete ad un generico nodo della rete. Avendo una visione globale della rete, trovare il cammino minimo che collega i due nodi risulta essere molto semplice. Le reti random small world, in questo caso, ci permettono di consegnare in messaggio in tempo . Tuttavia, quando non si dispongono di informazioni globali e vengono sfruttati algoritmi decentralizzati, pur avendo una distanza media logaritmica tra nodi, il tempo di navigazione può essere maggiore. La caratteristica della rete che descrive la capacità di arrivare da un nodo ad un altro nella rete senza informazioni globali è chiamata navigabilità.
Il modello di Kleinberg è una versione del modello di Watts-Strogatz che garantisce un tempo di navigazione . Supponiamo di disporre di una griglia di punti (lattice) e di misurare la distanza tra due punti attraverso la distanza di Manhattan.
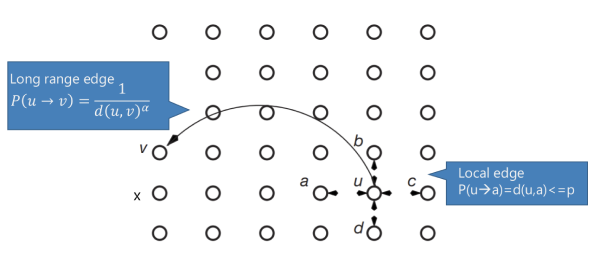
Definiamo arco locale (local edge) di un generico nodo , tutti gli archi che collegano a nodi con distanza di Manhattan pari ad 1. Gli archi locali esistono con probabilità . Una volta collegati gli archi locali nel grafo, si esegue il rewiring andando a collegare un generico nodo ad un generico nodo non connesso ad con probabilità Dove è un parametro chiamato esponente di clustering. Se , allora il modello stimolerà le connessioni a più alta distanza, chiamate long range edge, mentre per gli archi saranno più frequentemente su nodi vicini. Sia il numero di dimensioni del lattice, modificando si ottengono diversi gradi di navigabilità:
- Per i link sono scelti in maniera uniforme su tutta la rete (mod. Watts-Strogatz);
- Per si tende a scegliere archi con nodi vicini
- La ricerca decentralizzata trova rapidamente un target nelle vicinanze, ma lo raggiunge lentamente se è lontano.
- Per si tende a scegliere molti archi con nodi lontani
- La ricerca decentralizzata si avvicina rapidamente all'area del target, ma poi rallenta fino a raggiungere il target.
- Per si ottiene una navigabilità ottimale per la rete.
Si osservi il plot che mostra nell'ascisse l'esponente di clustering e nelle ordinate il tempo di navigazione. Tale plot rispecchia quanto detto per un lattice bidimensionale.
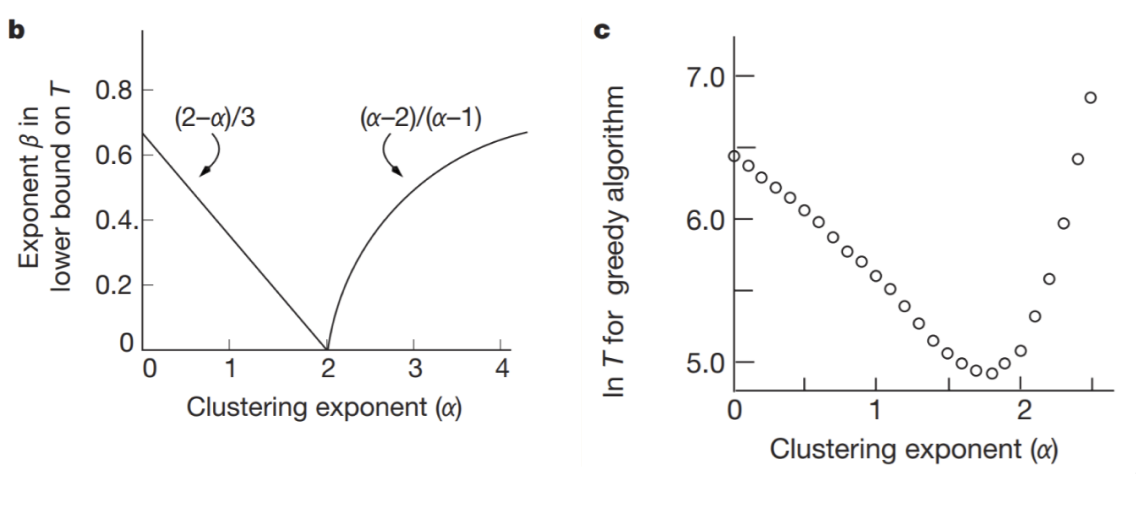
Teorema
Sia la distanza tra due nodi e di una griglia bidimensionale () di nodi. Se tra due vertici e viene aggiunto un arco remoto con probabilità con allora esiste un algoritmo di routing decentralizzato ed una costante indipendente da tali che, quando (distanza massima affinché un nodo sia considerato "vicino") e (numero di archi long range per nodo) il numero di passi impiegati da per trasmettere un messaggio tra una coppia qualsiasi di nodi è al più .
Alcune referenze per il modello di Kleinberg:
- https://www.nature.com/articles/35022643.pdf
- https://chih-ling-hsu.github.io/2020/05/15/kleinberg
Confrontiamo infine i modelli visto sino ad ora rispetto alla navigabilità:
| Kleinberg | Watts-Strogatz | Erdos-Renyi | |
|---|---|---|---|
| Navigabile? | Yes | No | No |
| T | |||
| Search time |
2.2.2 Configuration model
Il configuration model è un modello in grado di generare un rete con una sequenza di gradi fissata . La procedura con cui si crea una rete attraverso il configuration model consiste nel generare, per ogni nodo, il rispettivo grado. I nodi vengono accoppiati casualmente. È utile come modello nullo, per confrontare una rete reale con una rete che la ha stessa frequenza di gradi, quindi la stessa distribuzione dei gradi .
2.2.1 Distribuzione power-law
Nel modello Watts-Strogatz la distribuzione dei gradi dei nodi risulta essere una distribuzione simile alla Poisson, analogo nel modello di Erdos-Renyi. Come abbiamo visto, nelle reti reali la distribuzione dei gradi non è affatto simile alla distribuzione di Poisson. Piuttosto, è ben approssimata da una distribuzione chiamata power-law.
Una distribuzione è una power-law se: Dove il parametro è detto esponente di grado. Si può dimostrare che sopra un certo valore , la distribuzione power law è sempre più alta della distribuzione esponenziale, quindi Nelle reti reali si osserva generalmente . Vediamo a confronto la distribuzione power-law e quella di Poisson. Si osservi che, in scala log-log (b) la distribuzione power-law assume la forma di una retta di pendenza .
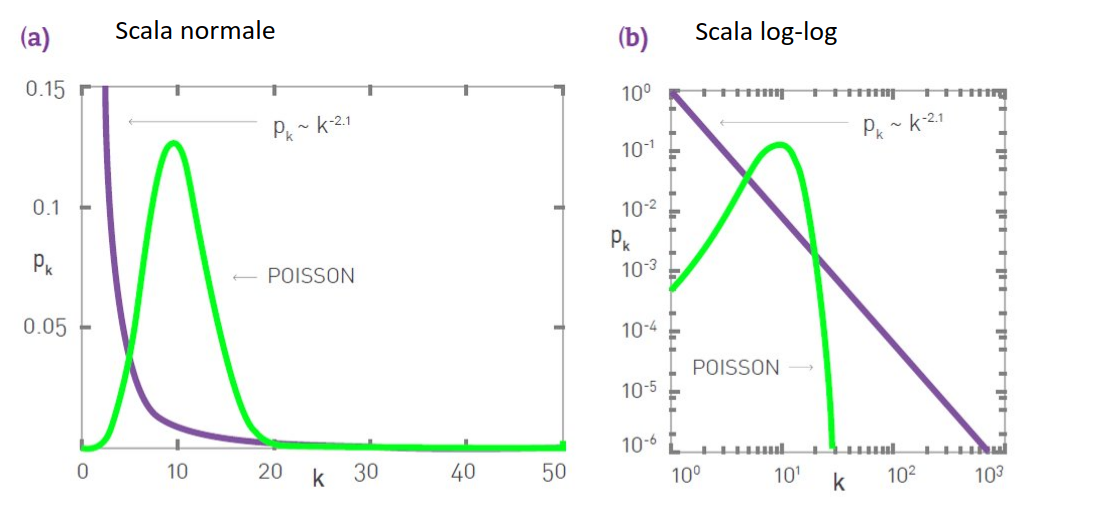
Studiare la legge di potenza in una rete reale
Supponiamo di avere a disposizione una rete reale che segue una legge di potenza Siamo interessati a conoscere la costante di normalizzazione e l'esponente di grado . Essendo una distribuzione di probabilità, l'area sotto la curva varrà 1: Dove è un numero stimabile dai dati reali, dopo il quale la distribuzione segue la legge di potenza. Risolvendo l'equazione rispetto a otteniamo che Quindi sostituendo la nella distribuzione dei gradi otteniamo Il valore atteso di tale distribuzione risulta essere: Se allora il valore atteso assume un valore negativo. Tuttavia non è possibile avere un grado negativo, per cui il valore atteso diverge a . Per anche la varianza diverge a .
Per stimare l'esponente di grado è possibile utilizzare la Maximum Likelihood: Vogliamo trovare che massimizza , per cui settiamo e risolviamo l'equazione. Ne segue che:
2.2.2 Rete scale-free
Le reti la cui distribuzione dei gradi segue una distribuzione power-law sono dette reti scale-free, o invarianti per scala. Ciò implica che nelle reti scale-free vi è una piccola porzione di nodi che hanno un grado elevato ed una elevata porzione di nodi, che copre quasi tutta la rete, con basso grado. I nodi di elevato grado vengono chiamati anche hub.
Una rete scale-free è quindi caratterizzata dalla presenza di un certo numero di hub, che risultano essere praticamente assenti nelle reti random o small-world. Il comportamento scale-free delle reti reali riflette perfettamente ciò che accade in tantissimi ambiti della società attuale (economia, rapporti sociali, etc.) ed è ben riassunto dalla regola di Pareto, o regola 80/20.
Il termine "scale-free" si riferisce all'assenza di una scala, ovvero un valore di riferimento per stabilire il grado di un nodo qualsiasi della rete. In una rete random in cui la distribuzione dei gradi è di Poisson, la media corrisponde al picco della curva e i gradi dei rimanenti nodi si discostano poco dalla media (varianza finita e bassa): in tal caso la media rappresenta il valore di scala.
In una rete scale-free, in cui la distribuzione dei gradi è power-law, la varianza della distribuzione diverge per molto grande. Ciò implica che se scegliamo in maniera casuale un nodo, non possiamo dire nulla sul suo grado: può essere estremamente piccolo o estremamente grande. Non possiamo quindi indicare un ordine di grandezza o una scala al grado di un nodo.
La presenza di hub in una rete scale-free ha una conseguenza importante: rende in generale la rete più robusta ad attacchi o situazioni per cui uno o più collegamenti nella rete vengono meno. Se in una rete random un nodo qualsiasi viene giù o un collegamento si interrompe, l'intera rete potrebbe essere compromessa. I punti sensibili di una rete scale-free sono gli hub, che collegano la maggior parte dei nodi.
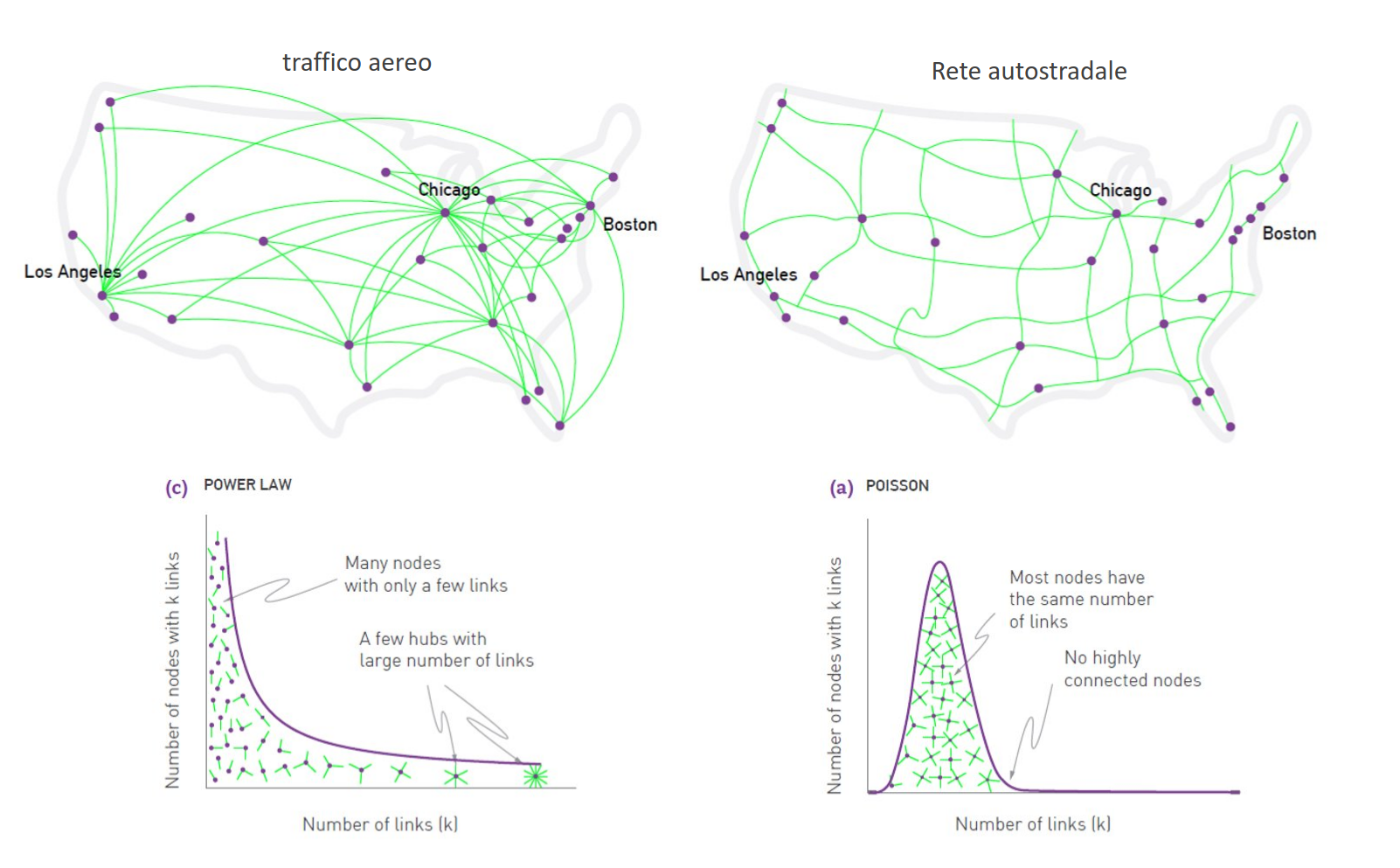
Proprietà ultra small-world
La presenza degli hub in una rete scale-free ha un'altra importante conseguenza: riduce la distanza media tra i nodi. Per valori dell'esponente di grado si parla di ultra small-world. In questo scenario la distanza media tra i nodi è più piccola della distanza media osservata nella rete random. Per la rete è small-world ed ha proprietà che la rendono molto simile ad una rete random. Nel caso per che tende ad infinito sia la media che la varianza divergono, ciò implica che non possono esistere reti grandi con . Per le reti ultra small-world si ha:
2.2.3 Perché le reti reali sono scale-free?
Come abbiamo visto, molte reti reali sono scale-free, indipendentemente dalla loro natura e dalla loro dimensione. Perché sistemi così diversi convergono verso architetture simili tra loro? Quali sono i meccanismi che fanno emergere la proprietà scale-free? Dunque bisogna investigare sul modo in cui le reti reali si evolvono nel tempo. Vediamo due caratteristiche principali delle reti reali.
Crescita della rete
Nelle reti reali il numero di nodi cresce continuamente grazie all'aggiunta di nuovi nodi anziché essere fissato a priori come nei modelli random visti in precedenza.
Preferential attachment
Nelle reti reali un nuovo nodo che entra nella rete tende a legarsi ai nodi più connessi, cioè a quelli più importanti, mentre nella rete random i partner di un nodo sono scelti in modo random. Basti pensare ai followers di Twitter o alle citazioni negli articoli.
2.3 Modello di Barabasi-Albert
La crescita ed il preferential attachment sono proprio le due proprietà cardine del modello di Barabasi-Albert o modello scale-free, proposto nel '99 da Albert-Laszlo Barabasi e Reka Albert. La procedura di generazione del grafo è la seguente:
- Crea una rete random iniziale con nodi, in cui ogni nodo abbia grado almeno pari a 1.
- Aggiungi un nuovo nodo alla rete e collegalo a nodi esistenti nella rete.
- La probabilità che un nuovo nodo si colleghi ad un nodo esistente di grado è:
- Ripeti il passo 2 sino a quando non si ottiene il numero desiderato di archi.
Il passo 2 realizza il preferential attachment in quanto è direttamente proporzionale al grado . Il preferential attachment favorisce la formazione degli hub. Un nodo con alto grado ha più probabilità di un nodo con basso grado di stabilire nuove connessioni e diventare sempre più importante e centrale nella rete. Questo fenomeno è sintetizzato dall'espressione "rich gets richer". Attraverso il modello Barabasi-Albert si possono quindi creare reti scale-free.
2.3.1 Variante del modello
Supponiamo di introdurre una variabile distribuita uniformemente. Allora possiamo modificare il nostro modello che sfrutta il preferential attachment come segue:
- Con probabilità si collega ad un nodo random
- Con probabilità si collega utilizzando il preferential attachment
Se , allora il modello ricade nel modello standard di Barabasi-Albert. Da tale costruzione del modello, ne deriva che
Graph matching
1. Introduzione
1.1 Isomorfismo tra grafi
L'isomorfismo tra grafi (o graph matching) consiste nel verificare se due grafi sono "uguali" tra loro, ovvero hanno una corrispondenza (o matching). Formalmente, due grafi e si dicono isomorfi se: Ovvero se ad ogni arco tra due nodi e appartenenti a , esiste un arco tra i nodi ed appartenenti al grafo . Tale funzione è biiettiva e prende il nome di mapping. In altri termini, è possibile ri-etichettare i nodi di come nodi di , mantenendo la relazione tra gli archi di e quelli corrispondenti di .
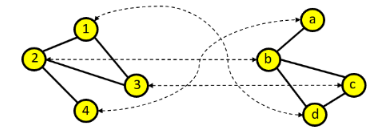
1.2 Isomorfismo tra sottografi
L'isomorfismo tra sottografi (o subgraph matching) consiste nel verificare se un grafo (detto grafo query) è contenuto in (quindi è sottografo di) un altro grafo più grande (detto grafo target). Formalmente, un grafo è un sottografo isomorfo di un grafo se La funzione prende ancora il nome di mapping e, dal momento in cui è solamente iniettiva, non è necessario che tutti i nodi di siano mappati. Al contrario, tutti i nodi del sottografo query lo saranno.
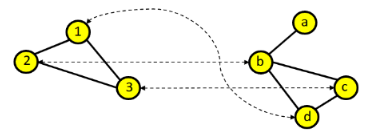
1.3 Matching multipli ed automorfismi
La soluzione del graph matching (o subgraph matching) non è univoca, in generale possono esistere varie funzioni di mapping .
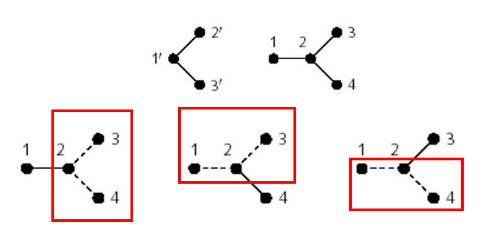
L'isomorfismo tra un grafo e se stesso è detto automorfismo di . Un grafo può avere più automorfismi:
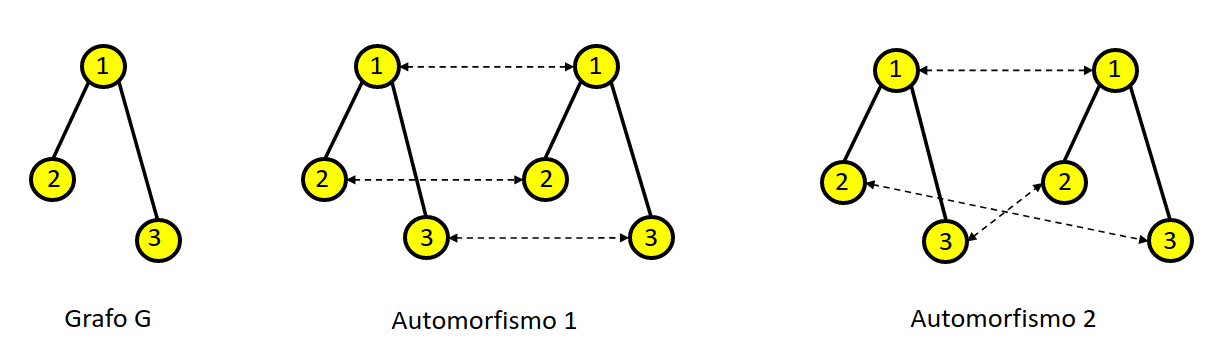
1.4 Complessità del matching
Il graph matching è un problema NP-hard, ma non si sa se sia NP-completo. Invece, il problema del subgraph matching è NP-completo, per cui se si trovasse una soluzione il cui tempo è polinomiale, allora si potrebbe usarla per risolvere ogni problema NP (si rimanda ai casi di complessità P e NP).
1.5 Algoritmi sviluppati
Per quanto concerne il graph matching, alcuni dei più famosi algoritmi sviluppati sono: Bliss, Saucy, Conauto, Nauty (ora Traces). Questi tool si basano sulla trasformazione dei grafi in una rappresentazione standard, chiamata forma canonica, in modo tale che due grafi isomorfi abbiano la stessa forma canonica. L'efficienza di tali algoritmi è legata all'efficienza della trasformazione dei grafi in forma canonica. In generale, non esiste un algoritmo migliore. A seconda del tipo di rete un algoritmo può essere migliore di altri. Su grafi reali, Nauty è sinora l'algoritmo migliore. Alcuni di questi algoritmi contengono una serie di utilità interessanti sui grafi, ad esempio la possibilità di generare tutti i possibili grafi connessi con nodi. Per quanto riguarda il subgraph matching possiamo riferirci a: Algoritmo di Ullmann ('76), algoritmo di Von Scholley ('84), VFlib, LAD, Focus-Search, RI.
2. Algoritmi di subgraph matching
Tutti gli algoritmi di subgraph matching hanno una procedura simile: esplorano un particolare albero di ricerca. Ipotizziamo che sia il grafo query e sia il grafo target:
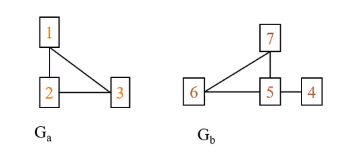
La root dell'albero di ricerca indica che nessun mapping è stato effettuato. Partiamo da un nodo qualsiasi di , ad esempio 1: possiamo mappare il nodo 1 con uno qualsiasi dei quattro nodi di . Per cui la root avrà 4 rami uscenti, ognuno di essi considera un diverso mapping del primo nodo. Per ognuno di questi nodi viene scelto un secondo nodo che non sia ancora mappato e vengono fatte le stesse considerazioni. L'albero si estende sino a che per ogni ramo tutti i nodi di siano stati mappati. Ogni cammino che porta dalla radice ad una foglia indica una diversa mappatura, non necessariamente valida (nell'esempio solo le soluzioni evidenziate con un rettangolo sono valide).
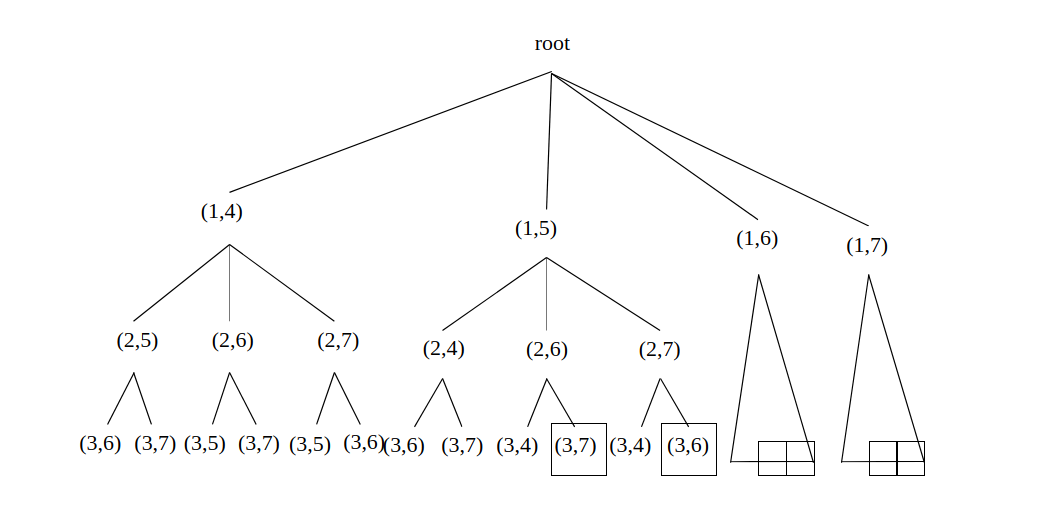
2.1 Algoritmo brute-force
La soluzione bruteforce è una soluzione naive che consiste nel provare tutti i possibili cammini, per cui viene generato ed esplorato l'intero albero di ricerca, alla ricerca di mappature valide. L'algoritmo termina quando tutti i nodi del grafo query sono stati mappati con successo o tutte le alternative per fare matching con un nodo target sono state esplorate. Se un grafo ha nodi, vi saranno possibili match, per cui tale soluzione è particolarmente inefficiente.
2.2 Strategie di ricerca
Occorrono delle strategie che aiutino a velocizzare la computazione. Vedremo in particolare due strategie: la look-ahead ed il backtracking.
2.2.1 Strategia del look-ahead
La strategia del look-ahead (guarda avanti) consiste nel predire anticipatamente che il matching parziale prodotto da un cammino parziale non porterà ad una soluzione valida finale.
2.2.2 Strategia del backtracking
La strategia del backtracking consiste nell'abbandonare soluzioni parziali nel momento in cui ci accorgiamo che non portano a soluzioni finali.
2.3 Algoritmo di Ullmann
L'algoritmo di Ullmann utilizza il grado del nodo per fare look-ahead e backtracking e filtrare lo spazio di ricerca delle possibili soluzioni. L'idea principale, come visto in precedenza, è che se il nodo del grafo query ha un grado maggiore del nodo corrispondente nel grafo target, allora banalmente non è possibile arrivare ad una soluzione, per cui viene effettuato il pruning.
Supponiamo di dover fare graph matching tra i grafi in figura. Osservando il cammino più a sinistra (leftmost) notiamo che dopo aver mappato il nodo 2 con il nodo , il primo ramo sottostante suggerisce di mappare il nodo 3 con il nodo . Tuttavia, basta osservare che il nodo 3 ha un grado maggiore (3) del nodo c (2), quindi il cammino non potrà portare ad una soluzione.
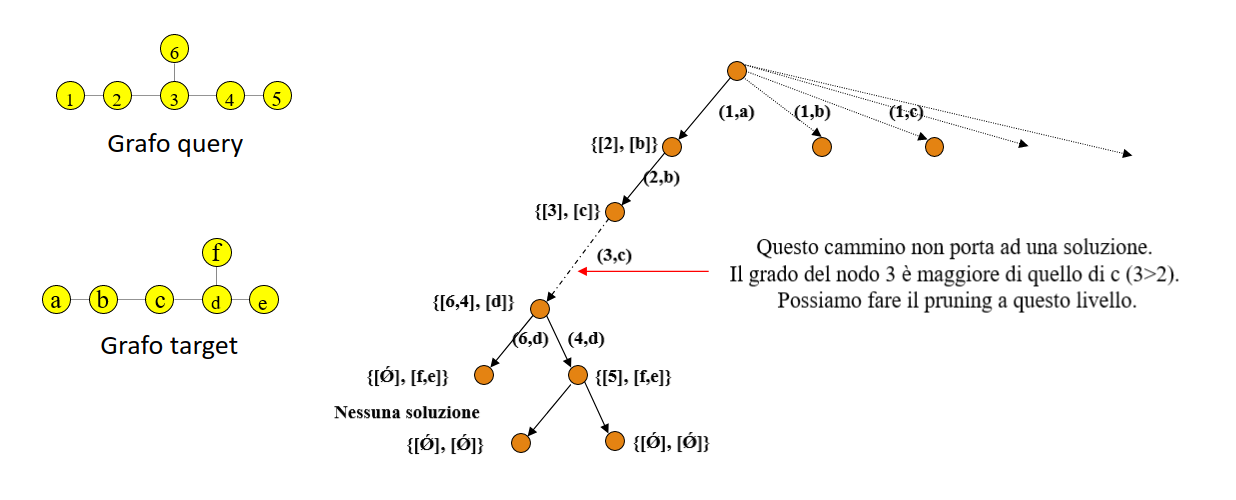
2.4 algoritmo VF
L'algoritmo VF (Vento-Foggia) si basa sul concetto di State Space Representation (SSR).
Il processo di matching è visto come una successione di stati. Ad ogni stato sono associati vari insiemi:
- L'insieme , detto mapping parziale, rappresenta l'insieme di coppie di nodi già mappate
- L'insieme rappresenta l'insieme di coppie candidate ad essere aggiunte ad .
L'aggiunta di una coppia di nodi mappati in provoca la transizione ad un nuovo stato. La coppia può essere aggiunta se e solo se soddisfa delle regole di fattibilità.
PROCEDURE match (s)
IF M(s) contiene tutti i nodi del grafo query
THEN OUTPUT M(s)
ELSE
calcola l'insieme P(s)
FOREACH p in P(s)
IF p soddisfa tutte le regole di fattibilità THEN
aggiungi p a M(s)
calcola lo stato s' dopo l'aggiunta
OUTPUT CALL(s')
END IF
END FOREACH
END IF
END PROCEDURE
2.4.1 Definizione degli insiemi
L'algoritmo VF definisce 6 insiemi di nodi:
- insieme di nodi del grafo query mappati, quindi in M(s)
- insieme di nodi del grafo target mappati, quindi in M(s)
- insieme di nodi del grafo query adiacenti ai nodi in
- insieme di nodi del grafo target adiacenti ai nodi in
- insieme dei nodi del grafo query rimanenti
- insieme dei nodi del grafo target rimanenti
L'insieme è così definito:
P(s) = { (u,v) \mid u \in T_1(s) \and v \in T_2(s) }
Le regole di fattibilità sono differenti a seconda si tratti di grafi diretti o grafi indiretti.
2.4.2 Regole di fattibilità - grafi indiretti
Una coppia viene aggiunta ad se e solo se soddisfa le seguenti tre regole.
Consistenza del nuovo stato
Per ogni nodo connesso ad , il corrispondente nodo è connesso ad .
Regola del look-ahead ad un livello
Il numero di nodi in connessi ad è minore o uguale al numero di nodi in connessi ad .
Regola del look-ahead a due livelli
Il numero di nodi in connessi ad è minore o uguale al numero di nodi in connessi ad .
2.4.3 Regole di fattibilità - grafi diretti
Una coppia viene aggiunta ad se e solo se soddisfa le seguenti cinque regole.
Consistenza del nuovo stato
Per ogni nodo predecessore di , il corrispondente nodo è predecessore di .
Per ogni nodo successore di , il corrispondente nodo è successore di .
Regola del look-ahead ad un livello
Il numero di nodi in adiacenti ad è minore o uguale al numero di nodi in adiacenti ad .
Il numero di nodi in a cui è adiacente è minore o uguale al numero di nodi in a cui è adiacente.
Regola del look-ahead a due livelli
Il numero di nodi in connessi a è minore o uguale al numero di nodi in connessi ad .
Osservazione: se si vuole cercare l'isomorfismo tra grafi anziché sottografi è possibile sostituire il minore o uguale con l'uguale.
2.4.4 Complessità dell'algoritmo
Supponiamo che ambo i grafi abbiano nodi. Nel caso pessimo ogni nodo ha adiacenti (grafo regolare). Il primo passo di esplorazione ha scelte. Nel caso migliore ad ogni passo il primo nodo soddisfa le regole, per cui la complessità finale è . Nel caso pessimo, per ogni scelta bisogna esplorare tutte le possibili permutazioni del grafo target, quindi la complessità sarà .
Se consideriamo le informazioni relative allo stato, l'algoritmo memorizza per ogni nodo una quantità costante di informazioni, ovvero il mapping e l'appartenenza ai vari insiemi. Al più stati (e le informazioni associate) risiederanno simultaneamente in memoria in un certo momento della computazione.
2.4.5 Algoritmo VF2
Una versione successiva dell'algoritmo, chiamata VF2, ottimizza lo spazio utilizzato sino ad ottenere una complessità spaziale pari a . L'idea è quella di usare strutture dati globali, condivise tra i vari stati, ed evitare la memorizzazione di diverse copie di vettori delle informazioni sui nodi per ciascuno stato.
Introduciamo le strutture e rispettivamente di lunghezza pari al numeri di nodi dei rispettivi grafi. Le strutture sono tali che , simmetricamente per . Si introducono dei nuovi insiemi che indicano il tempo in cui un nodo entra a far parte di o di rispettivamente. Tali strutture servono a gestire meglio le strutture dati globali.
In questo modo si tiene traccia contemporaneamente dell'appartenenza del nodo agli insiemi terminali e dello stato corrispondente della computazione. Quando si fa backtracking, si ripristina il precedente valore di questi vettori.
2.5 Algoritmo RI
Le regole di fattibilità (o di pruning in generale) possono ridurre molto lo spazio di ricerca ma sono costose da implementare. In realtà, l'aspetto più importante è l'ordine in cui i nodi della query vengono processati dall'albero di ricerca. Un ordinamento efficace dei nodi può velocizzare molto il matching, anche in presenza di regole di pruning più leggere. Quest'ordine può essere calcolato indipendentemente dal grafo target, nel caso dello static ordering, oppure sulla base del grafo target, nel caso del dynamic ordering. L'algoritmo RI si basa su uno static ordering dei nodi della query.
2.5.1 procedura dell'algoritmo
L'algoritmo prevede un preprocessing in cui applica lo static ordering, ovvero ordina i nodi del grafo della query in modo da massimizzare la probabilità che un cammino parziale non valido nell'albero di ricerca venga tagliato prima possibile.
Dopo il preprocessing si provvede ad esplorare lo spazio di ricerca seguendo l'ordinamento stabilito. Si mappano i nodi del grafo query sui nodi del grafo target rispettando la regola del grado dettata dall'algoritmo di Ullmann, quando viene trovato un match completo, si memorizza l'occorrenza trovata. Si procede iterando il passo precedente sino a che l'intero spazio di ricerca non è stato esplorato.
2.5.2 Ordinamento statico
Dato un grafo query con nodi, l'obiettivo dell'ordinamento statico è quello di costruire una sequenza ordinata di nodi , sequenza che verrà rispettata durante l'esplorazione dell'albero di ricerca.
Per costruire tale sequenza si procede ad iterazioni:
- Al tempo 0 l'insieme è vuoto.
- Al tempo 1 viene inserito in il nodo con il grado massimo.
- Al generico tempo viene inserito il nodo con il più alto numero di vicini in .
Quindi nodi con alto grado e che hanno un elevato numero di connessioni con nodi già presenti nell'ordinamento vengono inseriti prima nella sequenza ordinata. In generale, ad ogni iterazione si calcola un punteggio per ogni nodo.
Sia la sequenza ordinata parziale. Il punteggio di un nodo candidato è definito sulla base di 3 insiemi:
- L'insieme di nodi in adiacenti a .
- L'insieme di nodi in adiacenti ad almeno un nodo che non appartiene ad e che è connesso a .
- L'insieme di nodi connessi a che non stanno in e non sono nemmeno connessi a nodi di .
Il successivo nodo da inserire nell'ordinamento è quello che ha:
-
- Massimo valore di
-
- In caso di parità in 1, massimo valore di
-
- In caso di parità in 2, massimo valore di
-
- In caso di parità in 3, il nodo è scelto arbitrariamente.
2.5.3 Regole di pruning
Una coppia è accettata se e solo se:
- Né né sono già stati mappati nella soluzione parziale
- I due nodi hanno la stessa etichetta (in un grafo etichettato)
- Il grado di sia maggiore o uguale al grado di (Algoritmo di Ullman).
3. Graph matching in un database
Dato un database di grafi ed un grafo query , il problema del graph matching in un database consiste nel trovare tutti i grafi che contengono come sottografo (o come grafo).
3.1 Indexing
La soluzione banale consiste nell'applicare un algoritmo di graph matching (come il RI) su ciascun grafo del database, ma ciò richiederebbe troppo tempo. Per ottenere tempi di risposta ragionevoli, occorre indicizzare (indexing) in qualche modo i grafi del database ed il grafo query. L'indicizzazione può essere effettuata offline una volta sola per i grafi del database. Vedremo due tipi di indicizzazione, a seconda se ci si basa o meno sulle feature.
3.1.1 Indicizzazione basata su feature
Si rappresenta il grafo mediante un insieme di attributi (o feature) e prima di applicare qualsiasi algoritmo di matching si filtrano tutti i grafi del database che non contengono tutte le feature del grafo query. Esempi di algoritmi sono gIndex, TreePi, GraphFind. Le feature estraibili dai grafi sono: piccoli sottografi, alberi, cammini. Gli ultimi due sono più semplici da estrarre rispetto ad i sottografi.
Ipotizziamo di indicizzare i grafi per cammini di lunghezza 2 e di dover confrontare i due grafi sottostanti. Il grafo query ha molti più cammini di lunghezza 2 rispetto al grafo proveniente dalla base di dati. Inoltre, essendo etichettati, è possibile effettuare un confronto preciso dei protagonisti del cammino. Il grafo del database verrà scartato.
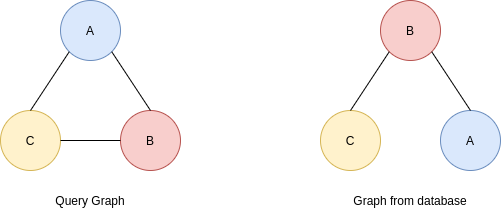
3.1.2 Indicizzazione non basata su feature
I grafi del database vengono memorizzati solitamente in un albero (B-tree, R-tree). Tali sistemi sono più adatti per frequenti aggiornamenti del database. Alcuni algoritmi sono Ctree o GCoding.
3.2 Schema base
Lo schema base di graph matching in un database di grafi consiste in 3 passi: preprocessing, filtering e matching.
- Nella fase di preprocessing vengono estratte le feature da ogni grafo del database (cammini, alberi, sottografi). Le feature vengono memorizzate utilizzando l'indicizzazione inversa.
- Nella fase di filtering si estraggono le features dalla query e vengono filtrati dal database solo i grafi che contengono tutte le feature del nodo query.
- Nella fase di matching viene applicato un algoritmo di graph matching ad ogni grafo del database filtrato per verificare se contiene o meno il grafo query.
3.2.1 Indicizzazione inversa
L'indicizzazione inversa consiste nell'indicizzare le feature estratte anziché i dati. Ipotizziamo di avere un insieme di feature , ad ognuna di esse verranno associati tutti i grafi che la contengono e quante volte la contengono.
3.3 Algoritmo SING
L'algoritmo SING, acronimo per subgraph search in non-homogeneous graphs, si bassa sull'idea che, per migliorare l'efficacia dell'indice, è possibile associare ad ogni feature non solo il numero di volte in cui esso è presente nel grafo, ma anche il nodo da cui parte. Consideriamo il seguente esempio:
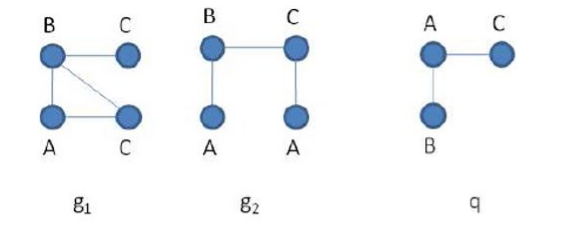
I cammini ed sono presenti in ambo i grafi e , tuttavia, solo contiene la query. Ciò è legato al fatto che entrambi i cammini partono dallo stesso nodo in , ma da nodi diversi in .
3.3.1 Indicizzazione in SING
L'algoritmo SING prevede due tipi di indici: uno globale per tutti i grafi ed uno locale per ciascuno dei grafi. Nell'indice inverso globale ad ogni feature costituita da cammini di lunghezza al più viene associata la lista dei grafi del database che la contengono ed il relativo conteggio.
Ad ogni grafo del database viene associato un indice inverso locale che contiene, per ogni feature presente in , un vettore binario dove l'-esimo elemento è 1 se esiste un occorrenza di che parte dal nodo , 0 altrimenti.
3.3.2 Preprocessing della query
Filtering 1: Per ogni feature del grafo query, viene selezionato l'insieme dei grafi in cui occorre un numero di volte maggiore o uguale al numero di occorrenze nel grafo query. Viene quindi calcolata l'intersezione di tutti questi insiemi.
Filtering 2: Per ogni grafo , viene utilizzato l'indice locale di per calcolare gli insiemi di nodi compatibili (cioé mappabili) con i nodi della query. Vengono scartati i grafi per cui almeno un nodo della query non ha nodi compatibili corrispondenti.
Quando due nodi sono detti compatibili? Supponiamo di dover controllare la compatibilità tra un nodo del grafo query ed un nodo del grafo del database. Possiamo dire che è compatibile con se tutte le feature che partono da nel grafo query partono da nel grafo . Se è l'insieme di queste feature che partono da , allora è sufficiente calcolare nell'indice locale del grafo un AND logico tra i vettori binari associati alle feature di .
Matching: Per ogni grafo candidato che ha superato le due fasi di filtering, viene applicato un algoritmo di matching per verificare se contiene o meno il grafo query.
Graph Mining
1. Introduzione
Similmente al modello transazionale ritrovato nel Market Basket Analysis, dove lo scopo era quello di trovare gli itemset frequenti in un database di transazioni, il problema del frequent subgraph mining (FSM) consiste nell'identificare tutti i sottografi che occorrono frequentemente in un database di grafi.
1.1 Supporto, soglia e frequenza
Tipicamente si conta il numero di grafi del database che contengono il sottografo, tale numero prende il nome di supporto. Se il supporto del sottografo è maggiore o uguale ad una soglia minima , allora il sottografo è detto frequente. L'output di un algoritmo di FSM è l'insieme di tutti i sottografi frequenti, con il loro supporto.
Vediamo un esempio con soglia :
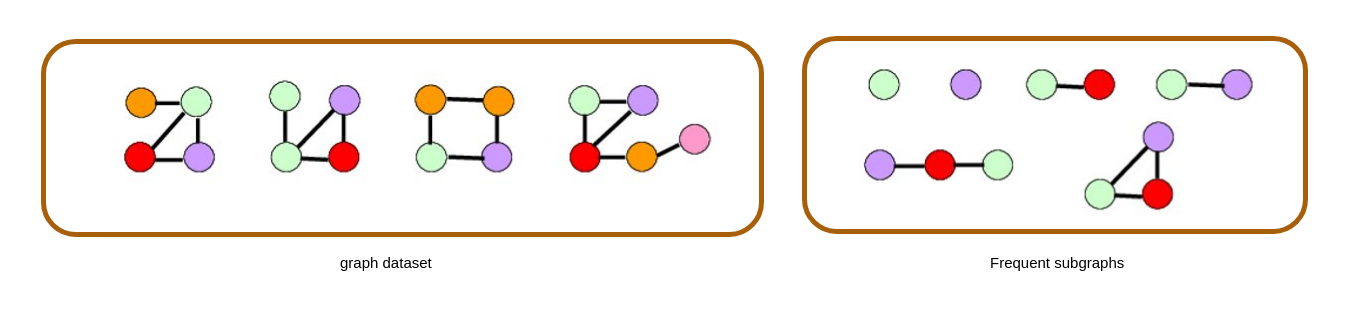
Piuttosto che fare riferimento al supporto, che è un conteggio assoluto, spesso si utilizza la frequenza, che è invece un conteggio relativo. La frequenza di un sottografo in un database è il rapporto tra il supporto ed il numero di grafi nel database. La soglia minima in questo caso sarà espressa come una percentuale. Un sottografo è frequente se è presente in almeno % grafi del database.
1.3 Regola Apriori
Come nel caso del Market Basket Analysis, anche nel Frequent Subgraph Mining è possibile sfruttare la regola apriori per filtrare i candidati e ottimizzare la ricerca dei sottografi frequenti. La regola apriori è la seguente:
Il supporto di un sottografo in un database di grafi non può essere maggiore del supporto dei sottografi che contiene.
In altre parole, se un sottografo non è frequente, allora nessun sottografo che contiene è frequente. Ciò pone la base per lo schema generale di un algoritmo di Frequent Subgraph Mining.
1.4 Schema generale
Osserviamo adesso lo schema generale di un algoritmo di Frequent Subgraph Mining. Sia l'insieme finale di sottografi frequenti e sia la soglia imposta, il primo step è il seguente:
- Cercare singolarmente tutti i nodi frequenti nel database ed insierirli in .
Nell'insieme abbiamo adesso grafi formati da un solo nodo e frequenti.
- Per ogni elemento in generiamo tutti i possibili grafi con 2 nodi, candidati ad essere frequenti.
- Tra i sottografi generati, eliminiamo i duplicati e verifichiamo la regola apriori.
- Scartiamo tutti i grafi in cui è presente un sottoinsieme non frequente.
- Calcoliamo il supporto di ogni grafo candidato e, se risulta essere frequente, aggiungiamolo ad .
Lo step è generalizzabile per , ed ogni sotto-passo ha un nome specifico:
- Candidate generation: a partire dall'insieme dei sottografi frequenti con nodi, costruire l'insieme dei sottografi candidati con nodi.
- Pruning: eliminare i sottografi ridondanti e verificare la regola Apriori, ovvero si scartano tutti i candidati che contengono almeno un sottografo con nodi non frequente.
- Counting: calcola il supporto di ogni grafo candidato e l'insieme dei sottografi frequenti con nodi. Aggiungi questi ultimi all'insieme finale .
Quando al generico passo si verifica che l'insieme di sottografi frequenti con nodi è vuoto, la computazione termina, ovvero non ci sono ulteriori sottografi frequenti. Quindi viene restituito l'insieme in output.
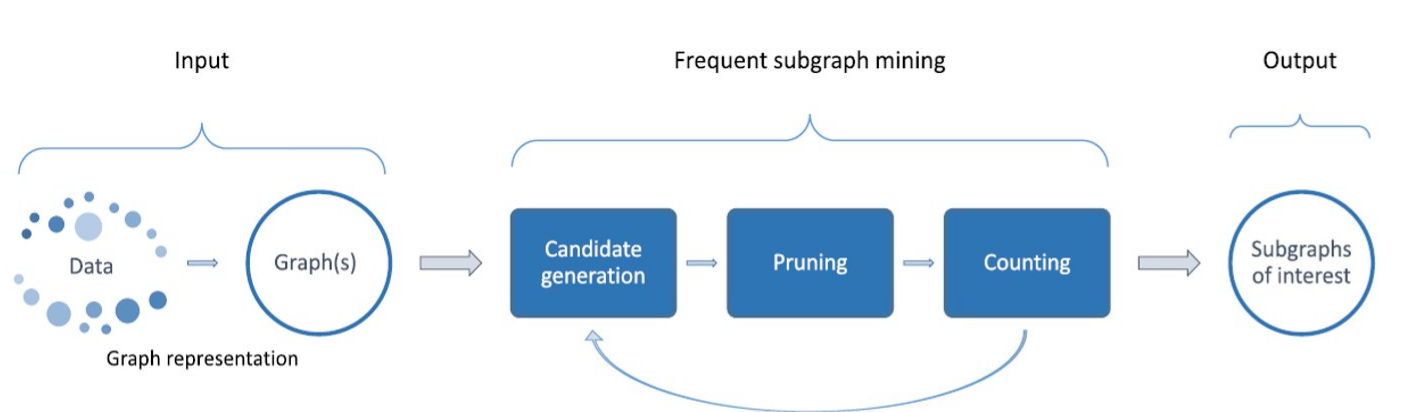
1.5 Approcci BFS e DFS
L'approccio descritto in precedenza è basato su una strategia in ampiezza, ovvero BFS (Breadth-first Search): prima di generare i sottografi candidati con nodi, si calcolano tutti i sottografi frequenti con nodi.
Esiste anche un approccio alternativo che utilizza la strategia DFS (Depth-first search): si calcola il supporto di un sottografo candidato con nodi e, se è frequente, si estende. Quindi si controlla il supporto del sottografo esteso e così via. L'approccio DFS richiede meno memoria, ma risulta meno efficace nel pruning.
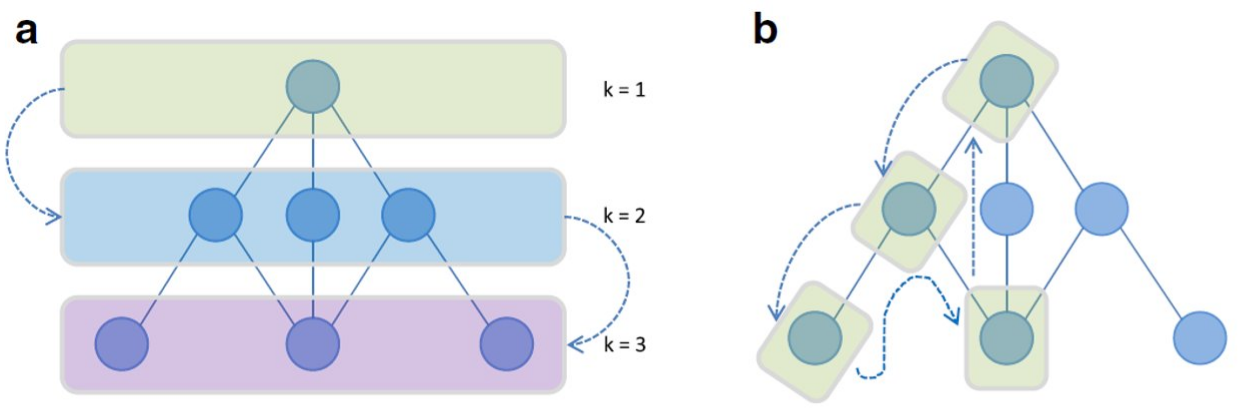
1.6 Generazione dei candidati
1.6.1 Generazione Join-based
Un sottografo candidato con nodi è ottenuto dall'unione di due sottografi con nodi frequenti. L'unione è possibile se e solo se i due sottografi hanno almeno un sottografo con nodi in comune, chiamato core graph. Nell'esempio osserviamo due possibili risultati: in uno dei due viene inserito un arco tra i due nodi esterni al core, mentre nell'altro no.
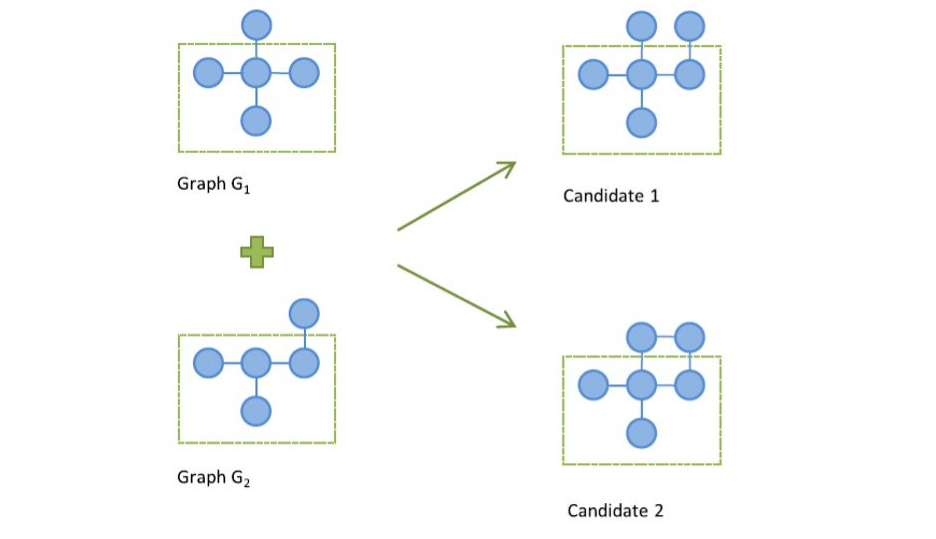
La generazione può essere fatta basandosi sugli archi. In tal caso, si aggiunge al grafo frequente un arco di un altro grafo frequente con lo stesso core. Eventualmente è possibile aggiungere, oltre l'arco, anche un nodo. Vediamo nell'esempio in figura che mentre il candidato 2 inserisce solo l'arco, il candidato 1 include anche il nodo.
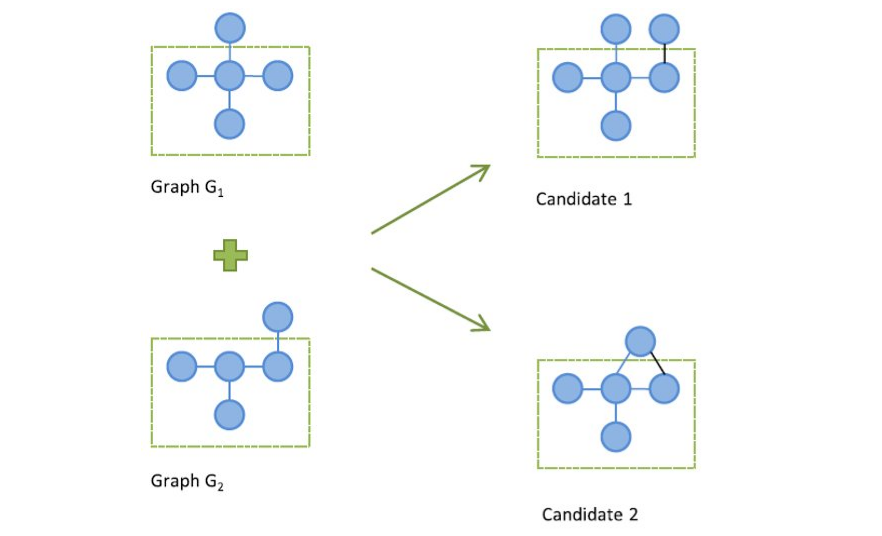
Una join tra due grafi può produrre più candidati per i seguenti motivi:
- I due sottografi hanno più di un core-graph in comune;
- Un core-graph può avere più di un automorfismo;
Inoltre lo stesso candidato può essere generato a partire da join diverse, per cui è necessario un successivo passo di pruning che elimini i candidati duplicati.
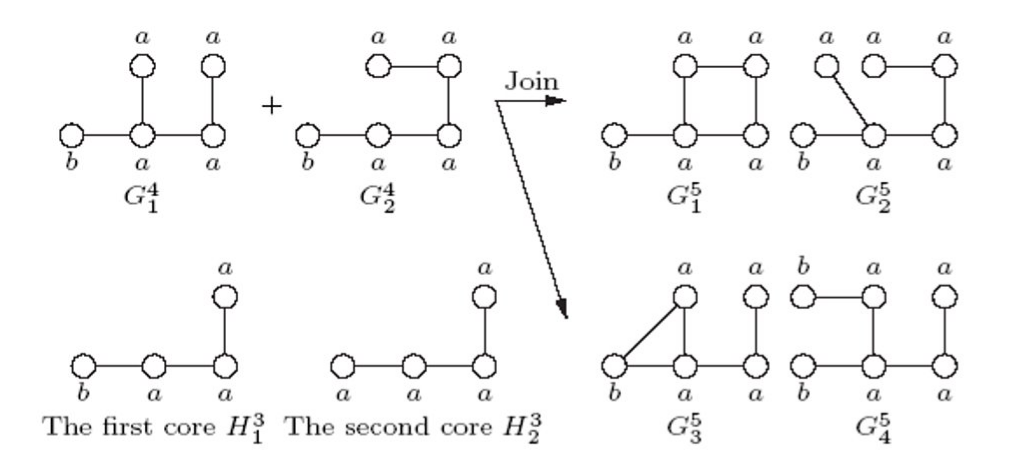
1.6.2 Generazione Extend-based
Un sottografo candidato con nodi è generato estendendo un sottografo frequente con nodi mediante l'aggiunta di un solo nodo.
L'aggiunta può essere effettuata in vari modi. Una tecnica per evitare la generazione di sottografi candidati ridondanti consiste nell'effettuare l'estensione seguendo il cammino right-most di una visita DFS effettuata sul grafo: il nodo viene aggiunto solo a partire da nodi che risiedono nel cammino più a destra nell'albero di visita DFS del grafo da estendere. Anche tale estensione può essere fatta aggiungendo un arco anziché un nodo. Vediamo un esempio:
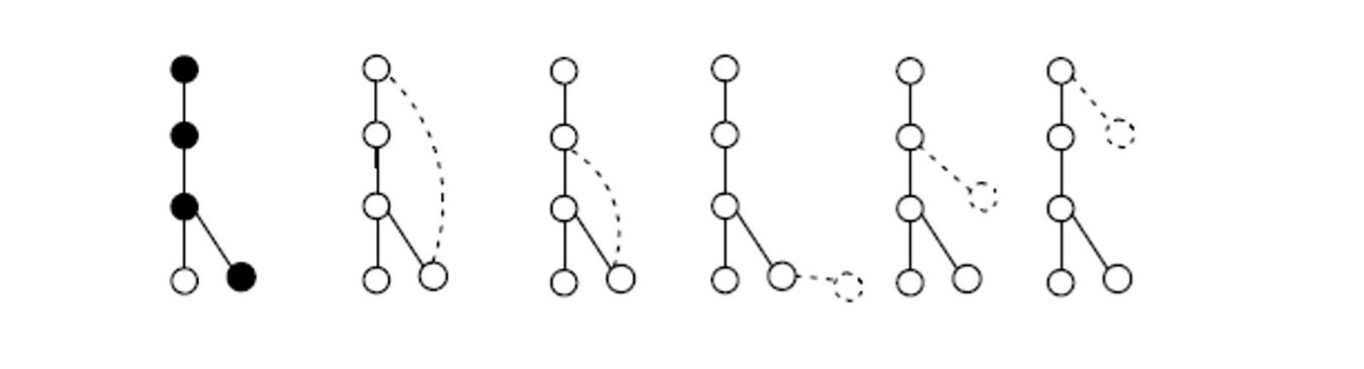
L'albero in figura è prodotto da una visita DFS del grafo frequente. Il cammino evidenziato in nero è il cammino right-most. Nelle due immagini successive si mostra come sia possibile estendere il grafo tramite l'aggiunta di un arco, mentre nelle ultime tre viene aggiunto, in diverse parti del cammino destrorso, un nodo.
1.7 Pruning sulle ridondanze
La generazione dei candidati può portare ad avere sottografi ridondanti, ovvero isomorfi. Occorre una rappresentazione dei grafi che consenta di risolvere abilmente gli isomorfismi. Nella pratica, due rappresentazioni comun sono la matrice di adiacenza e le liste di adiacenza. Tuttavia, tali rappresentazioni non sono adatte ad identificare gli isomorfismi. Osserviamo un esempio di grafi isomorfi la cui matrice di adiacenza è differente:
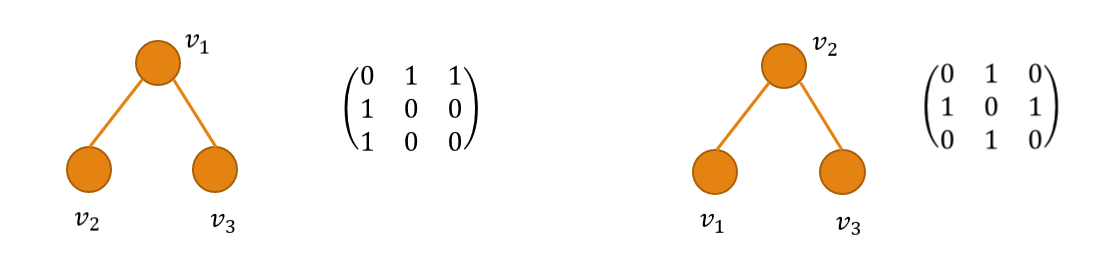
1.7.1 Stringa di adiacenza
Il primo passo verso una rappresentazione ideale è quello di considerare la stringa di adiacenza, ovvero una stringa ottenuta concatenando tutte le righe della matrice di adiacenza o, nel caso di un grafo indiretto, solo le righe appartenenti alla triangolare superiore (a causa della specularità che rende ridondante l'informazione).
Per un grafo con nodi esistono possibili stringhe di adiacenza, ottenute considerando tutte le possibili permutazioni dei nodi. Diverse permutazioni possono produrre la stessa stringa di adiacenza. Non è ancora sufficiente per rappresentare univocamente il grafo.
1.7.2 Forma canonica
La forma canonica di un grafo è la stringa di adiacenza lessicograficamente più piccola (o più grande), tra tutte quelle che si possono ottenere permutando i nodi in tutti e modi possibili. Essa risulta essere una rappresentazione univoca del grafo: due grafi isomorfi hanno la stessa forma canonica.
Per individuare sottografi candidati ridondanti nello step di pruning, occorre calcolare le loro forme canoniche e confrontarle. Se hanno la stessa forma canonica, quindi nel caso di isomorfismo, uno dei due sottografi va escluso.
1.8 Significatività statistica
I sottografi più frequenti non sono necessariamente quelli più rilevanti. Un sottografo frequente potrebbe essere un pattern banale, come un nodo o un arco frequente. Calcolare la significatività statistica di un pattern può essere uno step di post-processamento dei risultati di un algoritmo di FSM, allo scopo di eliminare i pattern banali.
Vediamo come calcolare la significatività del sottografo frequente nel post-processing:
- A partire dal database di grafi, costruire un database formato da grafi random ottenuti a partire da ciascuno dei grafi in .
- Ripetere il primo passo volte, dove è un numero molto grande, ottenendo diversi database di background.
- Per ogni sottografo frequente , calcolare il supporto in ciasuno dei database di background. Al termine di tale passo si otterrà una distribuzione di probabilità dei valori di .
- Calcolare la probabilità di osservare un supporto maggiore o uguale al supporto osservato nel database originale . Chiamiamo tale probabilità p-value.
- Se il p-value è minore di una soglia (tipicamente ), allora è significativo come sottografo frequente.
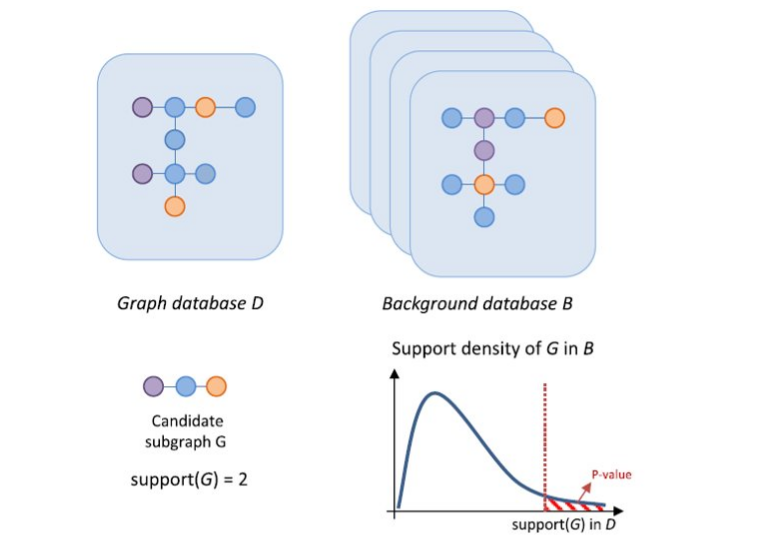
1.8.1 Generazione dei database: Algoritmo edge-swapping
Uno dei metodi più popolari per generare un grafo random a partire da un grafo è l'algoritmo di edge-swapping, che permette di generare un grafo random con la stessa distribuzione di gradi di . L'algoritmo è molto semplice e consiste nei seguenti passi:
- Selezionare casualmente due archi della rete e in modo tale che:
- Gli archi siano disgiunti tra loro, ovvero non abbiano nodi in comune;
- Non esistano in gli archi e ;
- Scambiare le destinazioni dei due archi:
- Iterate i passi un numero sufficiente di volte (convenzionalmente 100 volte il n. totale di archi).
La scelta degli archi al primo passo assicura che al termine di ogni scambio la distribuzione dei gradi rimanga la stessa.
2. Algoritmo FSG
L'algoritmo FSG ha le seguenti caratteristiche principali:
- Strategia Breadth-First Search per trovare i sottografi frequenti
- Metodo join-based per la generazione dei candidati
- Rappresentazione dei sottografi in forma canonica
Osserviamo e commentiamo la procedura dell'algoritmo. Sia il database di grafi, indichiamo con l'insieme di sottografi formati da nodi frequenti in . La prima parte dell'algoritmo calcola semplicemente nodi ed archi frequenti in .
F[1] = tutti i 1-sottografi (nodi) frequenti in D
F[2] = tutti i 2-sottografi (archi) frequenti in D
Dopodiché poniamo e definiamo il passo iterativo. L'iterazione termina quando al passo non viene scovato alcun sottografo frequente.
k = 3
while (F[k-1] non è vuoto) do:
# genera l'insieme dei candidati con k nodi
C[k] = fsg-gen(F[k-1])
# effettuiamo il pruning utilizzando la forma canonica
C[k] = prune(C[k])
# per ogni candidato calcoliamo il supporto (attributo count)
for each candidato G[k] in C[k] do:
G[k].count = 0
for each grafo G in D do:
if (G[k] è sottografo di G) then:
G[k].count = G[k].count + 1
# controlliamo se il supporto è maggiore o uguale alla soglia
if (G[k].count >= sigma) then:
# in tal caso lo aggiungiamo all'insieme dei sottografi
# frequenti con k nodi
F[k].add(G[k])
# incrementiamo il valore di k e passiamo alla
# iterazione successiva
k = k + 1
# ritorniamo tutti gli insiemi frequenti
return {F[1], ..., F[k-2]}
2.1 Generazione dei candidati in FSG
È necessario esplicitare anche alcune procedure arcane utilizzate nella procedura principale, come ad esempio la funzione fsg-gen che genera i sottografi candidati. Essa sarà illustrata e commentata dettagliatamente nel riquadro sottostante.
procedure fsg-gen (F[k])
# inizializziamo l'insieme dei sottografi con k+1 nodi
# candidati
C[K+1] = 0
# per ogni coppia di sottografi i,j nell'insieme F[k]
for each G[i], G[j] in F[k], (i <= j), do:
# inseriamo nell'insieme H tutti i core condivisi
# dai sottografi i e j.
H = get_cores(G[i], G[j])
for each core in H:
# generiamo i possibili candidati con il
# metodo join-based e li inseriamo in B
B = fsg-join(G[i], G[j], core)
# i grafi su cui iteriamo adesso hanno k+1 nodi poiché appena
# generati dalla giunzione di i e j. Verifichiamo per ogni candidato
# la regola Apriori (o chiusura downward).
for each subgraph in B do:
apriori = true
# togliamo un arco alla volta (quindi anche un nodo)
# e verifichiamo se il sottografo formato da k nodi
# risiede nell'insieme F[k]. In caso contrario il grafo
# non è frequente per la regola Apriori.
for each arco e in subgraph do:
# subgraph ha k+1 nodi, k_subgraph ne ha k
# ma conosciamo già l'insieme F[k] dall'input.
k_subgraph = subgraph.removeEdge(e)
if (k_subgraph not in F[k]) then:
apriori = false
break
if apriori == true then:
C[k+1].add(subgraph)
return C[k+1]
2.2 Join tra sottografi
Non resta altro che osservare come viene effettuata la join tra due sottografi che condividono lo stesso core . Ricordiamo che hanno nodi, mentre il core in comune ne ha per definizione .
procedure fsg-join(g[i], g[j], h):
e1 = insieme degli archi presenti in g[i] e non in h
e2 = insieme degli archi presenti in g[j] e non in h
M = insieme di tutti gli automorfismi di h
# inizializziamo l'insieme dei candidati generati
B = 0
# iteriamo su ognuno degli automorfismi del core h
for each automorfismo phi in M do:
# combinando e1, e2, e l'automorfismo phi otteniamo
# vari sottografi di dimensione k+1, conserviamo
# tali sottografi nell'insieme K
K = combine(e1, e2, phi)
B = union(B, K)
return B
2.3 Calcolo della forma canonica
L'algoritmo FSG calcola la forma canonica di ogni sottografo a partire dalla matrice di adiacenza. Osserviamo un esempio per semplicità:
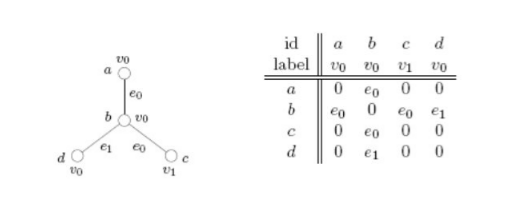
Il primo step consiste nel partizionare ed ordinare i nodi del grafo in base al grado. I nodi hanno grado 1, mentre il nodo ha grado 3. Dividiamo quindi la matrice in due partizioni:
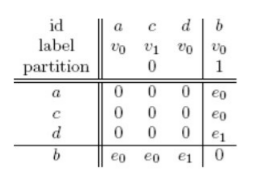
I nodi con grado più alto hanno potenzialmente molti archi asseriti nella matrice. Se disponiamo gli elementi per grado in ordine crescente, allora la stringa di adiacenza risultante avrà la maggior parte degli elementi asseriti verso la fine. Ciò va fatto poiché l'obiettivo è quello di ottenere la forma canonica del sottografo, ovvero la stringa lessicograficamente più piccola.
Se il grafo è etichettato come quello in figura, allora a parità di grado è possibile partizionare ulteriormente l'insieme in base alla etichetta del nodo, disponendo prima le etichette più piccole. Nell'esempio, i nodi hanno rispettivamente etichette . Disponiamo nella prima partizione i nodi di etichette , e in una seconda partizione il nodo di etichetta :
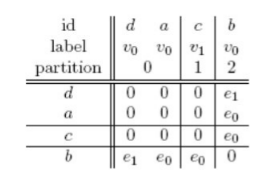
Se in una partizione vi sono più di due nodi, vanno considerate le possibili stringhe di adiacenza date dalla variazione di posizione. Il partizionamento serve soprattutto a diminuire il numero di stringhe di adiacenza da generare. Nel grafo in esempio solo la prima partizione contiene più di un nodo, per cui consideriamo due sole stringhe di adiacenza:

Essendo un grafo non orientato, formiamo le stringhe di adiacenza utilizzando solo le porzioni di righe appartenenti alla triangolare superiore. Nel primo caso avremo , mentre nel secondo caso . Considerando abbiamo che la forma canonica del grafo è quella presentata nel secondo caso.
2.4 Ottimizzazioni
Gli step più pesanti dell'algoritmo dal punto di vista computazionale sono:
- La generazione dei core
- L'operazione di join tra sottografi
- La cancellazione di sottografi candidati poco frequenti
Alcune ottimizzazioni possibili sono rispettivamente:
- Per ogni k-sottografo, memorizzare le forme canoniche dei suoi (k-1)-sottografi frequenti
- Utilizzare schemi di indicizzazione inversa (inverted index)
- Mettere in cache gli automorfismi di core precedenti
2.4.1 Inverted list
Per contare le frequenze degli -sottografi candidati al paso , dovremmo risolvere problemi di subgraph matching, dove è il numero di grafi nel database . La tecnica delle liste invertite può essere utilizzata per ridurre il costo computazionale:
- Ad ogni sottografo frequente è assegnata una TID list (Transaction IDentifier list), ovvero la lista delle transazioni che contengono .
- Per calcolare la frequenza di un -sottografo candidato, viene calcolata l'intersezione delle liste TID dei -sottografi da cui è stato generato.
- Se la dimensione della lista è minore rispetto al supporto minimo, allora il sottografo candidato viene scartato poiché non potrà mai essere frequente, altrimenti si calcola la frequenza solo nelle transazioni della lista prodotta dall'intersezione.
3. Algoritmo gSPAN
L'algoritmo gSPAN ha le seguenti caratteristiche:
- Strategia Depth-First Search per trovare i sottografi frequenti
- Metodo extend-based per la generazione dei candidati
- Rappresentazione dei sottografi con DFS code
3.1 Spazio di ricerca
Lo spazio di ricerca dell'algoritmo gSPAN è un albero gerarchico. Ogni vertice al livello -esimo dell'albero rappresenta un grafo con nodi e possiede un codice definito come DFS code, il cui calcolo approfondiremo in seguito. L'algoritmo utilizza un ordinamento lessicografico per i vertici dell'albero che consente di scoprire sottografi frequenti in maniera efficiente. Vertici con DFS code più piccolo vengono scoperti prima nella ricerca e, nel caso in cui un nodo appena scoperto abbia DFS code analogo ad un altro nodo analizzato precedentemente, si effettua il pruning sul nuovo nodo.
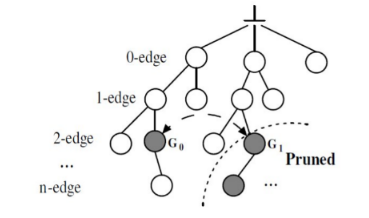
3.2 DFS code
La depth-first search può produrre diversi alberi DFS, come vediamo in esempio:
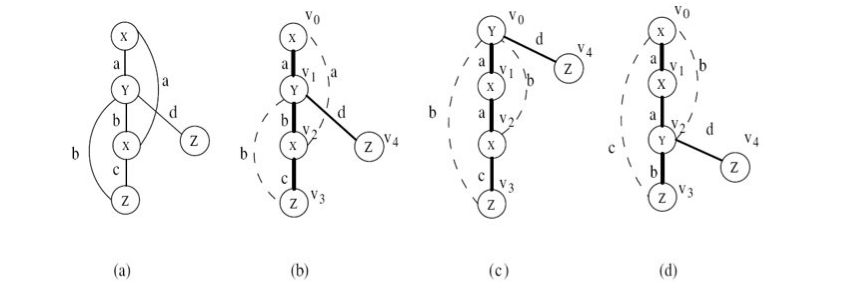
Ognuno dei nodi dell'albero è scoperto ad un tempo differente. Definiamo arco forward un arco che porta da un nodo ad un altro visitato ad un tempo successivo, mentre arco backward un arco che porta da un nodo ad un altro visitato ad un tempo precedente.
Una volta calcolati gli alberi di ricerca DFS è possibile considerare alcuni elementi:
- Vertice right-most, che coincide con l'ultimo nodo visitato;
- Cammino right-most, che va dalla radice al vertice right-most;
- Insieme degli archi forward
- Insieme degli archi backward
Definiamo sequenza DFS la sequenza di nodi ovvero i nodi visitati rispettivamente nei tempi . Essendovi sequenze differenti per ogni albero prodotto, è necessario calcolare una rappresentazione che sia univoca.
A partire dalla sequenza di un albero, definiamo il codice DFS come una sequenza ordinata di archi. Tale sequenza è costruita secondo i seguenti principi:
- Dato un vertice , tutti i suoi archi uscenti backward devono apparire prima degli archi forward
- , ovvero tra gli archi forward viene data precedenza agli archi che portano a nodi visitati prima, ovvero
- , ovvero in generale tra gli archi backward viene data precedenza agli archi che partono da nodi visitati prima
- , ovvero se l'arco backward parte dallo stesso nodo, viene data la precedenza all'arco che termina nel nodo visitato prima.
Una volta generati i codici DFS di tutti gli alberi DFS, attraverso un ordine lessicografico viene determinato il codice DFS minimo ed utilizzato per rappresentare il grafo.
Vediamo un esempio:
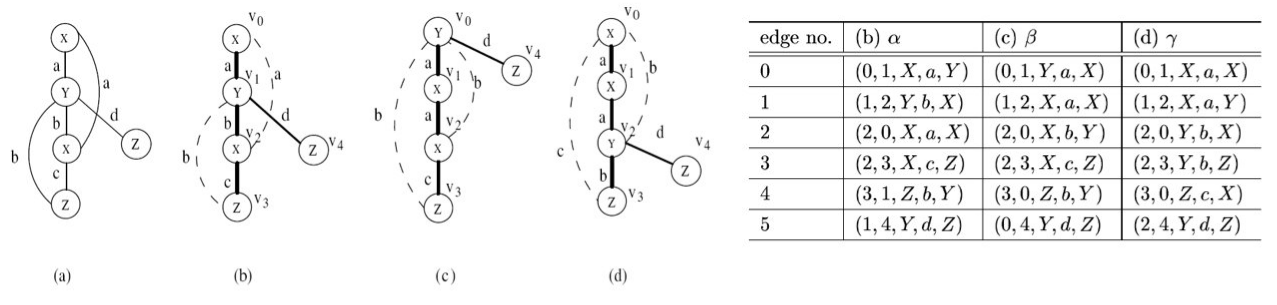
La tabella rappresenta 3 codici DFS prodotti a partire da alberi differenti. Ogni codice è formato da una sequenza di archi rappresentati come quintuple: tempo di scoperta del nodo sorgente, tempo di scoperta del nodo destinazione, etichetta del nodo sorgente, etichetta dell'arco, etichetta del nodo destinazione. Osserviamo come ogni colonna rispetti le regole di ordinamento dettate precedentemente.
A questo punto dobbiamo definire l'ordine lessicografico tra codici differenti, per cui:
- Partendo dal primo arco, si considera il tempo di scoperta dei due nodi e si seleziona il codice con minimo tempo di scoperta.
- A parità di tempi di scoperta, si considera l'ordine lessicografico basato sui restanti 3 campi (etichette).
- A parità di questi, si passa al secondo arco e così via sino a che non si determina il codice minimo.
3.3 Estensione dei sottografi
L'estensione di un sottografo mediante aggiunta di un singolo arco non può essere fatta in maniera arbitraria. Dato un grafo e l'albero DFS con DFS code minimo, due estensioni sono possibili:
- Estensione backward: aggiunta di un arco tra il vertice right-most di T ed uno tra i vertici del cammino right-most.
- Estensione forward: aggiunta di un nuovo nodo e di un arco tra ed un nodo qualsiasi del cammino right-most.
In tal modo il codice DFS del nuovo sottografo figlio nell'albero di ricerca sarà una estensione del codice DFS del sottografo padre. Nello specifico, per ottenere il codice DFS del grafo figlio è sufficiente accodare il nuovo arco al codice DFS del grafo padre. In questo modo, l'algoritmo gSPAN genera meno candidati rispetto ad FSG.
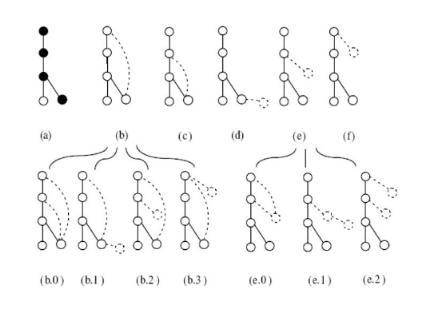
4. Mining in un singolo grafo
Dato un grafo , il problema del mining in un singolo grafo consiste nel trovare tutti i sottografi frequenti in . In questo caso, la frequenza minima è definita in termini di numero di occorrenze di un sottografo in . Un sottografo frequente in un grafo è detto anche motivo.
4.1 Overlap di occorrenze
Nel mining di un singolo grafo ci sono due modi di contare le occorrenze di un sottografo:
- Senza sovrapposizioni (no overlaps)
- Con sovrapposizioni di nodi o archi (with overlaps)
Nel primo caso continua a valere la regola Apriori, mentre nel secondo caso potrebbe non valere.
Osservando l'esempio sottostante ci accorgiamo che il sottografo ha un supporto pari ad 1 nel grafo . Si noti che è contenuto nel sottografo : se vale la regola Apriori, dovrà avere un supporto minore o uguale a quello di . Considerando il mining con overlap, il grafo avrà supporto 2 in , per cui non vale la regola apriori.
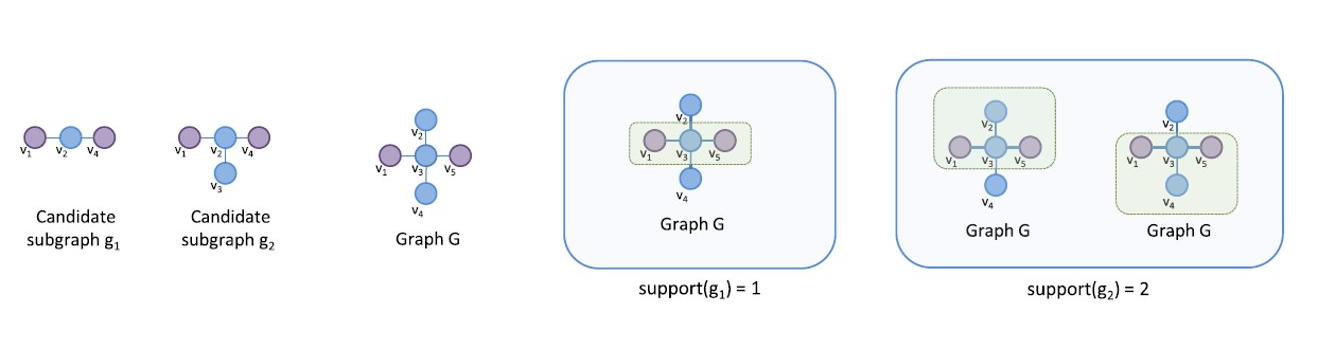
4.2 Significatività statistica
Nel problema del mining in un singolo grafo (o ricerca di motivi) raramente si considera solo il numero di occorrenze per valutare se un sottografo è un motivo.
Si definisce motivo un sottografo ricorrente che è significativamente sovra-rappresentato in una rete.
La significatività la si può calcolare usando la stessa procedura descritta in precedenza, creando un insieme di varianti random del grafo e contando la frequenza del sottografo in ognuna delle varianti random. Il -value ottenuto a partire dalla distribuzione delle frequenze di determina la significatività statistica del motivo.
Sono stati recentemente sviluppati dei modelli per calcolare analiticamente il -value senza generare le varianti random, velocizzando il calcolo della significatività.
4.3 Strategie di ricerca
Attraverso un generico grafo è possibile estrarre un numero molto grande di sottografi considerando tutte le varie combinazioni. È necessario definire delle strategie intelligenti per effettuare la ricerca dei motivi in maniera efficiente.
4.3.1 Strategia network-centric
Vengono ricercati ed enumerati tutti i possibili sottografi con nodi che occorrono nella rete iniziale. Si raggruppano attraverso un match dell'isomorfismo le occorrenze di sottografi differenti che hanno la stessa struttura.
Il vantaggio principale della strategia è che sottografi che non occorrono in non verranno mai considerati. Così facendo risulta più efficiente l'analisi di grafi di grosse dimensioni. Tuttavia, il censimento dei sottografi è un processo molto costoso.
4.3.2 Strategia motif-centric
Vengono enumerati tutti i possibili sottografi con nodi e vengono ricercati in separatamente. In tal modo la verifica di un sottografo come motivo è diretta, ma l'enumerazione di tutti i sottografi con nodi diventa esponenzialmente proibitiva all'aumentare di . Tale approccio è ottimo per grafi di piccola dimensione.
4.3.3 Strategia set-centric
La strategia set-centric è un ibrido tra le due precedenti. Consiste nel ricercare un insieme di sottografi e, con una unica passata sul grafo , trovare tutti i match dei sottografi e raggruppare i match isomorfi.
4.4 Ricerca esatta vs Sampling
Effettuare una ricerca esatta significa enumerare esaustivamente tutti i sottografi con nodi. Una strategia alternativa è quella del sampling, che consiste nel campionare randomicamente un adeguato numero di sottografi con nodi. Dopodiché vengono conteggiate le frequenze dei campioni.
La procedura per effettuare il sampling è la seguente:
- Si sceglie un seed iniziale, ovvero un nodo o un arco casuali in .
- Si estende il seed iterativamente (con archi o nodi) sino a raggiungere un sottografo di nodi.
Il sottografo campionato è definito dall'insieme dei nodi e da tutti gli archi che li collegano. Una variante di sampling consiste nel campionare opportunamente una sottorete di ed effettuare una ricerca esatta in , stimando i -values per i motivi di su .
Il sampling, con poche migliaia di campioni, può ottenere risultati veloci ed accurati. Inoltre non risulta sensibile alla dimensione della rete. Potrebbero tuttavia riscontrarsi bias ed alcuni motivi significativi potrebbero sfuggire.
Catene di Markov e Hidden Markov Models
1. Catene di Markov
Una catena di Markov è una tripla dove:
- è un insieme finito di stati (o eventi).
- denota lo stato osservato all'i-esimo istante di tempo.
- rappresenta l'insieme delle probabilità iniziali per ogni stato.
- è l'insieme delle probabilità di transizione denotate da per ogni .
Nello specifico, denota la probabilità che all'istante di tempo si verifichi lo stato dato per assunto che all'istante di tempo si sia presentato lo stato . Di fatto si parla di una transizione di stati e si rappresenta attraverso il concetto di probabilità condizionata:
Sia n la cardinalità dell'insieme degli stati , l'insieme è esprimibile attraverso una matrice, chiamata matrice di transizione di dimensione , dove l'elemento rappresenta la probabilità di passare dallo stato allo stato .
1.1 Proprietà memoryless
Generalemente si parla di catene di Markov del primo ordine quando lo stato successivo dipende esclusivamente dallo stato corrente. Tale proprietà prende il nome di proprietà memoryless. Formalmente, se è la sequenza di stati osservati, si ha: Quindi la probabilità che all'istante di tempo si abbia dipende solo dal fatto che allo stato . Tale probabilità è esprimibile attraverso la transizione tra lo stato e lo stato , ovvero .
1.2 Probabilità di una sequenza di eventi
Consideriamo la seguente catena di Markov (immagine sottostante) dove i nodi rappresentano i possibili stati e gli archi le transizioni possibili con le rispettive probabilità. Supponiamo di osservare una sequenza di stati del genere: con probabilità iniziali . Come calcoliamo la probabilità che si verifichi tale sequenza?
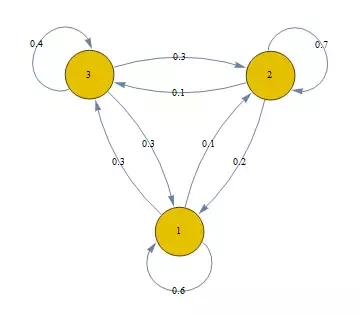
Vogliamo quindi calcolare la probabilità , che risulta essere una probabilità congiunta. In generale, per le proprietà sul prodotto logico tra eventi si ha: Ma ricordiamo che vale la proprietà memoryless, per cui: Applichiamo tali concetti alla sequenza d'esempio e otteniamo:
1.3 Matrice stocastica
Nella matrice di transizione di una catena di Markov la somma degli elementi di ciascuna riga è uguale ad 1, ovvero da ciascuno stato è sempre possibile raggiungere uno qualsiasi degli stati della catena (anche stesso), e la somma delle probabilità di transizione è 1. In virtù di tale proprietà la matrice di transizione è detta stocastica. Vediamo la matrice di transizione della catena in esempio:
| Stato 1 | Stato 2 | Stato 3 | |
|---|---|---|---|
| Stato 1 | 0.6 | 0.1 | 0.3 |
| Stato 2 | 0.2 | 0.7 | 0.1 |
| Stato 3 | 0.3 | 0.3 | 0.4 |
1.4 Classificazione delle catene di Markov
Una catena di Markov si dice irriducibile se da ogni stato è possibile raggiungere un qualsiasi altro stato della catena mediante una o più transizioni.
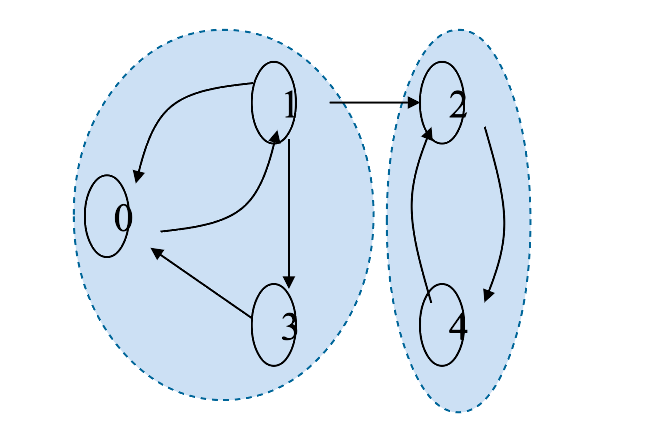
Definiamo periodo di uno stato come il minimo numero di passi necessari per tornare ad con probabilità non nulla. Se il periodo è maggiore di 1, lo stato è detto periodico. Una catena di Markov aperiodica è una catena in cui nessuno stato è periodico.
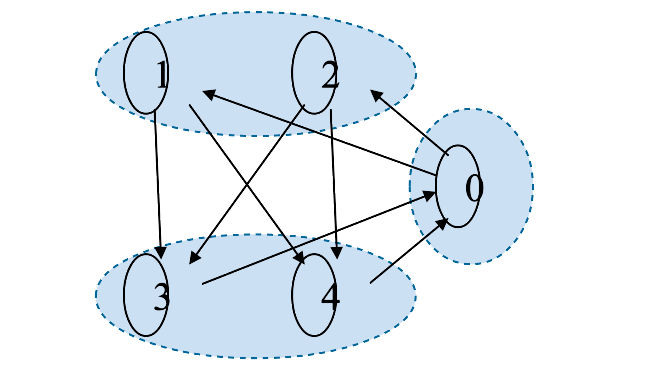
1.5 Probabilità di eventi successivi
Prendiamo in considerazione la seguente catena di Markov:
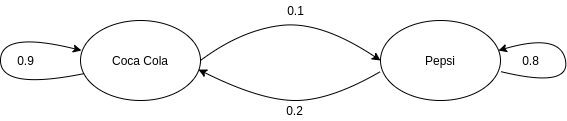
Essa indica che una persona che compra Coca-Cola nel 90% dei casi la prossima volta comprerà Coca-Cola. Se una persona compra Pepsi allora nell'80% dei casi la prossima volta comprerà Pepsi. Visualizziamo la matrice di transizione:
| Coca Cola (C) | Pepsi (P) | |
|---|---|---|
| Coca Cola (C) | 0.9 | 0.1 |
| Pepsi (P) | 0.2 | 0.8 |
Domanda: per una persona che attualmente compra Pepsi, qual è la probabilità che tra due volte acquisterà Coca Cola?
La probabilità richiesta è esprimibile come: Tuttavia lo stato a tempo dipende solo dallo stato , che può essere sia Coca-cola che Pepsi. Essendo due casi favorevoli, vanno considerati entrambi e vanno sommate le probabilità. Per cui adesso necessitiamo di: Calcoliamo entrambe le probabilità attraverso la matrice di transizione: Calcoliamo la somma delle due probabilità: Osservazione Se effettuiamo il prodotto riga colonna tra la matrice A e se stessa otterremo un'ulteriore matrice della stessa dimensione, dove ogni elemento indica la probabilità di due transizioni, la cui transizione di mezzo può essere uno qualsiasi tra gli stati. Di fatto l'elemento di indici indica la probabilità che, partendo dallo stato si possa arrivare allo stato in due transizioni con probabilità del 34%.
A questo punto è possibile generalizzare il concetto: per una persona che compra Coca Cola, qual è la probabilità che tra n volte comprerà Pepsi? Allora basterà effettuare il prodotto riga colonna della matrice A con se stessa per n volte.
Sia la distribuzione di probabilità iniziale. Ogni qual volta effettuiamo un prodotto riga-colonna otteniamo una distribuzione differente. Si può dimostrare che ad un certo punto si arriverà ad una distribuzione stazionaria in cui le probabilità non varieranno.
1.5.1 Distribuzione stazionaria
Sia una catena di Markov del primo ordine, irriducibile e aperiodica con k stati. Si dimostra che: Tale proprietà vale per tutti gli , dunque si ottiene un vettore di valori . Se contiene valori non nulli, allora è detta distribuzione stazionaria. Se tutti i valori di sono non nulli allora è l'unica distribuzione stazionaria.
2. Hidden Markov Models (HMM)
Un modello di Markov nascosto (in inglese Hidden Markov Model o HMM) è un modello più ricco rispetto alla catena di Markov. A differenza di una catena di Markov, in un HMM gli stati sono nascosti. Ogni stato emette un simbolo con una certa probabilità. L'osservatore vede soltanto una sequenza di simboli emessi in base alla quale può dedurre la probabilità di osservare la corrispondente sequenza di stati associati.
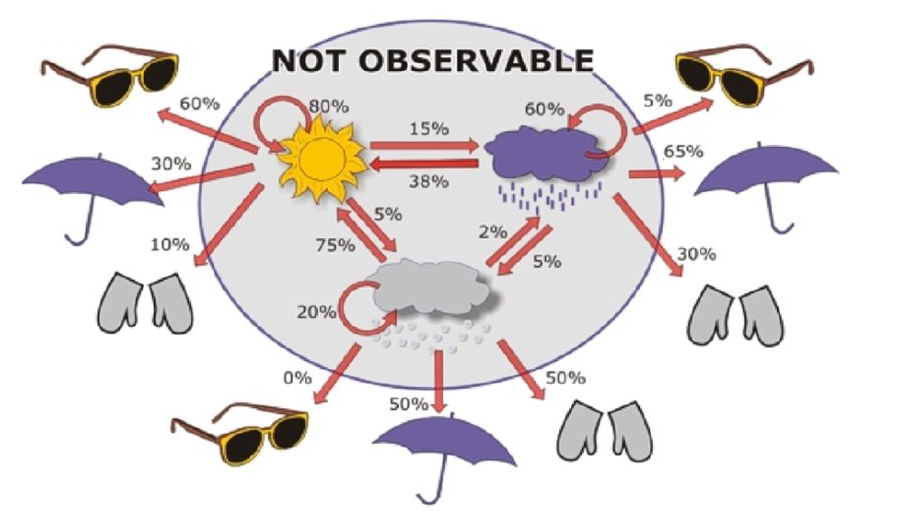
2.1 Definizione
Una Hidden Markov Model è una quintupla dove:
- è un insieme finito di stati (o eventi).
- denota lo stato osservato all'i-esimo istante di tempo.
- rappresenta l'insieme delle probabilità iniziali per ogni stato.
- è la matrice delle probabilità di transizione denotate da per ogni .
- è un alfabeto composto da m simboli.
- denota il simbolo emesso all'i-esimo istante di tempo.
- è la matrice di emissione di dimensione contenente per ogni stato e ogni simbolo la probabilità che emetta . Si scrive:
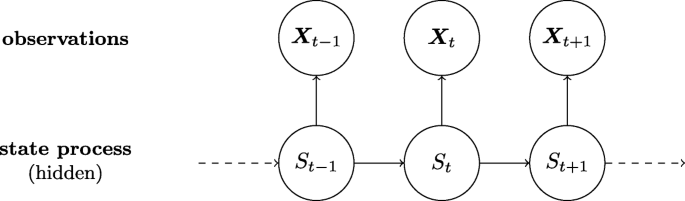
2.2 Problemi principali su HMM
I problemi principali legati alle Hidden Markov Models sono i seguenti:
- Evaluation: Sia un HMM ed X una sequenza di simboli, calcolare la probabilità della sequenza.
- Decoding: Sia un HMM ed X una sequenza di simboli, trovare la sequenza di stati che massimizza .
- Learning: Sia M un HMM con probabilità di transizione e di emissione note, ed una sequenza , trovare i parametri del modello che massimizzano .
Esempio: Ipotizziamo che in un casinò vi sia un croupier disonesto con due dadi, uno regolare ed uno truccato. Il dado regolare ha equiprobabilità nell'emettere un qualsiasi numero tra 1 e 6; il dado truccato ha una probabilità maggiore di emettere 6 rispetto agli altri numeri. Data una sequenza di lanci risolvere i seguenti problemi:
- Evaluation: Nota la HMM, qual è la probabilità di ottenere questa sequenza di risultati?
- Decoding: Quando il croupier ha utilizzato il dato regolare e quando quello truccato?
- Learning: Quali sono le matrici di transizione ed emissione che massimizzano la probabilità di ottenere questi risultati?
2.3 Evaluation
Dato un HMM ed una sequenza di simboli qual è la probabilità di ottenere tale sequenza?
Supponiamo di fissare la sequenza di stati (incognita). La probabilità di osservare gli n simboli della sequenza emessi dagli n stati di è data da: Ci avvaliamo delle proprietà sul prodotto logico, per cui: Supponendo che la catena di Markov sia del primo ordine, allora esprimiamo il primo fattore del prodotto come: Osserviamo il secondo fattore: ci accorgiamo che la probabilità di emettere il simbolo dipende solo dallo stato , per cui è possibile scomporre tutto in un semplice prodotto di probabilità condizionate: Ma corrisponde alla elemento della matrice di transizione e corrisponde all'elemento della matrice di emissione, per cui riscriviamo l'espressione finale come segue:
2.3.1 Probabilità forward
Nel ragionamento precedente abbiamo assunto una sequenza di stati . Tuttavia per ottenere la probabilità della sequenza data è necessario sommare le probabilità date da tutte le sequenze possibili di stati che possono emettere la data sequenza: Per evitare la somma, che coinvolge un numero esponenziale di sequenze di stati , definiamo: La funzione è chiamata probabilità forward, ovvero la probabilità di osservare una sequenza di simboli emessi da una sequenza di stati tale che il t-esimo stato (stato al tempo t) sia .
È possibile calcolare la probabilità forward in maniera induttiva, dove il caso base corrisponde a: Mentre il passo induttivo è il seguente: Il passo induttivo deriva dal fatto che allo stato al tempo ci si possa arrivare da uno qualunque degli stati precedenti visitato al tempo , dopo avere emesso i simboli . Per arrivare allo stato da effettuo una transizione , ed infine si emette il simbolo corrispondente .
A partire dalla probabilità forward, possiamo ottenere la probabilità finale come: Ricordando che k è il numero di stati ed n è la lunghezza della sequenza .
Applicare l'algoritmo forward equivale a percorre tutti i possibili cammini di un particolare tipo di grafo, chiamato lattice, dove i k stati sono disposti in colonna e ripetuti n volte:
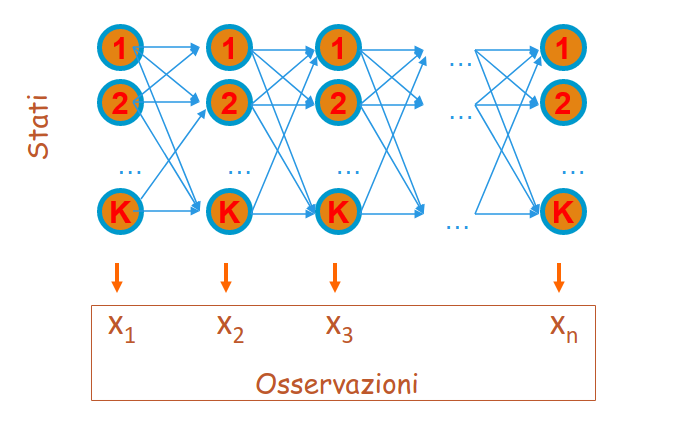
2.3.2 Algoritmo forward
Dalle precedenti relazioni segue il seguente algoritmo di programmazione dinamica con complessità , dove k è il numero di stati ed n è la lunghezza della sequenza .
X # array contenente la sequenza di simboli emessi
k # numero di stati
f # matrice delle probabilità forward,
# dove nelle righe risiedono i tempi e nelle colonne gli stati
E # matrice delle emissioni
A # matrice delle transizioni
# passo base
for i = 1 to k:
f[1,i] = P(pi_1 = i) * E[pi_1, i]
# passo induttivo
for t = 1 in len(X):
# per ogni stato j
for j = 1 to k:
sum = 0
# calcolo la probabilità di passare
# da uno qualsiasi tra gli stati
# precedenti i a j
for i = 1 in k:
sum = sum + f[t,i] * A[i,j]
# dopodiché moltiplico per la probabilità
# di emettere il simbolo x_{t+1}
simbol_to_emit = X[t+1]
f[t+1, j] = sum * E[j, simbol_to_emit]
# calcolo la probabilità finale sommando
# l'ultima riga della matrice, che conterrà
# le probabilità forward al tempo n per tutti
# gli stati.
p = 0
n = len(X) - 1
for i = 1 in k:
p = p + f[n, i]
return p
2.4 Decoding
Il secondo problema da affrontare è il decoding. Data una HMM ed una sequenza di simboli trovare la sequenza di stati che massimizza la probabilità congiunta di osservare gli simboli emessi dagli n stati di : Dove dai calcoli precedenti sappiamo che:
2.4.1 Algoritmo di Viterbi
L'algoritmo di Viterbi ha una struttura simile a quella dell'algoritmo forward. Tuttavia, anziché sommare i contributi provenienti da ogni singolo stato visitato al passo precedente, seleziona di volta in volta il contributo migliore, ovvero quello con il valore massimo. Ciò equivale nel lattice a tracciare un cammino di stati di lunghezza n che massimizzi la probabilità di ottenere la sequenza :
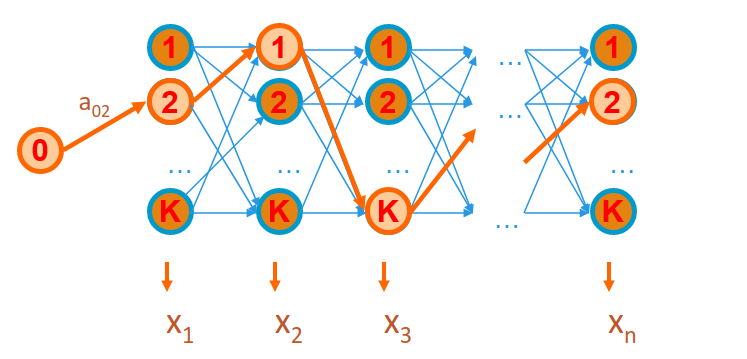
Definiamo una funzione : Come nel caso della probabilità forward, anche la funzione è definita per induzione, per cui definiamo prima il caso base: Mentre il passo induttivo è il seguente: Il passo induttivo deriva dal fatto che allo stato al tempo ci si possa arrivare da uno qualunque degli stati precedenti visitato al tempo , ma si seleziona solo lo stato con la probabilità maggiore dopo avere emesso i simboli . Per arrivare allo stato da effettuo una transizione , ed infine si emette il simbolo corrispondente .
A partire dalla funzione possiamo calcolare la probabilità finale come segue:
2.4.2 Pseudocodice dell'algoritmo
X # array contenente la sequenza di simboli emessi
k # numero di stati
V # matrice Viterbi, dove nelle righe risiedono i tempi e nelle colonne gli stati
E # matrice delle emissioni
A # matrice delle transizioni
phi # matrice per tener traccia del cammino
# dove nelle righe risiedono i tempi e nelle colonne gli stati
# passo base
for i = 1 in k:
V[1,i] = P(pi_1 = i) * E[pi_1, i]
phi[0, i] = 0
# passo induttivo
for t = 1 in len(X):
# per ogni stato j
for j = 1 in k:
_max = 0
phi[t, j] = 0
# cerco tra tutti i percorsi calcolati
# precedentemente quello con la probabilità
# maggiore di passare allo stato j-esimo
for i = 1 in k:
if (V[t, i] * A[i,j] > _max):
_max = V[t, i] * A[i,j]
phi[t,j] = i
# dopodiché moltiplico per la probabilità
# di emettere il simbolo x_{t+1}
simbol_to_emit = X[t+1]
V[t+1, j] = _max * E[j, simbol_to_emit]
# cerco quale tra i cammini di lunghezza n calcolati
# abbia probabilità maggiore di emettere gli n simboli
pmax = 0
n = len(X) - 1
for i = 1 in k:
if (V[n,i] > pmax):
pmax = V[n,i]
phi[n,i] = i
# ricostruisco il cammino attraverso i valori di phi
decoded_sequence = retrieve_path(phi)
2.4.3 Recuperare la sequenza di stati
Mediante la struttura dati si tiene traccia, ad ogni istante di tempo , degli stati migliori da cui si può provenire raggiungendo ogni stato del modello. In particolare, indica lo stato migliore da cui si può partire al tempo per raggiungere lo stato al tempo . Partendo dallo stato che massimizza , andando a ritroso, è possibile recuperare la sequenza completa degli stati che massimizza la probabilità finale di osservazione della sequenza di simboli.
2.5 Posterior Decoding
Il posterior decoding è un particolare problema di decoding. Avendo osservato una intera sequenza di simboli , si vuole calcolare (a posteriori) lo stato più probabile all'istante , ovvero lo stato tale che
Ma osserviamo che:
Il problema di massimizzazione è analogo se anziché il rapporto consideriamo solo la probabilità congiunta al numeratore, che tra l'altro possiamo esplicitare:
Dalle proprietà sul prodotto logico tra probabilità abbiamo:
Dove l'ultima semplificazione è possibile grazie alla proprietà memoryless delle catene di Markov del primo ordine. Il primo fattore del prodotto finale altro non è che la forward probability per , mentre il secondo fattore prende il nome di backward probability.
2.5.1 Probabilità backward
La probabilità di backward è la probabilità che si abbia una sequenza di simboli emessa da una sequenza di stati, dato per assodato che . Il ragionamento è analogo a quello dedotto dalla probabilità forward, per cui è possibile procedere per induzione:
Il passo base si ha quando , ovvero si effettua la supposizione . Ma osserviamo che non vi è nessuna sequenza da calcolare dato che n è la lunghezza massima della sequenza in input, per cui la probabilità sarà massima, .
Passo induttivo: Possiamo scomporre l'espressione: Essendo che ad ogni iterazione della sommatoria lo stato è fissato a , possiamo rimuovere dalla probabilità l'emissione dell'elemento (che sarà banalmente emesso dallo stato ) e la transizione dallo stato allo stato e moltiplicarli singolarmente: Ci accorgiamo che la probabilità corrisponde alla probabilità backward calcolata per , per cui sostituendo:
2.5.2 Algoritmo backward
Analogo all'algoritmo forward, l'algoritmo backward ha complessità , dove k è il numero di stati ed n è la lunghezza della sequenza .
# Sia X un array di lunghezza n contenente la sequenza di simboli emessa
# Sia B (Backward) una matrice le quali righe indicano i tempi, mentre le colonne gli stati
# Sia Q l'insieme di stati di cardinalità k
# Sia E la matrice d'emissione e A la matrice delle transizioni
def backward_probability(X, Q, Sigma):
n = len(X) - 1 # partiamo da 0
k = len(Q) - 1 # partiamo da 0
# passo base
for i in range(0, k):
B[n, i] = 1
# passo induttivo
# per ogni simbolo in sequenza, partendo dal penultimo
# poiché l'ultimo è coperto dal passo base
for t in range(0, n-1, -1): # da n-1 a 0
# eseguiamo il calcolo per ogni stato
for i in range(0, k):
probability = 0
# allo stato i ci si può arrivare attraverso
# uno stato qualsiasi tra i k stati disponibili
for j in range(0, k):
# prendo la probabilità del tempo t+1
# poiché l'algoritmo va a ritroso
symbol_emitted = X[t+1]
probabilty_to_add = B[t+1] * A[i,j] * E[j, symbol_emitted]
probability = probability + probability_to_add
# aggiorniamo il valore della backward probability
# per lo stato i-esimo esaminato al tempo t
B[t,i] = probability
# calcoliamo la probabilità finale sommando tutti
# gli stati più vicini allo stato t, ovvero quelle
# a tempo t = 1 (in codice = 0)
backward_probability = 0
for i in range(0, k):
backward_probability = backward_probability + B[0,i]
return backward_probability
2.6 Learning
Il terzo problema è quello del learning e si divide in due scenari a seconda se la risposta esatta è nota o meno, ovvero se si conosce la sequenza di stati relativa alla sequenza di simboli in input.
2.6.1 Primo scenario: risposta esatta nota
Sia la sequenza di simboli per i quali la corrispondente sequenza nascosta di stati è nota . Siano i simboli distinti nell'alfabeto e gli stati finiti in , nella HMM . Definiamo:
- = numero di volte che la transizione dallo stato allo stato si presenta in .
- = numero di volte che lo stato s in emette il simbolo nella sequenza .
Si dimostra che i parametri che danno il massimo sono le matrici di transizione ed emissione le cui entry sono date da:
Tuttavia, pochi dati in input possono essere insufficienti per una stima corretta. Quindi è possibile ricadere nel problema dell'overfitting.
2.6.2 Secondo scenario: risposta esatta non nota
Dato che non si è a conoscenza della sequenza di stati, l'idea è quella di partire assegnando valori randomici alle matrici ed ed aggiornare i parametri del modello in base alla conoscenza che si ha in un certo momento. Viene ripetuto il processo sinché non si soddisfa un criterio di terminazione. Tale principio prende il nome di Expectation-Maximization (EM).
Expectation Maximization
Il principio si basa sui seguenti passi:
- Stimare e dai dati osservati utilizzando i valori correnti ed delle matrici di transizione ed emissione;
- Aggiornare i parametri delle matrici ed in base ad e ;
- Ripetere i primi due passi sino a che il processo non converge.
2.6.3 Algoritmo Baum-Welch
L'algoritmo di Baum-Welch è un algoritmo di tipo Expectation-Maximization. Definiamo: Data la sequenza di simboli , tale espressione esprime la probabilità a posteriori che lo stato e che lo stato successivo . Osserviamo il lattice associato:
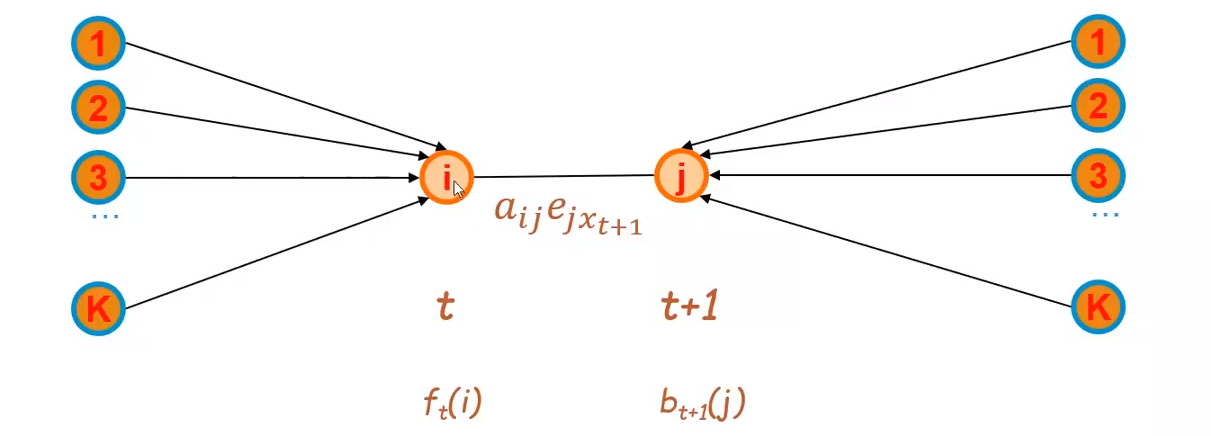
Possiamo calcolare la probabilità che si arrivi allo stato attraverso un percorso qualsiasi attraverso la probabilità forward, mentre calcoliamo la probabilità di arrivare al tempo tale che provenendo, al tempo , da uno qualunque dei stati attraverso la probabilità backward. È necessario considerare anche la transizione da a e l'emissione del simbolo . Essendo una probabilità, bisogna normalizzare il valore ottenuto tra 0 ed 1. È necessario quindi dividere il risultato per la somma di risultati ottenuti considerando la stessa espressione per ogni possibile coppia di stati . Introduciamo un'ulteriore quantita , ovvero la probabilità a posteriori di trovarsi al tempo nello stato : Possiamo stimare la probabilità di transizione come il rapporto tra il numero di volte in cui passiamo dallo stato allo stato ed il numero di volte in cui passiamo dallo stato ad un qualsiasi altro stato: Possiamo stimare la probabilità di emissione come il rapporto tra il numero di volte in cui dallo stato emetto il simbolo e il numero di volte in cui entro nello stato (emettendo un simbolo qualsiasi): I passi dell'algoritmo sono i seguenti:
- Inizializzazione:
- inizializza ed randomicamente (o in base ad una conoscenza pregressa)
- Iterazione
- Calcola le probabilità forward
- Calcola le probabilità backward
- Aggiorna i parametri del modello calcolando le stime e
- Calcola la probabilità di osservare la sequenza di simboli con i parametri
- Itera nuovamente sino a che varia poco rispetto al valore precedente
La probabilità è calcolabile banalmente poiché ricade nel problema dell'evaluation già affrontato.
L'algoritmo non garantisce di trovare i migliori parametri e può convergere a minimi locali in base alle condizioni iniziali. Sia b il numero di iterazioni, la complessità è .
Sistemi di raccomandazione
1. Introduzione
I sistemi di raccomandazione sono una classe di sistemi che implicano la predizione delle risposte dell'utente a delle opzioni, o in generale, le preferenze di un utente rispetto a specifici oggetti (items) sulla base delle preferenze espresse in passato. L'idea principale dietro i sistemi di raccomandazione è la seguente:
- L'utente interagisce con gli oggetti;
- In base a tali oggetti, il sistema crea un modello di preferenze per l'utente;
- Il modello permette di predire la reazione dell'utente a nuovi oggetti;
- Il sistema cerca quali oggetti sono potenzialmente interessanti per l'utente;
- Il sistema raccomanda oggetti interessanti all'utente;
1.1 Tassonomia
Esistono due principali gruppi di sistemi di raccomandazione:
- Sistemi content-based, che effettuano suggerimenti ad un utente sulla base delle proprietà di altri item con cui l'utente ha interagito.
- Sistemi collaborative filtering, che effettuano suggerimenti ad un utente sulla base degli item piaciuti ad utenti ad esso simili.
1.2 Fenomeno long tail
Lo spazio limitato dei negozi fisici spinge i negozianti all'esposizione della merce più popolare, che risulta vendibile con maggiore frequenza. Tale scelta emargina prodotti di nicchia, come film di autori novelli o dischi di band underground. Un sistema di raccomandazione prende in considerazione un numero di prodotti maggiore di almeno 2 o 3 ordini di grandezza rispetto a quelli esposti in un negozio fisico.
Gli articoli sono generalmente caratterizzati da una distribuzione a coda lunga per la quale solo un piccolo insieme di articoli ha maggiore popolarità, mentre un ampio insieme di articoli costituisce una nicchia, che spesso non è nemmeno conosciuta dai clienti. Mentre i negozi fisici tendono a utilizzare tutto lo spazio sugli scaffali per posizionare gli articoli più popolari, i negozi digitali non soffrono di tale problema e possono spingere verso una maggiore variabilità dei contenuti. Di conseguenza, c'è un insieme di prodotti poco popolari che si possono trovare solo online, non convenienti da vendere in un negozio fisico.
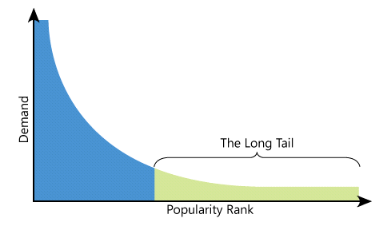
I rivenditori digitali possono facilmente esplorare la distribuzione a coda lunga perché non hanno alcun vincolo fisico (spazio sugli scaffali), ma come fanno a far conoscere agli utenti i prodotti di cui non sono a conoscenza perché non sono abbastanza popolari? Lo strumento più ambito a questo scopo è il sistema di raccomandazione, che può guidare gli utenti da un item popolare ad uno meno popolare con caratteristiche simili.
1.2.1 Alcuni svantaggi
Un sistema di raccomandazione necessita di molti dati per funzionare correttamente. Più informazioni si conoscono sulle preferenze degli utenti, più è accurata la predizione. In alcuni contesti, ad esempio nell'informazione e nei social media, un sistema di raccomandazione può essere utilizzato ai fini di consenso e propaganda per orientare gli utenti verso un'opinione: può scaturire una mancanza di opinione critica sui fatti.
1.3 Definizione del problema
Sia l'insieme degli utenti ed l'insieme degli item. Lo scopo di un sistema di raccomandazione è quello di assegnare un valore ad una coppia - che quantificherà quanto all'utente possa piacere l'item . Definiremo quindi una utility function (funzione di utilità) come segue: Dove è l'insieme del rating, ovvero un insieme totalmente ordinato. Esistono molte varianti di rating:
- rating compreso tra stelle
- rating normalizzato compreso in
- rating binario (mi piace, non mi piace)
1.3.1 Matrice di utilità
Un sistema di raccomandazione si basa su un insieme di preferenze conosciute espresse da utenti per oggetti o item, che può essere rappresentato da una matrice di utilità (talvolta chiamata ). La matrice è una matrice - dove l'i-esima riga rappresenta l'utente , l'i-esima colonna rappresenta l'item ed ogni elemento della matrice rappresenta il rating dell'utente rispetto all'item .
Essa rappresenta la conoscenza esistente del sistema sulla relazione tra utenti ed articoli ed è perlopiù sparsa poiché un generico utente recensisce / interagisce con pochi item. Un sistema di raccomandazione vuole predire i valori di rating inesistenti della matrice.
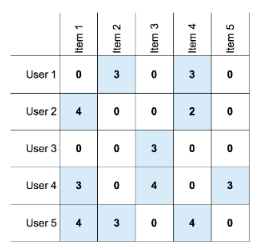
1.4 Problematiche chiave
Quando progettiamo un sistema di raccomandazione, incontreremo due problemi principali: la popolazione della matrice di utilità e la predizione di rating non ancora conosciuti.
1.4.1 Popolare la matrice di utilità
Se la matrice di utilità è vuota, è impossibile effettuare delle raccomandazioni. Ci sono due metodi pincipali per popolare la matrice di utilità: metodo esplicito e metodo implicito. I due approcci possono essere utilizzati in contemporanea.
L'approccio esplicito consiste nel chiedere all'utente di recensire gli item (i.e. Netflix ai nuovi utenti). Tuttavia, questo approccio stanca ed infastidisce facilmente gli utenti, che potrebbero cambiare piattaforma o inserire suggerimenti casuali. Inoltre, le valutazioni sono generalmente influenzate dal fatto che sono fornite da persone disposte a fornirle (che di solito è una piccola parte dell'intero gruppo di utenti).
L'approccio implicito fa inferenza dal comportamento dell'utente. Ad esempio lo storico delle visite a certi item, lo storico degli acquisti, le interazioni con l'oggetto etc. In generale, lo storico di ricerca è utilizzato per fare inferenza sulle categorie di item di interesse.
2. Sistemi Content-Based
L'idea principale dietro i sistemi Content-Based è quella di raccomandare all'utente degli item simili ad item recensiti precedentemente con un buon rating. Ad esempio:
- Raccomandare film con gli stessi attori, dello stesso regista o dello stesso genere.
- Raccomandare news con contenuto simile (i.e. politica, cucina, sport)
Step 1. Dato un utente, il punto di partenza è costituito dagli item da esso recensiti. Ogni item è descritto da vari attributi. Per ogni item recensito viene costruito un profilo, ovvero un vettore di valori dove ogni valore è riferito ad un attributo. Ipotizziamo che gli item siano film, allora gli attributi possono essere i vari generi (thriller, romantico, horror, azione, etc).
Step 2. Viene costruito uno user profile (profilo dell'utente) a partire dai profili degli item recensiti, che rappresenti il grado medio di preferenza dell'utente rispetto ai vari attributi. Ad esempio, l'utente potrebbe preferire film di azione e romantici e valutare negativamente gli horror.
Step 3. Dato un item non ancora recensito dall'utente, viene generato il profilo dell'item e confrontato con lo user profile. Da una certa nozione di similarità tra profili si inferisce se all'utente possa piacere o meno l'item.
I problemi più rilevanti sono: la scelta delle proprietà principali, la costruzione del profilo utente, il calcolo della similarità tra due profili.
2. 1 Definizione formale
Si supponga che tra le proprietà degli item se ne selezionino più rilevanti .
Per ogni item valutato dall'utente viene costruito un profilo , ovvero un vettore tale che: Si costruisce il profilo dell'utente , ovvero il vettore di valori , dove il generico elemento rappresenta il grado medio di preferenza dell'utente per gli item recensiti che possiedono la proprietà . Sia un item non ancora recensito da e di cui si vuole predire la preferenza. Si genera il profilo dell'item e si calcola la similarità tra i profili ed . Se la similarità è alta, allora si consiglia ad l'item .
2.2 Profilo di un item
Il profilo di un item descrive quali proprietà contiene un item. Le proprietà rappresentano categorie, tag o parole chiave che è possibile associare ad un item. Se gli item fossero dei film, gli attributi potrebbero essere i generi, il regista, l'anno di uscita e/o gli attori. Nel caso dei testi è possibile calcolare lo score TF-IDF delle parole e utilizzare le parole con score più alto come attributi dei documenti. Nelle immagini è possibile utilizzare dei tag che ne descrivano il contenuto, estraibili automaticamente con algoritmi di machine learning.
Come descritto precedentemente, se la feature è presente nell'item, allora viene contrassegnata con , altrimenti con . Una volta fissati gli attributi è possibile rappresentare un item come un vettore. Per fissare ciò possiamo definire una funzione di rappresentazione che trasformi gli item in profili (vettori): Dove è il numero di attributi scelti.
2.3 Profilo di un utente
Partendo dalle valutazioni già effettuate dall'utente su altri item, occorre aggregare in qualche modo le valutazioni che riguardano item che condividono la stessa proprietà. La funzione di aggregazione più semplice è la media delle valutazioni.
2.3.1 Caso binario
Poniamoci nel caso binario in cui l'elemento della matrice è asserito con 1 se è stato valutato positivamente. Supponiamo che vi siano item e che gli attributi discriminanti siano . Possiamo computare il profilo dell'utente attraverso la media come segue: Dove è il profilo dell'item . Così facendo otterremo un vettore di dimensione , ovvero il profilo dell'utente. Vediamo un esempio:

Il profilo dell'utente verrà calcolato secondo la formula, per cui:
2.3.2 Caso reale
Quando la matrice di utilità non è binaria, ha senso normalizzare gli elementi della matrice di utilità per il loro valore medio. In questo modo, le valutazioni al di sotto della media avranno un punteggio negativo, mentre valutazioni sopra la media avranno un punteggio positivo. Questo metodo si adatta inoltre in base agli utenti: utenti più critici avranno medie più basse e rating bassi ma sopra la media avranno comunque un punteggio positivo (simmetricamente per utenti più gentili).
Definiamo preventivamente la media delle valutazioni dell'utente supponendo che gli item non ancora valutati abbiano valore 0 nella matrice di utilità:
Dopodiché possiamo costruire il profilo dell'utente come segue:
2.4 Similarità tra profili
Per calcolare la similarità tra profili è possibile utilizzare qualsiasi misura di similarità tra vettori. La misura più utilizzata è la similarità del coseno, che equivale al coseno dell'angolo formato dai due vettori. Dati due vettori di elementi e , la similarità del coseno è definita come: A differenza della similarità basata sulla distanza euclidea, la similarità del coseno tiene conto solo della differenza di direzione dei vettori e non degli specifici valori. Il codominio della funzione va da -1 (vettori antiparalleli) ad 1 (vettori paralleli).
2.5 Vantaggi e svantaggi
I sistemi Content-Based non richiedono confronti con altri utenti, sono facili da interpretare e promuovono gli item non popolari. Tuttavia, individuare le proprietà adatte per costruire i profili degli item può essere difficile e risulta impossibile eseguire delle previsioni su nuovi utenti che non hanno ancora valutato alcun item. Allo stesso modo, risulta impossibile eseguire predizioni su item che contengono proprietà non valutate dall'utente. Un altro difetto marcato è la overspecialization: si tende a consigliare solo oggetti simili tra loro, senza proporre all'utente nuove scelte.
2.6 Baseline
Un famoso approccio al problema della raccomandazione di item per un nuovo utente che non ha effettuato nessuna valutazione, consiste nel calcolare la baseline . La baseline rappresenta la media tra il grado medio di preferenza di tutti gli utenti, così da poter raccomandare al nuovo utente degli item che piacciono globalmente. Supponendo vi siano utenti, allora definiamo
3. Sistemi Collaborative Filtering
3.1 User-User collaborative filtering
L'idea principale dietro ai Collaborative Filters è la seguente: gli item da suggerire all'utente sono quelli valutati in maniera positiva da utenti simili ad . Tale sistema è incentrato maggiormente sul comportamento degli utenti piuttosto che sugli item.
3.1.1 Schema generale
Ipotizziamo di voler predire la valutazione dell'utente rispetto ad un item non ancora valutato. Il primo step effettuato dai Collaborative Filters è quello di individuare gli utenti più simili ad che hanno valutato l'item . Dopodiché si calcola la media delle valutazioni degli utenti sull'item , pesata in base allo score di similarità tra ciascuno degli utenti ed . Il valore ottenuto da tale media pesata è il rating predetto per l'utente sull'item .
3.1.2 Similarità tra utenti
Il profilo dell'utente in questo caso è rappresentato dalla corrispondente riga nella matrice di utilità, dove alle entry vuote viene associato il valore 0. Per calcolare la similarità tra utenti è possibile utilizzare nuovamente la similarità del coseno o, in alternativa, il coefficiente di Pearson.
Siano e due vettori, il coefficiente di Pearson corrisponde esattamente alla similarità del coseno calcolata sui vettori ridotti del loro valore medio .
Applicare la similarità del coseno direttamente sulle righe della matrice introdurrebbe un bias, dal momento in cui il valore 0 non corrisponde ad una valutazione negativa, bensì neutra. Occorre quindi normalizzare, ovvero centrare i valori di rating rispetto al valore 0, in modo che rating bassi risultino negativi e rating alti positivi. Ciò può essere ottenuto sottraendo il rating medio dell'utente a tutte le valutazioni che ha effettuato.
Esempio: ipotizziamo di avere la seguente matrice sparsa di utilità. Ipotizziamo di voler stimare la valutazione dell'utente 4 rispetto all'item 4. Consideriamo gli utenti che hanno già valutato l'item 4, che risultano essere gli utenti 2,3 e 5.
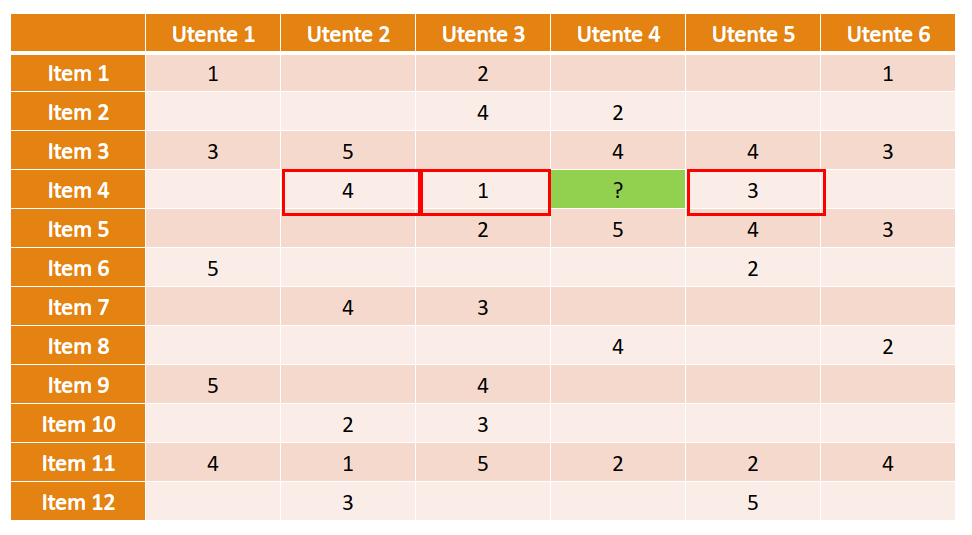
Normalizziamo i profili degli utenti 2, 3, 4 e 5 sottraendo la media degli item valutati a tutte le valutazioni e poniamo a 0 (valutazione neutra) tutti gli item non valutati.
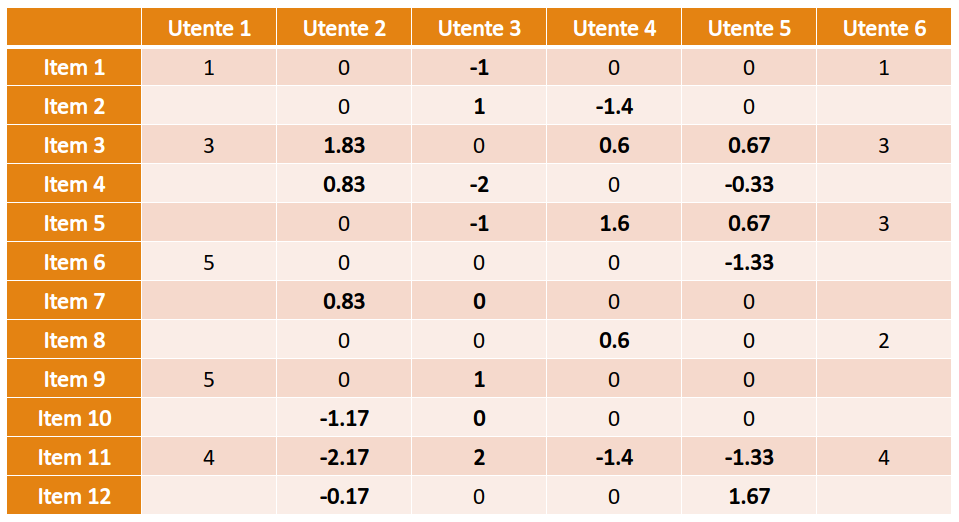
Calcoliamo la similarità del coseno tra l'utente 4 e gli utenti 2,3 e 5 e, supponendo che , otteniamo che i due utenti più simili sono 2 (con 0.47) e 5 (con 0.46). Calcoliamo la media pesata dei rating di 2 e 5 sull'item 4, ovvero la predizione della valutazione dell'utente 4 rispetto all'item 4:
3.1.3 Similarità nel caso binario
Supponiamo che la matrice di utilità sia binaria e che ogni elemento indichi se all'utente piace o meno un determinato item. Nel caso binario è possibile rappresentare il profilo dell'utente come un insieme di item piaciuti. Data la notazione insiemistica, è possibile misurare la similarità tra utenti attraverso la similarità di Jaccard (complementare della distanza di Jaccard): Tale metrica misura l'intersezione dei due insiemi, ovvero gli item che piacciono ad ambo gli utenti, rispetto all'unione dei due insiemi, ovvero la totalità di item valutati da entrambi gli utenti (fattore di normalizzazione). È compresa tra 0 ed 1, dove la massima similarità è 1 ed indica due utenti a cui piacciono esattamente gli stessi item.
3.2 Item-Item collaborative filtering
Si consideri l'utente ed un item non valutato da . Si consideri come profilo dell'item la colonna -esima della matrice di utilità, normalizzata sottraendo la media delle proprie valutazioni. Si trovino gli item più simili ad e valutati dall'utente , utilizzando la distanza del coseno (o il coefficiente di Pearson). A questo punto si stimi la valutazione dell'utente rispetto all'item attraverso la media dei rating dati dall'utente agli item più simili ad , pesata con lo score di similarità. Il risultato sarà la valutazione predetta.
Tale schema differisce dai sistemi content-based in quanto il profilo dell'item non è costruito attraverso gli attributi dell'item stesso, bensì attraverso le valutazioni degli utenti nella matrice di utilità. Nella pratica, i sistemi Item-Item funzionano meglio poiché gli utenti tendono ad avere preferenze diverse.
3.3 Approccio comune
Supponiamo di voler predire la valutazione dell'utente rispetto all'item . Indichiamo per brevità con la similarità tra gli item e . Partiamo da una stima baseline per calcolata come segue Dove è la media generale di tutti i film, rappresenta la deviazione delle valutazioni dell'utente dalla media e rappresenta la deviazione del rating per l'oggetto rispetto alla media Alla valutazione baseline si aggiunge lo score ottenuto dalla tecnica collaborative filtering:
3.4 Confronto tra collaborative filters
Le due strategie comportano un trade-off tra efficienza ed accuratezza. Lo schema basato sulla similarità degli item è più informativo e permette di ottenere predizioni più affidabili. Questo poiché vi sono generalmente più item che utenti nella matrice di utilità ed è più facile trovare item dello stesso genere che utenti a cui piacciono solo item di un certo genere (il profilo di un utente è quasi univoco).
Lo schema basato sulla similarità tra utenti è tuttavia più efficiente se vogliamo predire tutti i rating dell'utente . Questo è conseguenza del fatto che una riga della matrice di utilità ha molte entry vuote. Utilizzando lo schema basato sugli utenti è sufficiente individuare l'insieme degli utenti simili ad per stimare il rating di vari item non valutati da . Nel sistema item-item, per ogni item non valutato è necessario ri-calcolare la similarità.
3.5 Vantaggi e svantaggi
I sistemi Collaborative Filtering lavorano con tutti gli utenti, anche aventi proprietà diverse. Non è necessaria una selezione di proprietà o feature sugli item. Tuttavia, non è possibile eseguire predizioni su nuovi utenti o riguardanti nuovi item. Nella pratica, i sistemi di raccomandazione sono ibridi, ovvero una combinazione tra le due tecniche.
4. Singular Value Decomposition (SVD)
4.1 Dimensionality reduction
I sistemi di raccomandazione lavorano solitamente su una matrice di utilità di grandi dimensioni, con un elevato numero di utenti ed item. In un contesto in cui subentrano i Big Data, i problemi principali sono:
- L'efficienza: operazioni svolte su matrici e vettori di grandi dimensioni.
- Problema della dimensionalità: in uno spazio ad elevate dimensioni, i punti tendono ad essere tutti equidistanti gli uni dagli altri, rendendo complesso il calcolo della similarità.
Occorre quindi adottare delle tecniche di dimensionality reduction (riduzione della dimensionalità), che permettono ai sistemi di raccomandazione di operare con matrici e vettori più piccoli.
4.2 Clustering di item e/o utenti
Una tecnica naive per provare a ridurre la dimensionalità è il clustering. Se due o più item hanno caratteristiche simili, allora potrebbero far parte di uno stesso cluster. L'idea è quella di disporre i cluster sulle colonne della matrice di utilità, anziché gli item.
L'entry si riferirà alla valutazione dell'utente rispetto al cluster , dove la valutazione del cluster è data dalla media delle valutazioni dell'utente sugli elementi del cluster. Si può effettuare analogamente il clustering di utenti e sostituire le righe con cluster di utenti. I due metodi di riduzione possono essere adottati in contemporanea. Tale tecnica è utile ma utilizzabile solo in casi particolari e, inoltre, richiede l'esecuzione di algoritmi di clustering su grosse moli di dati.
4.3 Decomposizione di matrici
Supponiamo che esista un insieme relativamente piccolo di feature di item ed utenti che determinano la valutazione della maggior parte di utenti per la maggior parte di item. Queste feature, riprendendo l'idea del clustering, sosno rappresentative di intere categorie o gruppi di feature.
L'idea è quella di utilizzare delle tecniche di decomposizione o fattorizzazione di matrici (che esprimono una matrice come prodotto di due o più matrici). Le tecniche di fattorizzazione permettono di fattorizzare una matrice :
- Come prodotto di due matrici di dimensione, rispettivamente, .
- Come prodotto di tre matrici di dimensione, rispettivamente,
Alcune scomposizioni d'esempio sono la decomposizione LU, la decomposizione UV, la singular value decomposition (SVD), etc.
4.4 Singular Value Decomposition
La SVD è una tecnica di decomposizione spettrale di una matrice di dimensione nel prodotto di tre matrici: Dove:
- è una matrice unitaria di dimensione
- è una matrice diagonale di dimensione , i cui elementi sulla diagonale sono non negativi
- è una matrice unitaria di dimensione
Ricordiamo che una matrice è unitaria se e solo se .
4.4.1 Proprietà della SVD
- La decomposizione esiste sempre.
- Gli elementi di vengono chiamati valori singolari di .
- Il numero di valori singolari non nulli (diagonale di ) corrisponde al rango di .
- Le colonne della matrice sono chiamate vettori singolari di sinistra.
- Le colonne della matrice sono chiamate vettori singolari di destra.
- I vettori singolari di sinistra di sono gli autovettori della matrice
- I vettori singolari di destra di sono gli autovettori della matrice
- I valori singolari di non nulli sono le radici quadrate degli autovalori non nulli di ed
Trovare la decomposizione SVD di una matrice consiste nel trovare autovettori ed autovalori delle matrici ed .
4.4.2 Interpretazione geometrica
Sia una matrice . Nel piano consideriamo un cerchio di raggio unitario con i due vettori unitari canonici (basi standard). La SVD ruota e trasforma il cerchio in un ellisse i cui semiassi hanno lunghezze pari ai valori singolari non nulli di .
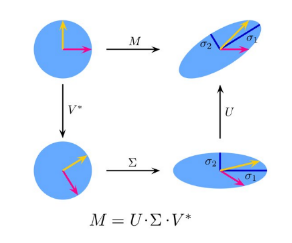
4.4.3 SVD nei sistemi di raccomandazione
Nell'ambito dei sistemi di raccomandazione SVD può essere applicata per velocizzare il sistema, trasformando la matrice di utilità nel prodotto di matrici più sottili, su cui risulti più semplice effettuare la predizione. Sia la matrice di utilità formata da utenti ed item. Allo spazio formato da utenti ed item, la decomposizione SVD affianca un secondo spazio chiamato spazio delle categorie.
La decomposizione SVD permette di mappare dati dallo spazio degli utenti e degli item allo spazio delle categorie e viceversa. Riprendendo la definizione della scomposizione: Dove in questo caso:
- U è una matrice unitaria formata da utenti ed categorie
- è una matrice diagonale di dimensioni , con elementi della diagonale non negativi
- è una matrice unitaria formata da item ed categorie.
4.4.4 Calcolo delle predizioni con SVD
Usando SVD possiamo calcolare le predizioni di un utente per tutti gli item mediante un prodotto di matrici.
- Sia un utente ed il vettore di lunghezza contenente i rating correnti su tutti gli item (se il rating per un item non è conosciuto poniamo 0).
- Si moltiplica per , il che equivale a mappare i rating correnti dallo spazio originale a quello delle categorie. Sia .
- Si moltiplica per , il che equivale a ri-mappare i valori dallo spazio delle categorie allo spazio originale. Sia
- Il vettore contiene le predizioni dei rating di su tutti gli item.
4.4.5 Esempio
Consideriamo un nuovo utente : ha visto solo il film Matrix, valutandolo 4 stelle su 5. Supponiamo di avere la matrice di utilità in figura. Il profilo dell'utente è . Vogliamo predire il rating di sugli altri film.
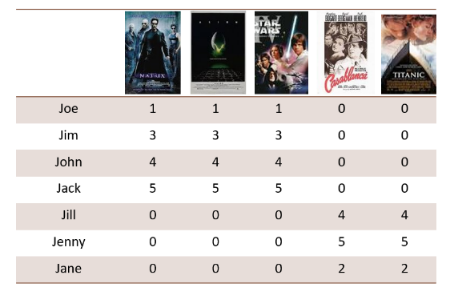
Proseguiamo calcolando il rango della matrice attraverso uno dei metodi di calcolo del rango (i.e. criterio dei minori, teorema di Kronecker o degli orlati, eliminazione gaussiana). Il rango della matrice risulta essere 2. Quindi lo spazio delle categorie è formato da due sole categorie (in questo caso Fantascienza e Amore). Calcoliamo gli autovettori ed autovalori delle matrici ed e costruiamo la decomposizione:
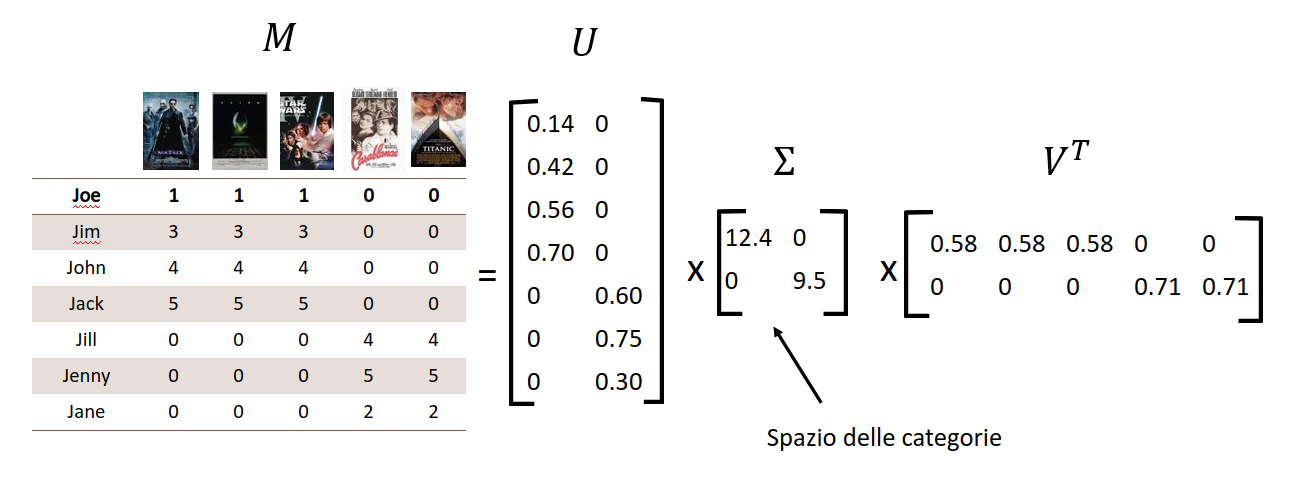
Mappiamo adesso nello spazio delle categorie attraverso il prodotto :
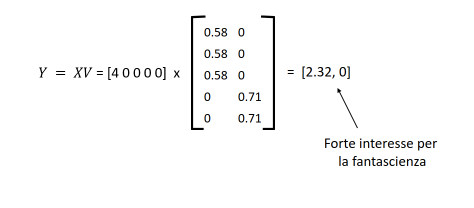
E ri-mappiamo nello spazio dei film attraverso il prodotto :

Con il seguente risultato:

5. Valutazione dei risultati
Un sistema di raccomandazione può essere visto come un classificatore o un predittore. Se conosciamo i valori reali di rating, possiamo valutare la qualità del sistema confrontando i valori predetti con quelli reali. Nei casi in cui la matrice di utilità è binaria (like / not like), o nel caso in cui non è rilevante predire il valore esatto di rating ma semplicemente se è positivo o negativo, è possibile utilizzare le tecniche standard viste per la classificazione (precision, recall, accuracy, TPR, FPR, etc.).
Se siamo invece interessati a predire il valore esatto, possiamo utilizzare tecniche standard per valutare la qualità di un predittore. La misura più utilizzata è il Root Mean Square Error (RMSE): Dove è il vettore dei rating predetti ed è il vettore dei rating reali.
Reti neurali
1. Introduzione
1.1 Reti neurali biologiche
I neuroni sono le più importanti cellule del sistema nervoso. Le connessioni sinaptiche (o sinapsi) agiscono come porte di collegamento per il passaggio dell'informazione tra neuroni. I dendriti sono fibre minori che si ramificano a partire dal corpo cellulare del neurone (detto soma). Attraverso le sinapsi, i dendriti raccolgono input da neuroni afferenti e li propagano verso il soma. L'assone è la fibra principale che parte dal soma e si allontana da esso per portare ad altri neuroni (anche distanti) l'output.
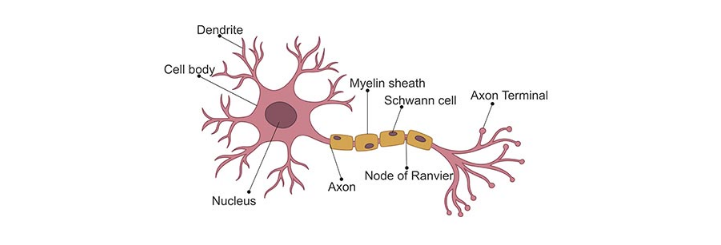
Il passaggio delle informazioni attraverso le sinapsi avviene con processi elettro-chimici: il neurone presinaptico libera delle sostanze, chiamate neurotrasmettitori, che attraversano il breve gap sinaptico e sono captati da appositi recettori, detti canali ionici, sulla membrana del neurone postsinaptico. L'ingresso di ioni attraverso i canali ionici determina la formazione di una differenza di potenziale tra il corpo del neurone postsinaptico e l'esterno. Quando questo potenziale supera una certa soglia, detta di attivazione, si produce uno spike o impulso: il neurone propaga un breve segnale elettrico detto potenziale d'azione lungo il proprio assone: questo potenziale determina il rilascio di neurotrasmettitori dalle sinapsi dell'assone.
Il reweighting delle sinapsi, ovvero la modifica della loro efficacia di trasmissione, è direttamente collegato ai processi di apprendimento e memoria in accordo con la regola di Hebb.
Hebbian Rule: se due neuroni, tra loro connessi da una o più sinapsi, sono ripetutamente attivati simultaneamente allora le sinapsi che li connettono sono rinforzate.
Il cervello umano contiene circa 100 miliardi di neuroni, ciascuno dei quali connesso con circa altri 1000 neuroni ( sinapsi). La corteccia celebrale (sede delle funzioni nobili del cervello umano) è uno strato laminare continuo di 2-4 mm, una sorta di lenzuolo che avvolge il nostro cervello formando numerose circonvoluzioni per acquisire maggiore superficie. Sebbene i neuroni siano disposti in modo ordinato in livelli consecutivi, l'intreccio di dendriti e assoni ricorda una foresta fitta ed impenetrabile.
1.2 Reti neurali artificiali
Il primo modello di neurone artificiale fu progettato da McCulloch e Pitts: gli input e gli output erano binari ed erano in grado di eseguire delle computazioni logiche.
Un neurone artificiale moderno prende in ingresso input , pesati rispettivamente con pesi che rappresentano l'efficacia delle connessioni sinaptiche dei dendriti. Tali valori varieranno durante il processo di apprendimento. Esiste un ulteriore peso, detto costante di bias, che si considera collegato ad un input fittizio con valore costante 1, questo peso è utile per tarare il punto di lavoro ottimale del neurone.
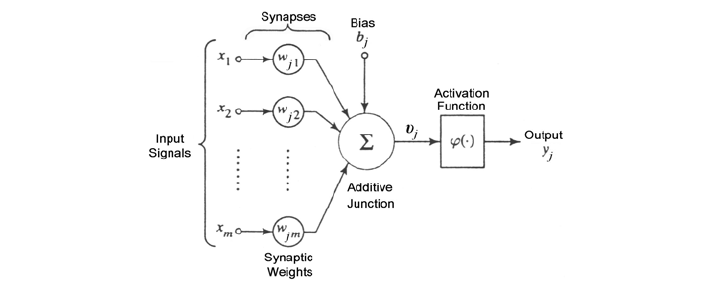
Il neurone somma i prodotti tra gli input ed i corrispettivi pesi (compresa la costante di bias) e produce un valore . Dopodiché, sulla base di una funzione di attivazione a cui viene passato il valore , produce un valore di output.
1.2.1 Layer
Le reti neurali sono composte da gruppi di neuroni artificiali organizzati in livelli o layer. Tipicamente sono presenti un layer di input, un layer di output, ed uno o più layer intermedi o nascosti (hidden). Ogni layer contiene uno o più neuroni.
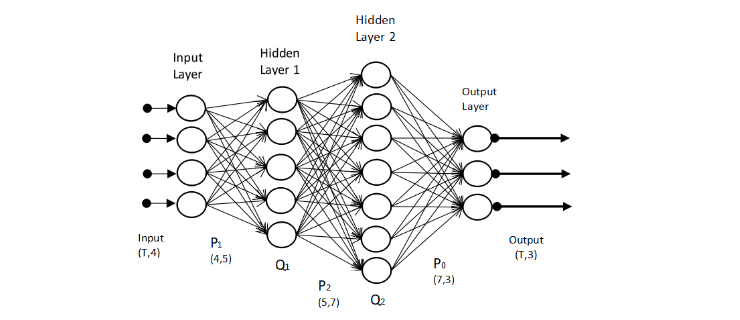
Il layer di input è costituito da un vettore di valori . Gli hidden layer sono costituiti da uno o più nodi che prendono in input uno o più valori provenienti dal layer precedente. Ogni nodo dell'hidden layer produrrà un output che verrà passato ad uno o più nodi del layer successivo. Il layer di output è costituito da uno o più nodi che restituiscono in output un valore. Il termine deep neural network indica una rete formata da molti layer nascosti.
1.2.2 Tensori
Nel contesto delle reti neurali, un tensore è un array -dimensionale, ovvero una generalizzazione di un vettore o di una matrice. Nel modello più generale di rete neurale sia l'input che l'output di un nodo della rete può essere un tensore. I nodi di un layer possono essere organizzati e disposti a formare una matrice (come nelle convolutional networks) o un tensore. Nel primo caso ritroviamo il tensore al livello dei dati, mentre nel secondo lo ritroviamo come disposizione dei nodi della rete.
1.2.3 Connessioni tra layer
Una rete neurale in cui ogni nodo di un certo layer riceve tutti gli output del layer precedente è detta densa. In questo caso si parla di layer totalmente connessi. Altre tipologie di connessioni tra layer sono possibili:
- Connessione random: fissato , ogni nodo riceve output solamente da nodi (generalmente casuali) del precedente layer.
- Connessione pooled: i nodi di un layer sono partizionati in cluster. Il layer successivo, chiamato pooled layer, sarà formato da nodi, uno per ogni cluster. Il nodo associato al cluster riceverà tutti e soli gli output dei nodi del layer precedente appartenenti al cluster .
- Connessione convolutional: i nodi di ogni layer sono visti come se fossero disposti su una griglia. Il nodo di coordinate riceve tutti e soli gli input dei nodi del layer precedente che si trovano in una regione piccola della griglia intorno al punto (vediamo una immagine che rappresenti cosa si intende per convoluzione).
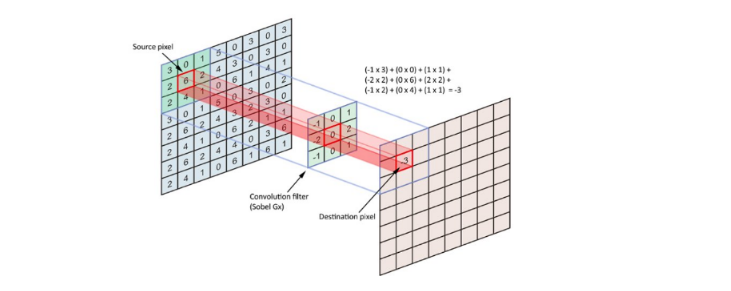
1.3 Explanable AI
La rete neurale si presenta come un modello black-box: un osservatore esterno vede l'output prodotto dal modello a partire da un input, ma il modello non è in grado di giustificare il risultato ottenuto, ovvero non è in grado di spiegare il procedimento logico per cui si arriva a produrre quel risultato. Il termine Explanable AI indica una serie di tecniche a supporto di modelli di intelligenza artificiale per far sì che un risultato prodotto da tali modelli possa essere compreso da un essere umano. Tali tecniche sono molto importanti in ambito medico, nella guida autonoma, nella computer vision, etc.
1.4 Progettare una rete neurale
La costruzione di una rete neurale è fondamentale per ottenere un modello di machine learning in grado di classificare o predire accuratamente. Per prima cosa bisogna definire la struttura della rete:
- Quanti hidden layer definire?
- Quanti nodi deve contenere ciascun layer?
- Come connettere i nodi di layer consecutivi?
- Quale funzione di attivazione scegliere per ogni layer?
Una volta definita la struttura, il modello deve essere addestrato su un training set al fine di trovare i valori ottimali dei pesi degli input ricevuti da ogni nodo della rete neurale in ogni layer. Per fare ciò occorre definire una funzione di costo globale , detta funzione loss, e trovare i pesi che la minimizzino. Le due ulteriori domande da porsi sono:
- Come deve essere organizzato il training set? Da quanti elementi?
- Quale funzione loss scegliere?
La progettazione di una rete neurale è per lo più uno studio empirico, fatto di tentativi. Le linee guida per la progettazione sono le seguenti:
- Una rete neurale con meno layer richiede tempi di addestramento ed esecuzione minori.
- Una rete neurale con più layer permette di risolvere problemi decisionali più complessi.
- Troppi layer producono un modello troppo complesso con un concreto rischio di overfitting.
- Tre layer sono spesso buoni nella pratica.
- Definire molti nodi in un hidden layer permette di identificare pattern più complessi nei dati.
- Per prevenire l'overfitting è conveniente partire da un basso numero di nodi ed aumentarlo gradualmente, monitorando le performance del modello.
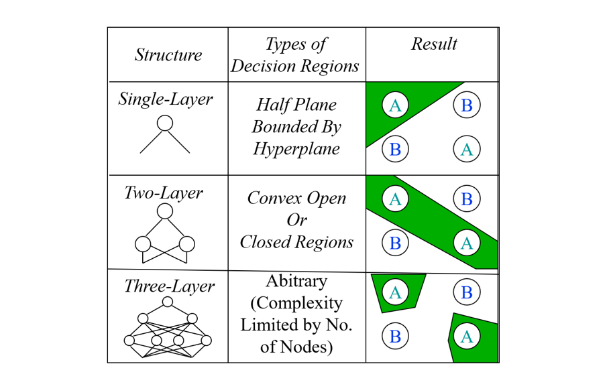
2. Funzioni di attivazione
2.1 Definizione formale
Sia il vettore dei valori ricevuti da un nodo, il vettore dei pesi e la costante di bias. La funzione di attivazione di un nodo è la funzione che determina la risposta prodotta a partire da: Tutti i nodi di un layer hanno la stessa funzione di attivazione.

2.2 Proprietà desiderate
La scelta della funzione di attivazione si lega al metodo scelto per ottimizzare i pesi della rete basato sulla minimizzazione della funzione loss. Il metodo di minimizzazione più popolare è quello della discesa del gradiente (gradient descent). Affinché il gradient descend lavori al meglio, la funzione di attivazione deve avere delle proprietà desiderate:
- La funzione deve essere continua e differenziabile in ogni punto (o quasi).
- La derivata della funzione non deve saturare, ovvero tendere a zero nel proprio dominio: questo potrebbe portare ad uno stallo nel processo di ricerca dei pesi ottimali.
- La derivata della funzione non deve esplodere, ovvero tendere all'infinito nel proprio dominio: questo potrebbe portare instabilità numerica nel processo di ricerca dei pesi ottimali.
2.3 Unit step function
La più semplice funzione di attivazione è la funzione step, chiamata anche heaviside step o unit step function. Il nodo che usa la funzione step restituisce valori binari e viene per questo chiamato percettrone. La funzione è definita come segue:
La derivata della funzione unit step function è notoriamente la funzione Delta di Dirac . Quest'ultima satura a 0 per ed esplode ad quando , per cui non rispetta delle proprietà desiderate e non è una buona scelta per una deep neural network.
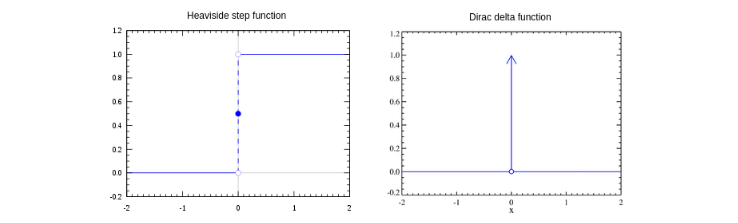
Può essere utilizzata per costruire un classificatore discriminativo binario o multi-classe. Il Perceptron è un esempio di classificatore binario, con un solo nodo nell'output layer che restituisce 1 se un oggetto è di una classe, 0 se è dell'altra. Per ottenere un classificatore discriminativo multi-classe occorre creare nell'output layer un percettrone per ogni classe da riconoscere. La rete neurale produrrà in output un vettore binario con un solo valore pari ad 1, che determinerà la classe finale, e tutti gli altri posti a 0. Uno o più hidden layer sono necessari per catturare pattern specifici di ciascuna classe al fine di guidare l'output layer ad identificare la classe corretta.
2.4 Funzione logistica
La funzione logistica, affrontata nel capitolo sulla predizione, appartiene alla classe delle funzioni sigmoidee, aventi cioé una curva a forma di . La definizione è la seguente: La funzione assume valore per ; quando la funzione , mentre quando la funzione .
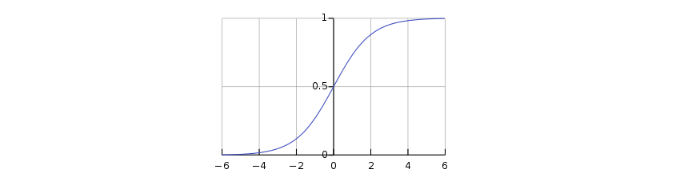
Dal grafico osserviamo la somiglianza con la funzione unit-step. La differenza chiave sta nell'approccio della funzione tendendo allo zero: l'andamento è graduale anziché diretto. Dato un vettore di valori , la funzione logistica è applicata su ognuna delle componenti: Se indichiamo con , allora la derivata della funzione logistica è: Allontanandosi dal punto in ambo le direzioni, la derivata tende a 0 e quindi la funzione tende a saturare (prop. 1). A differenza della unit-step function, la funzione logistica restituisce valori tra 0 ed 1 (prop. 2). Nel contesto della classificazione ciò implica che la funzione logistica può essere utilizzata nel layer di output per restituire la probabilità di appartenenza a ciascuna classe.
2.5 Tangente iperbolica
Anche la tangente iperbolica appartiene alla classe delle funzioni sigmoidee ed è definita come:
La tangente iperbolica risulta legata alla funzione logistica dalla seguente relazione:
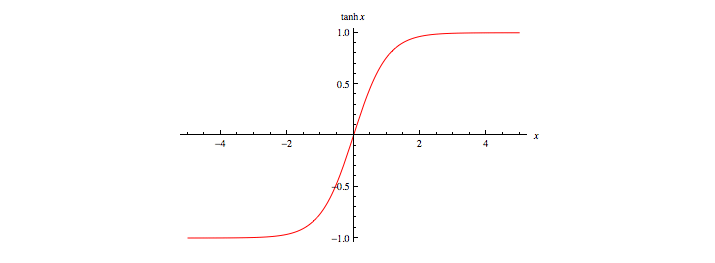
In altre parole, la tangente iperbolica è una versione scalata e traslata della funzione logistica. Essa ha valori compresi tra -1 ed 1 ed è simmetrica rispetto all'asse . Gode delle stesse proprietà enunciate per la funzione logistica.
2.6 Funzione softmax
A differenza delle funzioni sigmoidee, la funzione softmax non opera sulla singola componente del vettore, ma sull'intero vettore. Sia un vettore di valori, la funzione softmax è definita come dove il generico è calcolato come segue: La funzione ha valori in come la funzione logistica. La somma dei valori calcolati su ogni componente del vettore è 1, dunque è una distribuzione di probabilità. Grazie all'esponenziale, le componenti del vettore con valori più alti ricevono valori molto più alti rispetto alle altre. In particolare se c'è una componente con un valore significativamente più alto rispetto a tutti gli altri, a questa componente corrisponderà un valore vicino ad 1, mentre alle restanti un valore prossimo allo 0. La softmax ha problemi di saturazione, che possono essere aggirati utilizzando come funzione costo l'entropia incrociata.
Il denominatore della funzione softmax coinvolge una somma di esponenziazioni. Quando i valori variano in un range molto ampio, le loro esponenziazioni finiscono per variare in un range esponenzialmente più ampio, che coinvolge valori molto piccoli e molto grandi. Sommare valori molto piccoli e molto grandi può portare a problemi di accuratezza nel calcolo svolto da una macchina.
Osserviamo che per una qualsiasi costante : Se fissiamo , allora ogni esponente avrà come potenza un valore e quindi le somme avranno addendi compresi nell'intervallo [0, 1], il che porta ad un calcolo più accurato.
2.7 Rectified Linear Unit (ReLU)
La funzione ReLU prende spunto dai raddrizzatori a singola semionda (half-wave rectifiers) usati in elettronica per trasformare un segnale alternato in un segnale unidirezionale (sempre positivo o sempre negativo) facendo passare solo semionde positive. È formalmente definita come segue: Rappresentabile con il seguente grafico:
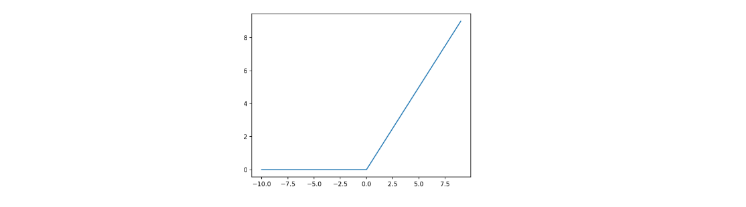
La funzione ReLU non satura mai per valori di positivi. Nella pratica, le reti neurali che utilizzano ReLU offrono uno speed-up significativo nella fase di training rispetto alle funzioni sigmoidee. Sia il calcolo della funzione che della sua derivata sono molto semplici e veloci da effettuare poiché non è richiesta l'esponenziazione. ReLU soffre di problemi di saturazione della sua derivata quando è negativo.
2.8 Exponential Linear Unit (ELU)
Un miglioramento per ReLU che attenua il problema della saturazione per consiste nel definire una variante chiamata ELU (Exponential Linear Unit), definita come segue: Dove è un iper-parametro tenuto fisso durante il learning dei pesi. Il processo di learning viene ripetuto con diversi valori di per trovare il valore che permette di ottenere performance migliori.
3. Funzioni Loss
La loss function, o funzione costo, è quella funzione utilizzata nel processo di learning dei pesi del modello. Essa quantifica la differenza tra le predizioni di un modello e i valori corretti di output osservati nel training set, quindi l'errore medio di predizione tra valori predetti e valori reali. I pesi ottimali sono quelli che minimizzano la funzione loss. Distinguiamo due tipologie di funzioni loss in base al problema che affronta la rete neurale:
- Regression loss nei problemi di regressione, da in output uno scalare o un vettore di valori reali
- Classification loss nei problemi di classificazione, da in output una distribuzione di probabilità, con valori che indicano la probabilità di appartenenza ad una classe.
3.1 Regression loss
Sia l'input, l'output reale ed il valore predetto dalla rete neurale. Le prime due regression loss function più comuni sono la squared error loss: e la Huber loss: dove è una costante. La Huber loss è in parte definita come la squared error loss (per valori minori di ). Supponendo , osserviamo le due funzioni a confronto in funzione al valore ():
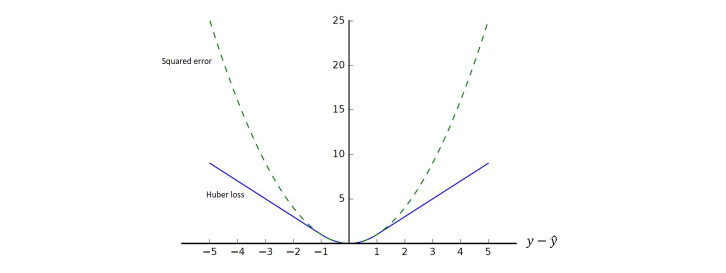
La Huber loss penalizza di meno le differenze tra i valori reali e quelli predetti, mentre la squared error loss tende all'infinito anche con errori relativamente piccoli. La variante Huber loss protegge il processo di learning nel caso di outlier, dove la squared error segnalerebbe un errore molto grande.
3.1.1 Mean Squared Error (MSE)
Le funzioni squared error ed Huber loss funzionano per un solo dato. Nel caso volessimo calcolare l'errore su un insieme di dati su cui è stata effettuata una predizione, dovremmo affidarci ad altri metodi.
Sia il training set e l'insieme di coppie formate dai valori di input e dai rispettivi output predetti dalla rete. Definiamo il Mean Squared Error come la misura dell'errore quadratico medio: La radice quadrata del MSE è definita Root Mean Square Error (RMSE). Nella pratica è preferibile il MSE perché il calcolo della derivata (ai fini dell'utilizzo del gradient descent) è più semplice. A causa del termine al quadrato, il MSE è molto sensibile agli outliers. Pochi outlier possono incrementare di molto il valore MSE, compromettendo il learning. Per attenuare questo effetto, conviene calcolare l'errore medio utilizzando la Huber Loss.
3.1.2 Regression loss con vettori
Nel caso in cui l'output è un vettore di valori anziché uno scalare, si sostituisce nel calcolo della squared loss, della Huber loss e del MSE la norma della differenza tra i vettori reale e predetto al posto della differenza tra i valori scalari.
3.2 Classification loss
Poniamoci in un generale problema di classificazione con classi . Supponiamo di avere un training set dove è il vettore degli input e è una distribuzione di probabilità. La componente del vettore indica la probabilità che appartenga alla classe .
Supponiamo che la rete neurale sia progettata, ad esempio attraverso una softmax, per produrre in output una distribuzione di probabilità , dove indica la probabilità predetta dal modello che sia di classe . Le funzioni di classification loss quantificano la distanza tra le distribuzioni di probabilità e .
3.2.1 Entropia
Supponiamo di avere un alfabeto di simboli. Si vuole trasmettere un messaggio utilizzando questi simboli attraverso un canale di informazione. Sia una distribuzione di probabilità. Supponiamo che in ogni punto del messaggio la probabilità di osservare l'-esimo simbolo sia .
Il teorema di Shannon afferma che, in un sistema di codifica ottimale, il numero medio di bit per simbolo necessari per codificare il messaggio è dato dall'entropia : Il termine indica il numero di bit necessari a rappresentare l'-esimo simbolo usando lo schema di codifica ottimale. Qualunque altro schema utilizza in media più bit, dunque è sub-ottimale.
3.2.2 Entropia incrociata
Nella teoria dell'informazione, l'entropia incrociata (o cross-entropy) tra due distribuzioni di probabilità e , relative allo stesso insieme di eventi, misura il numero medio di bit necessari ad identificare un evento estratto dall'insieme nel caso sia utilizzato uno schema alternativo anziché la vera distribuzione .
Supponiamo di cambiare lo schema di codifica, usando una diversa distribuzione di probabilità . Con questo nuovo schema occorrono bit per rappresentare l'-esimo simbolo. Quanti bit per simbolo occorrono in media se usiamo questo schema di codifica sub-ottimale? Dalla definizione di entropia incrociata possiamo calcolarlo come segue:
3.2.3 Divergenza di Kullback-Leibler
In generale sappiamo che poiché è sub-ottimale, mentre è ottimale. La differenza tra e , chiamata Divergenza di Kullback-Leibler (KL), misura il numero medio di bit in più che occorrono per ogni simbolo: Minimizzare la divergenza di equivale a minimizzare l'entropia incrociata. Nella pratica si utilizza l'entropia incrociata come funzione loss. Essa è la più comune funzione di classification loss ed è spesso accoppiata (es. in TensorFlow) con la funzione di attivazione softmax in un'unica funzione numericamente più stabile, la cui derivata è semplice da calcolare.
3.2.4 Binary Cross-Entropy Loss
Come abbiamo già detto, la cross-entropy può essere utilizzata per definire una funzione loss. Poniamoci nel caso binario in cui le sole due classi di appartenenza sono . Sia la reale probabilità che la -esima tupla appartenga alla classe 1. Sia la probabilità stimata dall'algoritmo che la -esima tupla appartenga alla classe 1.
Utilizziamo una funzione di attivazione che dia in output delle probabilità, come la softmax. Data una tupla , la softmax ci comunicherà che con probabilità la tupla apparterrà alla classe 1, mentre con probabilità la tupla apparterrà alla classe 0.
Avendo fissato le notazioni e è possibile utilizzare la cross-entropy per misurare la dissimilarità tra e : Utilizziamo la cross-entropy come loss function per una tupla ed ipotizziamo di voler calcolare la cross-entropy media per tutte le tuple del training set: Tale funzione loss è chiamata binary cross-entropy loss.
4. Training di una rete neurale
Il processo di training consiste nel trovare i parametri della rete (pesi) che minimizzano l'average loss (quantificato mediante la funzione di loss scelta) su un training set di dati. L'obiettivo finale è costruire un modello che garantisca un loss medio basso su tutti i possibili input. Dato l'elevato numero di parametri di una rete neurale (specialmente se deep) il rischio di overfitting è alto. Concentriamoci inizialmente sulla minimizzazione della funzione di loss sul training set.
4.1 Derivate parziali e gradiente
È possibile estendere l'idea della derivata alle funzioni multivariate. Sia una funzione ad variabili. La derivata parziale di rispetto alla componente -esima è:
Per calcolare la derivata parziale di rispetto alla componente -esima è sufficiente trattare tutte le variabili meno che la -esima come costanti e calcolare la derivata di . Le seguenti notazioni sono equivalenti:
Raggruppando le derivate parziali di una funzione multivariata rispetto ad ognuna delle sue componenti otteniamo il vettore gradiente della funzione. Supponiamo che l'input della funzione sia un vettore -dimensionale e che l'output sia invece uno scalare. Il gradiente della funzione rispetto ad è un vettore di derivate parziali:
Sia un vettore -dimensionale, le seguenti regole sono spesso utilizzate nella differenziazione di funzioni multivariate:
Similmente, per ogni matrice , abbiamo che .
4.2 Matrice jacobiana
Sia un vettore di valori reali. Sia ed . La matrice jacobiana di rispetto ad è la matrice formata dalle derivate parziali prime di ciascuna componente di rispetto a ciascuna componente di :
4.3 Metodo di discesa del gradiente
Il metodo di discesa del gradiente (gradient descent) è una tecnica atta ad individuare i punti di minimo (o di massimo) di una funzione di più variabili. Nel contesto delle reti neurali la funzione da minimizzare è la funzione loss calcolata sui parametri correnti del modello.
Partendo da un valore iniziale assunto dai parametri della funzione, il metodo iterativamente cerca la direzione di massima discesa del valore della funzione e aggiorna i valori dei parametri seguendo tale direzione. La direzione di massima discesa è quella opposta al gradiente (o alla matrice jacobiana nel caso in cui il codominio della funzione è multidimensionale).
4.3.1 Schema del metodo
Sia la funzione loss da minimizzare. Indichiamo con la matrice di parametri della rete neurale calcolato dall'algoritmo all'iterazione . La procedura generale dell'algoritmo di discesa del gradiente è la seguente:
- Per inizializzare la matrice dei pesi con valori casuali.
- Calcolare la funzione loss con i parametri ed il gradiente .
- Aggiornare la matrice dei pesi
- Passare alla iterazione successiva e ripartire dal secondo step.
Il metodo viene iterato sino a quando i valori del vettore non cambiano in maniera significativa. Analogo metodo per la matrice Jacobiana. Essendo basato su una scelta greedy, non garantisce l'individuazione di minimi assoluti, per cui può convergere ad un minimo locale. Il vettore ottenuto dopo la convergenza dell'algoritmo contiene i parametri della rete che minimizzano la funzione loss.
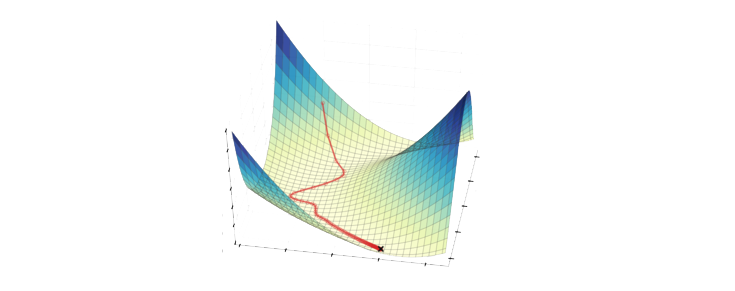
4.3.2 Learning rate
Il parametro (eta) è detto learning rate e determina la velocità con cui si desidera che il metodo converga al valore ottimale. Valori troppo bassi implicano che la convergenza richieda molte iterazioni. Dall'altra parte, valori molto alti possono causare grandi oscillazioni nei valori dei parametri della rete, impedendo di arrivare a convergenza. Un metodo per trovare il learning rate ottimale consiste nel partire da un valore alto di e ad ogni passo moltiplicare per un fattore (con ) fino ad ottenere un valore di che porti a convergenza.
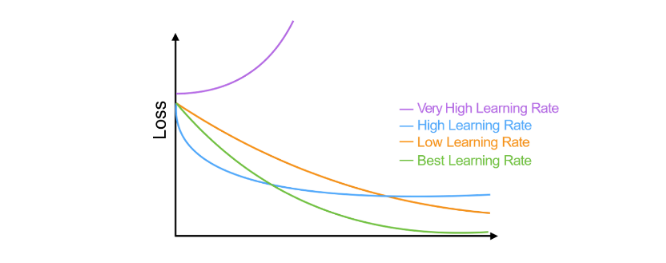
4.3.3 Inizializzazione dei pesi della rete
Per applicare il metodo di discesa del gradiente occorre partire da un valore iniziale della funzione loss, poiché quest'ultima deve essere calcolata su una rete neurale già definita con dei pesi assegnati. Si pone quindi il problema di inizializzare i pesi della rete. Intuitivamente, se vogliamo che i nodi di un layer si comportino in maniera diversa (e riconoscano feature diverse sugli input ricevuti) occorre scegliere dei pesi diversi. Vi sono due approcci:
- Scegliere casualmente pesi in seguendo una distribuzione uniforme
- Scegliere casualmente secondo una distribuzione normale
4.3.4 Stochastic gradient descent
Il metodo stochastic gradient descent è una variante della discesa del gradiente in cui, ad ogni iterazione del metodo, si lavora su un piccolo campione di dati del training set selezionato in maniera casuale. Tale variante risulta più veloce del gradient descent originale quando il training set è troppo grande.
4.3.5 Calcolo del gradiente
Una volta calcolata la funzione loss su un vettore di output, occorre calcolare il gradiente della funzione loss rispetto ai pesi della rete in quel determinato momento. Un algoritmo efficiente per il calcolo del gradiente è l'algoritmo di backpropagation, che sfrutta il concetto di grafo computazionale.
4.4 Backpropagation
4.4.1 Forward propagation
Il termine forward propagation (o forward pass) si riferisce al calcolo e all'archiviazione ordinata di variabili intermedie della rete neurale, dall'input layer all'output layer.
Per semplicità assumiamo che l'input d'esempio sia e che vi sia un solo layer nascosto nella rete, che non includa alcun termine di bias. Sia una variabile intermedia: Dove è la matrice dei pesi dell'unico hidden layer. Diamo in input tale variabile alla funzione di attivazione e otteniamo un vettore di attivazione di lunghezza : Anche la variabile è una variabile intermedia. Assumendo che l'output layer possegga una matrice di pesi , otteniamo il risultato dell'output layer e poniamolo in una variabile temporanea di lunghezza : Assumendo che la funzione loss sia e che la classe dell'esempio sia , possiamo calcolare la loss per la predizione di come segue: Dalla definizione della regolarizzazione , dato un parametro , il termine di regolarizzazione è Dove la norma di Frobenius (o norma matriciale) è semplicemente la norma applicata dopo aver concatenato la matrice in un singolo vettore. Otteniamo quindi l'ultimo termine , ovvero la loss regolarizzata: Ci riferiremo a con il nome di objective function o funzione loss regolarizzata
4.4 Grafo computazionale
Un grafo computazionale è un grafo aciclico diretto (DAG) che permette di visualizzare il flusso di dati di una rete neurale. Ogni nodo può avere due forme: un nodo quadrato indica un valore (tensore di dimensione arbitraria), mentre un nodo circolare indica una operazione. La direzione indica che il nodo mittente è operando del nodo destinatario, o che il nodo destinatario è output del nodo mittente. Visualizziamo il grafo computazionale della rete neurale descritta dalla forward propagation:
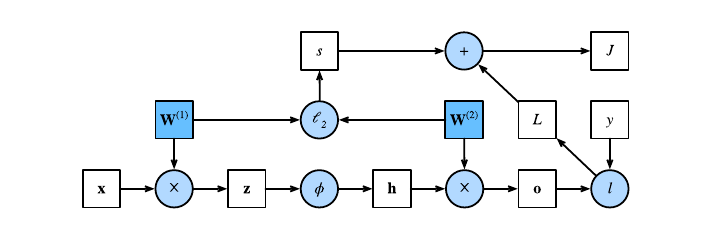
4.5 Chain rule
La regola della catena, in inglese chain rule, è una regola di derivazione che permette di calcolare la derivata di una funzione composta da due funzioni derivabili.
Supponiamo che le funzioni ed ) siano entrambe differenziabili, la regola della catena enuncia che: Nel caso più generale di funzioni multivariate, supponiamo che la funzione differenziabile abbia variabili, e che ogni funzione differenziabile abbia variabili. La regola della catena enuncia che per calcolare la derivata parziale di rispetto ad è sufficiente calcolare: per .
4.6 Algoritmo di backpropagation
L'algoritmo di backpropagation è utilizzato nel calcolo del gradiente della funzione loss rispetto ai parametri (pesi) della rete neurale. In breve, il metodo percorre la rete neurale in verso opposto, dall'output layer all'input layer, e calcola il gradiente sfruttando la regola della catena.
L'algoritmo conserva le derivate parziali intermedie ad ogni iterazione e le ri-utilizza per calcolare altre derivate parziali andando indietro nel grafo computazionale. Ipotizziamo due funzioni e , in cui sono tensori di dimensione arbitraria. Utilizzando la regola della catena, possiamo calcolare la derivata di rispetto ad come segue:
Dove l'operatore prod generalizza la chain rule in base alla dimensione dei tensori. Riprendiamo l'esempio visto nella forward propagation di rete neurale ad un solo hidden layer, in cui è la matrice dei pesi dell'hidden layer, mentre è la matrice dei pesi dell'output layer.
Sia la funzione costo regolarizzata, l'obiettivo della backpropagation è quello di calcolare i gradienti e . Per ottenere ciò, calcoliamo a turno i gradienti rispetto ad ogni variabile intermedia utilizzando la chain rule.
Partendo in ordine inverso, il primo step consiste nel calcolare il gradiente della funzione costo regolarizzata rispetto al termine di loss e rispetto al termine di regolarizzazione . Calcoliamo il gradiente della funzione loss regolarizzata rispetto al risultato dell'output layer , seconda la regola della catena: Calcoliamo il gradiente del termine di regolarizzazione rispetto ad entrambe le matrici di parametri e , ricordando di aver utilizzato la regolarizzazione : È possibile adesso calcolare il gradiente (in questo caso una matrice Jacobiana) della funzione loss regolarizzata rispetto ai parametri dell'output layer utilizzando la regola della catena: Per ottenere il gradiente di rispetto ai parametri dell'hidden layer è necessario continuare la backpropagation dall'output layer all'hidden layer. Il gradiente della funzione loss regolarizzata rispetto all'output dell'hidden layer è dato da: Dato che la funzione di attivazione viene applicata ad ogni elemento di , calcolare il gradiente di rispetto a richiede l'utilizzo dell'operatore di moltiplicazione element wise denotata dal simbolo : In conclusione, è possibile ottenere il gradiente (anche in questo caso una matrice Jacobiana) della funzione rispetto ai parametri dell'hidden layer utilizzando la regola della catena:
4.7 Sommario
Ricapitolando, data una rete neurale ed un training set :
- Si assegna ad una matrice di pesi iniziali scelti casualmente.
- Si addestra la rete neurale con la matrice attuale di pesi su .
- A partire dagli output prodotti dalla rete neurale su e dagli output noti per , viene calcolata la loss media su (su tutti gli esempi del training set).
- Usando l'algoritmo di backpropagation si calcola il gradiente di L rispetto a .
- Si effettua una iterazione del metodo di discesa del gradiente per aggiornare la matrice dei pesi.
- Si iterano i passi da 2 a 5 sino a quando la loss media non decresce più significativamente oppure dopo un numero fissato di iterazioni (dette anche epoche).
4.8 Monitoraggio di qualità
Con i pesi ottenuti ad ogni iterazione del learning sul training set, si testa la rete neurale sul test set e si calcola la loss. L'obiettivo è quello di far diminuire ad ogni epoca il valore della funzione loss sia sul training set che sul test set.
4.8.1 Overfitting
Lo scopo finale del processo di training è minimizzare la loss media su nuovi input. Un problema abbastanza comune è quello di costruire un modello che funziona molto bene sul training set, ma non generalizzabile e funzionante su nuovi input, ovvero il famoso problema dell'overfitting. Le deep neural network sono particolarmente suscettibili all'overfitting, tuttavia esistono dei metodi di regolarizzazione che aiutano a ridurlo.
4.8.2 Aggiunta di penalità
Il metodo di discesa del gradiente potrebbe convergere ad un minimo locale che non corrisponde al minimo assoluto della funzione di loss. Nella pratica si osserva che soluzioni in cui i pesi hanno valori assoluti piccoli producono modelli migliori e più generalizzabili rispetto a soluzioni con pesi grandi. È possibile forzare il metodo del gradiente a favorire soluzioni con peso piccolo aggiungendo un termine di penalità alla loss function usata dal modello: Dove è un iperparametro di tuning che serve a configurare l'importanza della regolarizzazione. Più alti sono i pesi e maggiore è la norma del vettore dei pesi, quindi maggiore è la penalità introdotta. Solitamente si considera la norma 2, ovvero:
4.9 Dropout
Nei capitoli precedenti si è vista la tecnica di bootstrapping utilizzata nella classificazione. Analogamente, viene utilizzata una tecnica che prende il nome di dropout nelle reti neurali. Lo scopo è quello di creare un consenso sui valori ottimali dei pesi, considerando il risultato ottenuto da diverse sottoreti neurali. Ad ogni epoca si seleziona in maniera random una frazione dei nodi della rete, chiamata dropout rate, e si rimuovono. Sulla rete neurale ridotta si effettua una iterazione del metodo di discesa del gradiente. Dal momento in cui la rete neurale completa contiene più nodi rispetto a quella utilizzata durante il training, alla fine del processo di allenamento i pesi ottenuti vengono ri-scalati, ovvero moltiplicati per il dropout rate.
4.10 Early stopping
Nella pratica si osservano comportamenti diversi della funzione di loss sul training set e sul test set. Nel training set la funzione loss decresce durante l'addestramento. Nel test set potrebbe succedere che la funzione loss decresca sino a raggiungere un minimo e, dopo un certo numero di iterazioni, cresca (overfitting). Per evitare questo problema, si può fermare prematuramente il training non appena la loss smette di decrescere nel test set.
Il rischio che si corre con l'early stopping è quello di produrre overfitting sul test set. Per evitare ciò si può costruire un validation set indipendente dai primi due. Si effettua l'early stopping osservando l'andamento dalla funzione loss sul training set e sul validation set. Si ferma il processo quando, mentre la loss sul training set decresce, sul validation set comincia a crescere.
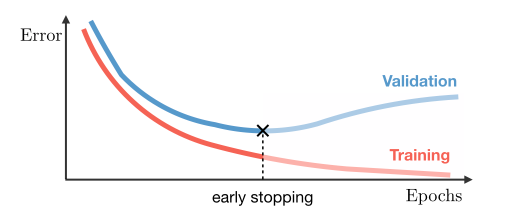
4.11 Aumento del training set
L'accuratezza delle reti neurali è proporzionale alla quantità di dati nel training set. Training set più grandi producono meno overfitting. È possibile arricchire un training set aggiungendo dati artificiali ottenuti applicando trasformazioni ai dati reali o inserendo del rumore. Ad esempio, se la rete neurale è addestrata per classificare immagini (es. convolutional network), si potrebbe incrementare il training set ruotando le immagini o distorcendole con del rumore.
5. Tipologie di reti neurali
5.1 Feed-Forward Networks (FFNs)
Una rete neurale feed-forward ("rete neurale con flusso in avanti") o rete feed-forward è una rete neurale artificiale dove le connessioni tra le unità non formano cicli, differenziandosi dalle reti neurali ricorrenti. Questo tipo di rete neurale fu la prima e più semplice tra quelle messe a punto. In questa rete neurale le informazioni si muovono solo in una direzione, avanti, rispetto a nodi d'ingresso, attraverso nodi nascosti (se esistenti) fino ai nodi d'uscita. Nella rete non ci sono cicli. Le reti feed-forward non hanno memoria di input avvenuti a tempi precedenti, per cui l'output è determinato solamente dall'attuale input.
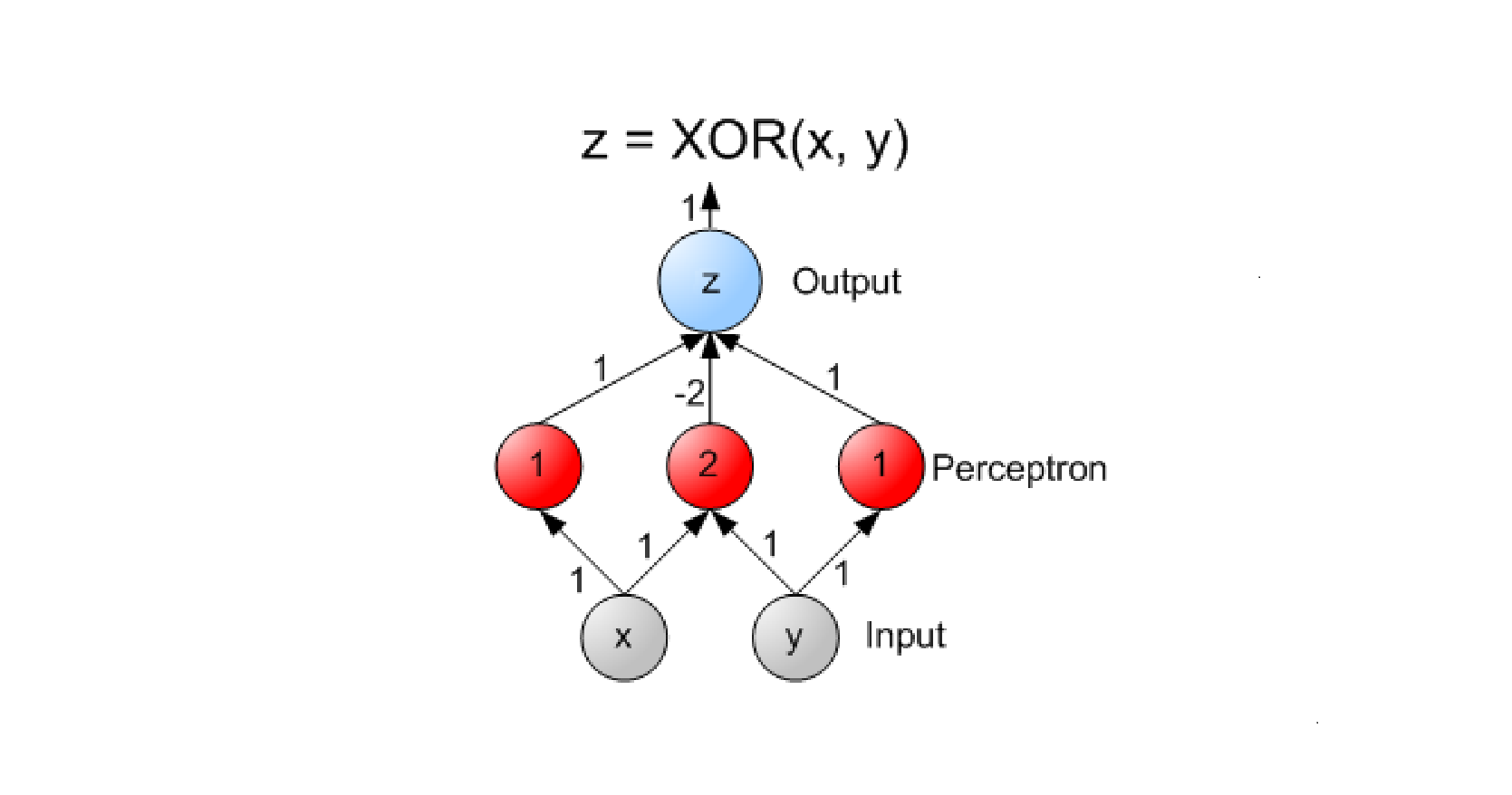
5.2 Convolutional Neural Networks (CNN)
Una rete neurale convoluzionale (CNN o ConvNet dall'inglese convolutional neural network) è un tipo di rete neurale artificiale feed-forward in cui il pattern di connettività tra i neuroni è ispirato dall'organizzazione della corteccia visiva animale, i cui neuroni individuali della retina (fotorecettori) sono disposti in layer. Hanno diverse applicazioni nel riconoscimento di immagini e video, nei sistemi di raccomandazione, nell'elaborazione del linguaggio naturale e, recentemente, in bioinformatica.
Una rete neurale convoluzionale contiene uno o più layer convoluzionali. I nodi all'interno di un layer convoluzionale condividono gli stessi pesi per gli input. Generalmente si alternano i layer convoluzionali a dei layer pooled (o a volte densi) con un numero di nodi progressivamente minore.
Il primo layer coglie le informazioni che rappresentano i pixel essenziali delle immagini, ovvero i contorni. Lo schema di riconoscimento dei contorni è sempre lo stesso e non dipende dal punto in cui viene osservato un contorno (in analogia col fatto che in una CNN i nodi dello stesso layer condividono i pesi degli input). I successivi layer della retina combinano i risultati dei precedenti layer per riconoscere strutture via via più complesse (es. regioni dello stesso colore e infine volti e oggetti).
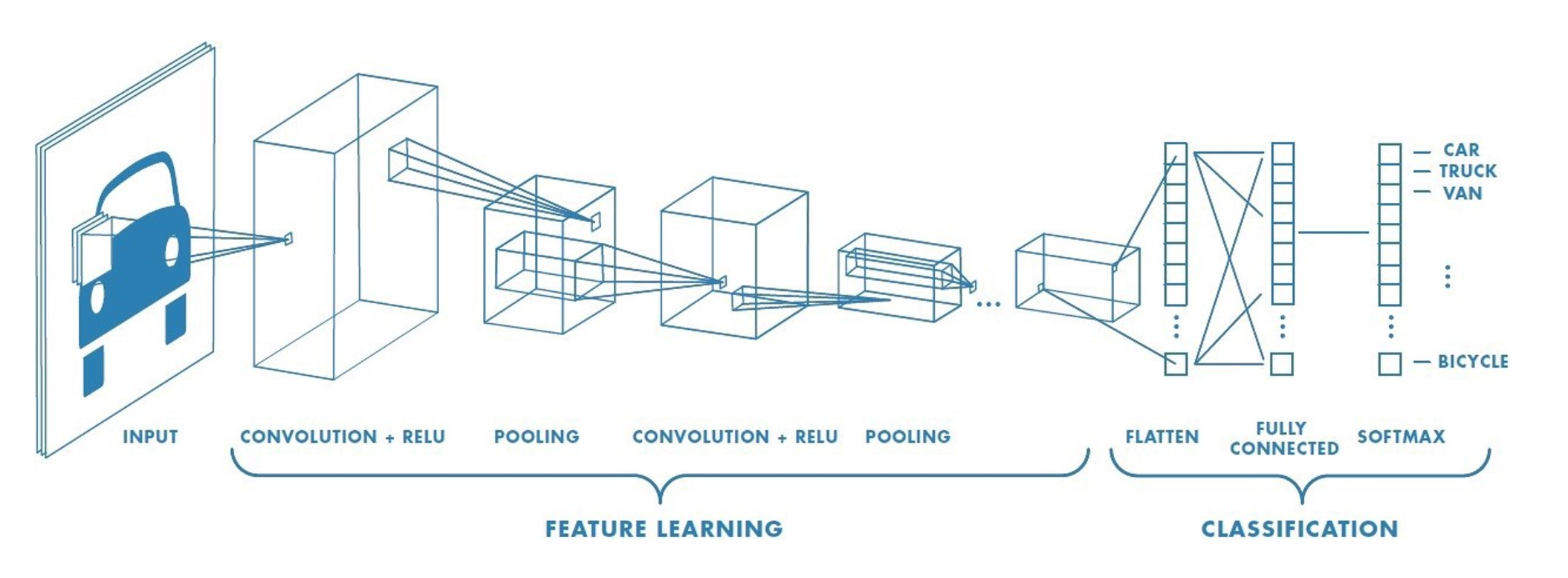
5.2.1 Convolutional layer
Un layer convoluzionale è formato da una griglia di nodi. Ogni nodo può essere immaginato come un filtro di dimensione applicato in un punto della griglia di nodi del layer precedente, ed è detta dimensione del filtro. Nell'ambito dell'image processing, questo equivale ad applicare un filtro in un pixel di una immagine. Se il nodo della convolutional layer applica il filtro sul nodo della griglia di nodi del layer precedente, si considera il quadrato di dimensione il cui vertice in alto a sinistra è e si calcola il valore di output come segue: Se anziché considerare il vertice in alto a sinistra si considerasse il centro, la formula assumerebbe un'altra forma. Per calcolare l'output di tutti i nodi del layer convoluzionale bisogna scorrere il filtro (uguale per tutti i nodi) in lungo ed in largo sulla griglia del layer precedente ed applicarlo. Il risultato è una convoluzione del filtro sull'immagine prodotta dal layer precedente, da cui il nome. Lo stride di un filtro indica di quante posizioni si deve scorrere una volta applicato il filtro. Se allora l'immagine in output avrà la stessa dimensione dell'immagine in input, se allora sarà più piccola.
5.2.2 Zero padding
A seconda delle dimensioni della matrice di input ricevuta, la matrice di output prodotta potrebbe avere dimensioni inferiori anche con stride pari ad 1.Nell'esempio sottostante, partendo dai pixel nell'angolo in basso a destra dell'input potrebbe essere impossibile costruire un quadrato di dimensione . Per ottenere un output delle stesse dimensioni dell'input, una tecnica semplice consiste nell'aggiungere alla matrice di input righe e colonne di . Questa tecnica prende il nome di zero padding.
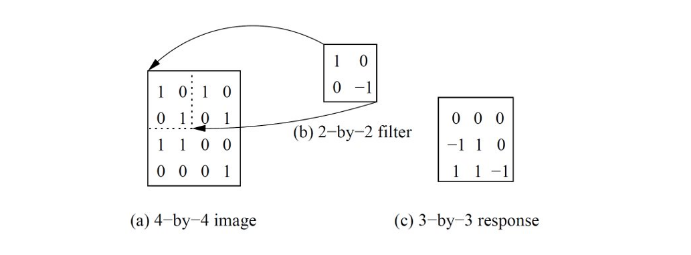
5.2.3 Pooling layer
Un pooling layer prende in input l'output di un layer convoluzionale e produce un output più piccolo. La riduzione è effettuata mediante una funzione di pooling (es. funzione max) che aggrega i valori di una piccola regione intorno all'input. La funzione di pooling agisce su un quadrato di lato di valori di input. Per ottenere l'output completo, il quadrato viene fatto scorrere in lunghezza e larghezza di un valore di stride . Più alti sono i valori ed e più piccolo sarà l'output. Valori troppo grandi di possono portare ad una perdita di informazione.
5.2.4 CNN su immagini a colori
In un'immagine a colori l'input è costituito da 3 canali (RGB). Ogni canale è formato da una matrice di valori (intensità dei pixel). In questo caso, il filtro applicato sia nel convolutional layer che nel pooling layer ha dimensione . Tutti i nodi di uno stesso layer utilizzeranno una matrice di di pesi.
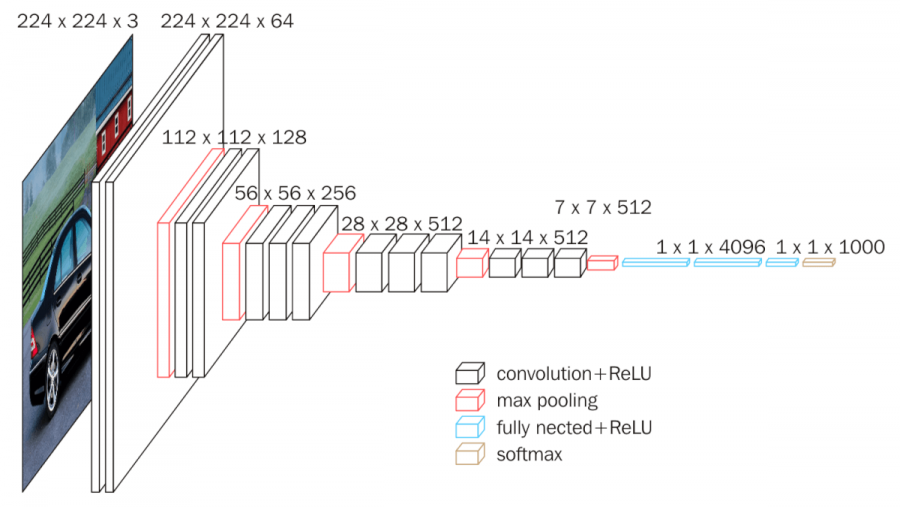
5.3 Recurrent Neural Networks (RNNs)
Una Recurrent Neural Network (RNN) è una rete neurale che può contenere dei cicli. L'output di un layer può diventare l'input per un layer posto precedentemente o per se stesso. Questa disposizione è equivalente ad una rete neurale in cui uno o più layer ricorrono più volte.
I layer ricorrenti possono essere utilizzati come memoria dello stato, per ricordare i valori osservati in passato. Fornendo una sequenza temporale di valori è possibile modellare un comportamento dinamico temporale che dipende dalle informazioni agli istanti di tempo precedenti. Ciò rende le RNN adatte alla predizione di valori successivi a partire da una sequenza di eventi osservati. In breve, mentre le CNN possono processare in maniera efficiente dati tabulari, le RNN sono progettate per gestire al meglio le informazioni sequenziali. Le applicazioni tipiche risiedono nel language processing e nel riconoscimento vocale.
5.3.1 Struttura tipica di una RNN
Definiamo l'input e l'output di un layer ricorrente come due sequenze e . I pesi condivisi dai nodi del layer ricorrente sono rappresentati da 3 matrici come nella figura sottostante. Sia uno stato nascosto che funziona da memoria delle informazioni rappresentate dalla sottosequenza osservata sino al tempo .
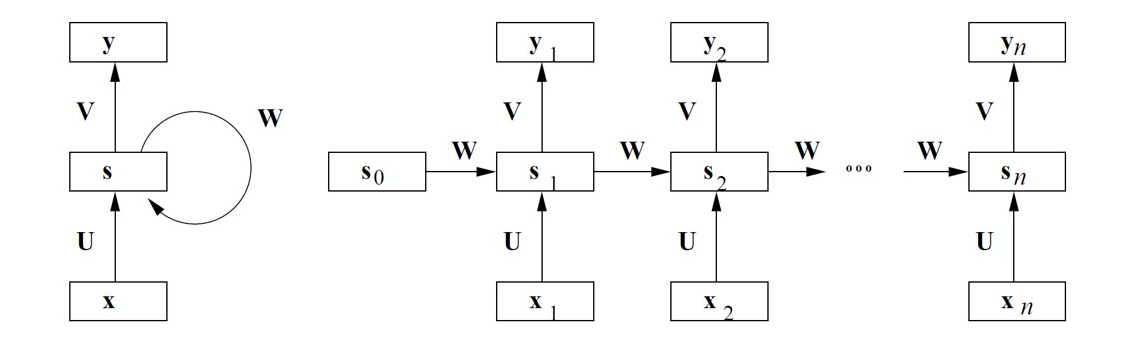
Lo stato nascosto è definito come vettore di zeri. Lo stato nascosto al tempo si ottiene applicando una funzione di attivazione non lineare (es. sigmoid, tanh) considerando l'input al tempo e lo stato nascosto al tempo : Dove è un vettore di bias. L'output al tempo è ottenuto applicando una seconda funzione di attivazione (es. softmax) considerando lo stato nascosto al tempo : Dove è un vettore di bias.
5.3.2 Varianti
In alcune applicazioni (es. la traduzione di una frase) è necessario un unico output da produrre alla fine del processo. In questo caso gli output prodotti ad ogni step dalla RNN vengono passati ad uno o più layer totalmente connessi che genereranno l'output finale.
5.3.3 Sequenze di lunghezza variabile
Per gestire sequenze di lunghezza variabile si possono utilizzare due tecniche:
- Zero padding: si fissa come lunghezza massima della sequenza che la RNN può gestire e, se una sequenza è più corta, si aggiungono zeri fino ad ottenere una sequenza lunga .
- Bucketing: raggruppa le sequenze sulla base della loro lunghezza e costruisce una RNN diversa per ogni valore di lunghezza.
È possibile combinare le due tecniche: si costruiscono diversi bucket, ciascuno dei quali è in grado di gestire sequenze di lunghezza simile in un piccolo intervallo di valori. Si assegna la sequenza in input al bucket in grado di gestire sequenze della stessa lunghezza o di lunghezza leggermente più alta. In quest'ultimo caso si effettua il padding.
5.3.4 Limiti delle RNN
Le RNN sono efficaci solo nell'apprendimento di relazioni o connessioni tra elementi vicini nella sequenza, mentre non sono in grado di apprendere relazioni tra elementi distanti. Ciò può essere problematico nell'apprendimento di un testo. Un verbo o un pronome possono essere separati da molte parole dal soggetto della frase. A livello di calcolo del gradiente, ciò si riflette in una instabilità dei valori, con una saturazione o una esplosione della derivata prima della funzione di attivazione.
5.4 Long Short-Term Memory (LSTM)
La tecnica Long Short-Term Memory (LSTM) è un raffinamento delle RNN che affronta il problema delle connessioni a lunga distanza. Le proprietà di una rete LSTM possono essere riassunte da tre verbi:
- Forget, la capacità di eliminare dalla memoria informazioni che non servono più. Ad esempio, nell'analisi di un testo potremmo scartare informazioni su una frase quando termina.
- Save, la capacità di salvare determinate informazioni in memoria. Ad esempio, nell'analisi di un testo potremmo salvare solo le parole chiave di una frase quando termina.
- Focus, la capacità di focalizzarsi solo su aspetti della memoria immediatamente rilevanti. Ad esempio, nell'analisi di un testo possiamo concentrarci solo su parole che riguardano il contesto della frase attualmente analizzata.
Per realizzare tali proprietà si necessita di una memoria a lungo termine (con informazioni sulla parte di sequenza già analizzata) e di una memoria corrente (con informazioni di immediata rilevanza).

5.4.1 Struttura di una LSTM
Gli stati rapresentano le due tipologie di memoria:
- Stato nascosto: vettore al tempo che indica la memoria corrente;
- Cell state: vettore al tempo che indica la memoria a lungo termine;
IL vettore contiene l'update temporaneo dello stato nascosto. I gate sono vettori usati per far passare selettivamente alcune informazioni di uno stato scartando il resto. Vi sono 3 gate:
- L'input gate determina quali parti del vettore salvare nella memoria long-term;
- Il forget gate che determina quali aspetti della memoria long-term mantenere;
- L'output gate che indica quali parti della memoria long-term spostare nella memoria corrente.
5.4.2 Aggiornamento del cell state
Il primo passo per aggiornare il cell state è calcolare l'update temporaneo dello stato nascosto : Dopodiché si calcolano l'input gate ed il forget gate: Si aggiorna la memoria a lungo termine: Dove sono matrici di pesi e sono vettori di bias. Il simbolo indica il prodotto di Hadamard, ovvero il prodotto puntuale tra vettori o matrici.
5.4.3 Calcolo dello stato nascosto
Per calcolare lo stato nascosco (ovvero la memoria corrente) è necessario calcolare l'output gate E aggiornare la memoria come segue Dove è una matrice di pesi e è un vettore di bias.
5.4.4 Calcolo dell'output
L'output è calcolato allo stesso modo di qualsiasi RNN: Dove è una funzione di attivazione, è una matrice di pesi e è un vettore di bias.
Cenni di analisi testuale
1. Introduzione
L'analisi testuale è la più frequente analisi attuabile nel web e nei social media. Il testo può essere strutturato, ovvero analizzabile in maniera deterministica da calcolatori (es. XML, JSON, codice), o non strutturato, ovvero scritto da esseri umani utilizzano il linguaggio naturale. Nel primo caso abbiamo regole formalizzate per analizzare il testo, ad esempio attraverso le espressioni regolari. Nel secondo caso è necessario adottare tecniche di Natural Language Processing (NLP), che si occupano dell'interazione tra l'umano e il calcolatore attraverso il linguaggio naturale. Le tecniche di NLP sono utilizzate per vari scopi, come l'estrazione di informazioni utili dal testo, categorizzazione del testo, sentiment analysis.
2. Natural language processing
Il Natural language processing è un processo molto sofisticato e può comporsi di vari passaggi. In generale, gli step da portare al termine sono i seguenti:
- Scomporre il testo nei suoi costituenti
- Identificare tali costituenti
- Calcolare statistiche sui tali
- Categorizzare le parole in base alle statistiche
2.1 Word tokenization
Per analizzare un testo bisogna dividerlo prima in una sequenza di token. Un token è una entità comparabile all'interno di un vocabolario di simboli o parole. Dopo aver eseguito la tokenization, è possibile calcolare alcune statistiche basilari, come contare le occorrenze della parola nel testo.
Nel processo di Word Tokenization vi sono alcuni costrutti da comprendere:
- Prefissi: caratteri iniziali (es. $5.00, "" è un prefisso)
- Suffissi: caratteri finali (es. 22km, "km" è un suffisso)
- Infissi: caratteri centrali (es. so-called, "-" è un infisso)
- Eccezioni: particolari regole che permettono di dividere (o non dividere) espressioni in token.
Un esempio di eccezione potrebbe essere la parola "N.Y." che indica "New York". I punti all'interno della parola devono essere considerati in un modo tale da non dividerla in due token differenti. Essendo questo un caso particolare di tokenizzazione, consiste in una eccezione.
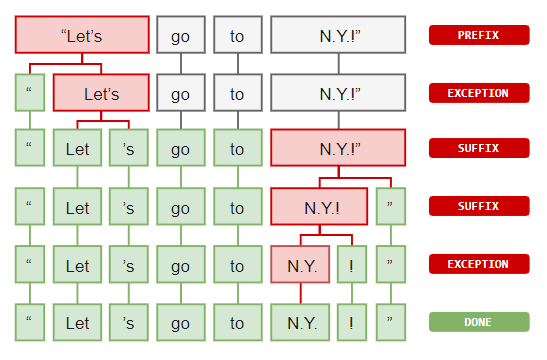
2.2 Stemming
La word tokenization permette di dividere il testo in token, ma più token possono essere diverse coniugazioni dello stesso verbo e quindi indicare lo stesso termine (es. Run, Running \to run). Lo stemming è un processo naive che permette di raggruppare tali varianti in un solo stem (termine originale), rimuovendo la parte finale dalle parole. È necessario notare che l'utilizzo dello stemming riduce la semantica del testo. Un stemmer famoso per la lingua inglese è lo Stemmer di Porter, che consiste in 4 step:

Gli stemmer possono essere inaccurati in alcuni casi, come nelle forme irregolari (ran \rightarrow run). In certi casi, risulta conveniente adottare altri strumenti che vedremo in seguito.
2.3 Lemmatization
A differenza dello Stemming, il processo di Lemmatization consulta vocabolari dei linguaggi per attuare una analisi morfologica alle parole (es. associare was a be), ed analizza il contesto per risolvere ambiguità nell'interpretazione. La raffinatezza dell'algoritmo paga in prestazioni, per cui la scelta dello stemming rimane comunque valida.
2.4 Stop words
Alcuni termini come le congiunzioni, gli articoli, la punteggiatura, non hanno particolare impatto sull'analisi del linguaggio naturale. Tali termini prendono il nome di stop words: il loro contenuto informativo è oggettivamente basso, per cui una parte del processo di NLP prevede spesso la stop words removal, mantenendo solo termini realmente significativi.
2.5 POS - Part of speech tagging
Il linguaggio naturale è ambiguo: la semantica delle parole varia in base al contesto, contiene forme irregolari etc. Un processo nato allo scopo di interpretare ogni singolo termine all'interno di un testo è il Part-Of-Speech tagging (POS tagging). Ad ogni termine viene attribuito un tag, che segue uno standard universale e può essere di due tipi:
- Course-grained tag: un tag grossolano (es. verbo)
- Fine-grained tag: un tag specifico (es. aggettivo possessivo)
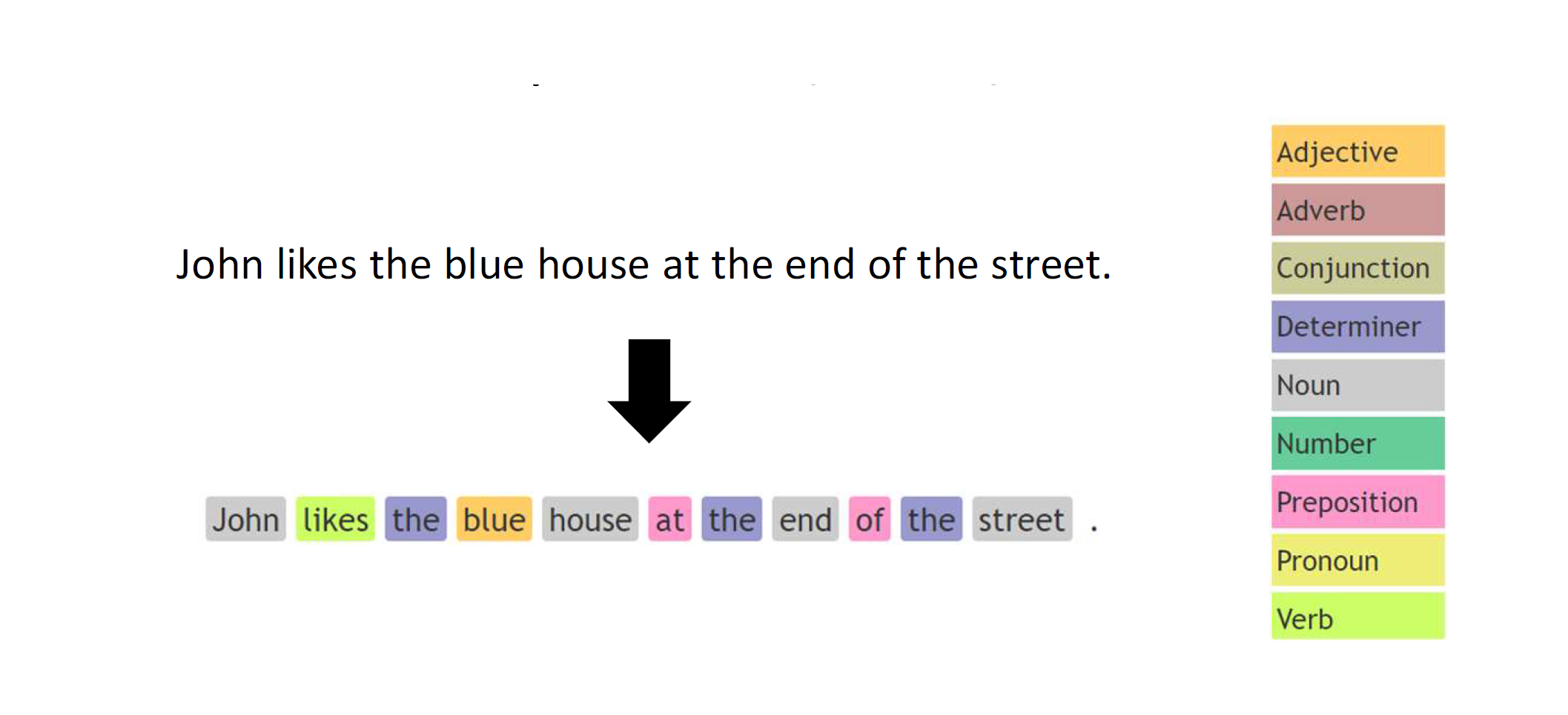
2.6 Named entity recognition
Il processo di Named Entity Recognition (NER) consiste nell’identificazione e nella classificazione di predefiniti tipi di entità all'interno del testo. Esempi classici di entità riconoscibili in un documento sono organizzazioni, persone, luoghi, etc.

2.7 Sentence segmentation
Durante l'analisi di un testo può risultare utile dividere in frasi. Lo scopo potrebbe essere quello di conteggiare le parole per frase, o farne la media. Il processo prende il nome di sentence segmentation e non risulta particolarmente complesso. Gli ostacoli principali di quest'ultimo sono dati dalla punteggiatura: non basta dividere il testo attraverso le occorrenze di ".", ma bisogna talvolta contestualizzare (es. in 25.5% il punto non indica l'inizio di una nuova frase).
2.8 Pipeline generale nella NLP
Riassumendo, il processo di NLP segue spesso la seguente pipeline:
- Word tokenization
- Stop words removal
- Stemming / Lemmatization
- POS tagging (dipende dall'applicazione)
- NER tagging (dipende dall'applicazione)
Chiaramente alcuni step possono essere omessi, altri step potrebbero essere introdotti.
3. Bag of words representation
La bag of words è un tipo di rappresentazione utilizzata nella Information Retrieval e nel NLP per rappresentare documenti testuali ignorando l'ordine delle parole. Permette di considerare la frequenza, o analogamente il conteggio, dei termini all'interno del testo. In tale senso, il documento è visualizzato come una borsa di parole. Le procedure principali per l'estrazione delle parole dal testo sono la word tokenization e molto spesso la stop words removal.
Una volta applicati gli step sul training set composto da documenti da analizzare, i termini risultanti vengono inseriti all'interno di un grande vocabolario V, che avrà una certa cardinalità nd = {t \mid t \in V}DDcd \in Dt \in Vdbow(d) = (c_1, \dots, c_n)nit_id. La rappresentazione attraverso il vettore bow permette all'algoritmo di lavorare con una struttura di lunghezza fissata.
3.1 Normalizzazione ed nbow
Due documenti potrebbero avere frequenze simili, ma una significativa differenza in quantità di parole. Osservando gli istogrammi sottostanti notiamo la similarità tra i documenti D_1D_2t_id Dato che il conteggio dei termini è sempre positivo (al più nullo), la normalizzazione effettuata sarà del tutto equivalente alla normalizzazione L1 (deviazione assoluta). Il risultato delle due normalizzazioni rende molto simili (se non identici) i due grafici.
3.2 TF-IDF
Se consideriamo il caso del rilevamento di posta spam, alcune parole come "Ciao", "Quando", "Buonasera" sono molto frequenti sia nelle mail di spam che nelle mail ordinarie. Parole come "Viagra", "Occasione", "Soldi" sono più comuni nelle email di spam, per cui dovrebbero avere un certo peso nella rilevazione. Tuttavia, con le tecniche adottate sin'ora, se in una mail di 100 parole vi è un'occorrenza della parola "Viagra", essa avrà comunque peso \frac{1}{100}m_it_jd_it_iP(T =t_j)t_j$. Più alta è l'informazione introdotta, più il peso del termine verrà aumentato.
3.3 Bag of things
Anziché basarsi sui termini, un'altro tipo di rappresentazione può considerare stems o vari tags. Elenchiamo alcune rappresentazioni utili: Bag of stems, Bag of POS, Bag of NER, Bag of lemmas. Bag of n-grams.
4. N-gram
Analizzare le singole parole è consono per alcuni task come la spam detection. Tuttavia, la struttura viene completamente andata persa, per cui è possibile che si creino delle ambiguità. Ad esempio:
- Jonh aiuta Robert a cambiare la ruota della macchina;
- Robert aiuta Jonh a cambiare la ruota della macchina;
Le due frasi hanno un significato totalmente diverso, eppure hanno un bag of words identico. Per risolvere tali ambiguità. è possibile raggruppare per 2,3, ..., n parole anziché per una sola parola. Raccogliendo per una parola si parla di uni-gram, per due parole di bi-gram ed in generale per n parole di n-gram. Tanto è grande n, quanto si preserva il contesto e si riducono le ambiguità. Tuttavia, per n grandi il processo di machine learning potrebbe fornire scarsi risultati; inoltre servono più risorse computazionali.
Rappresentazione di immagini
1. Bag of patches
Una immagine non è altro che una matrice di triple di valori. Gli algoritmi di machine learning necessitano di una funzione di rappresentazione per lavorare con le immagini Dove è l'insieme di tutte le immagini. Lavorare considerando una immagine come una sequenza di pixel è molto difficile: un pixel preso singolarmente è poco significativo. Una soluzione consiste nel suddividere l'immagine in patch (porzioni di immagine). Una patch può raffigurare un oggetto o una parte di esso, per cui potrebbe assumere una certa semantica. In questo modo, è possibile considerare una immagine come una sacca di patch (bag of image patches). Una patch in una immagine è equivalente ad una parola in un documento nella rappresentazione bag of words.
1.1 Campionamento delle patch
Per il testo si utilizza la tokenizzazione per estrarre le parole da un documento. Un possibile approccio per ottenere le patch da una immagine consiste nel considerarla come una griglia regolare. Questo approccio semplicistico richiede due parametri: la patch size, ovvero la grandezza delle patch, ed il sampling step, ovvero il numero di pixel di cui dobbiamo spostarci (a destra o in basso) per campionare una nuova patch. In base a tali parametri, è possibile ottenere patch sovrapposte o non sovrapposte. Se allora si avrà sovrapposizione (overlapping) delle patch, altrimenti non saranno sovrapposte.
Una volta campionate ed estratte le patch, ognuna di esse rappresenterà qualcosa (es. un prato, il cielo, una casa, un volto, etc.). Una analisi statistica delle patch può rivelare qualcosa riguardo l'immagine. Ma come assegniamo una certa classe ad una patch? E come creiamo un vocabolario di patch? Il primo passo per rispondere a queste domande è quello di convertire ogni patch in un vettore utilizzando una funzione di rappresentazione adatta.
1.2 Weighted histogram of edge orientation
Partiremo con una rappresentazione basilare per le patch, chiamata weighted histogram of edge orientations. Data un patch in input, il primo step consiste nel convertirla in scala di grigi attraverso una media dei tre canali RGB. Dopodiché si applicano attraverso convoluzione i filtri Sobel X e Sobel Y. Utilizzando i risultati di Sobel X e Sobel Y, che consistono in derivate parziali numeriche, si calcola la magnitudo e l'orientamento dei contorni (edges). Si selezionano gli orientamenti principali e si calcola l'istogramma degli orientamenti degli edge dell'intera patch. Per ridurre il contributo degli edge deboli, esso viene pesato attraverso la magnitudo ed aggiunto nel bin. In un istogramma regolare, ogni qual volta si trova un edge con un orientamento compreso tra e si aggiunge 1 al bin corrispondente. In un istogramma pesato, si considera la magnitudo dell'edge e si somma al bin corrispondente. In qualsiasi caso, l'istogramma può essere normalizzato dividendo ogni bin per la somma di tutti i bin.
Essendoci 8 orientamenti principali (quindi 8 bin), questa rappresentazione mappa ogni patch dell'immagine in un vettore di dimensione 8. Patch simili avranno istogrammi simili, viceversa per patch differenti.
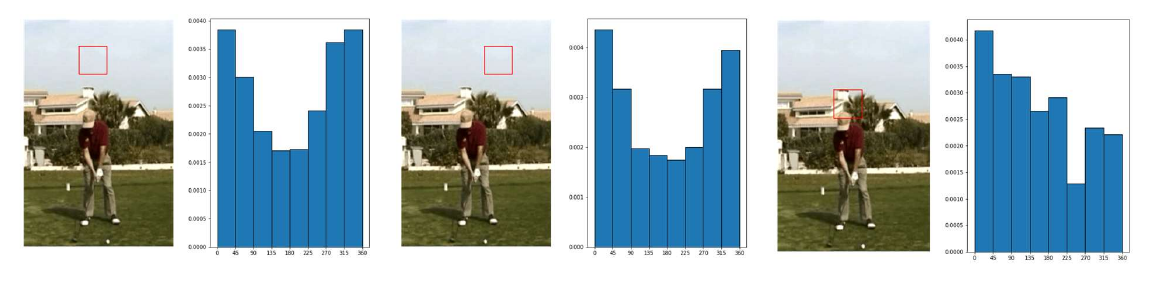
1.3 Sift descriptor
Il metodo precedente è limitato quando si presentano strutture complesse. Un metodo più elaborato, basato anch'esso sul weighted histogram of edge orientation, è il SIFT descriptor. La parola descriptor indica che l'algoritmo è utilizzato per descrivere le patch di una immagine. L'idea principale è semplice:
- Si divide la patch in una griglia
- Per ogni cella della griglia si calcola l'istogramma pesato
- Tutti gli istogrammi sono concatenati in un vettore da elementi
Il descrittore SIFT permette di mappare una patch in un vettore di dimensione 128, molto più espressivo rispetto ad un singolo istogramma.
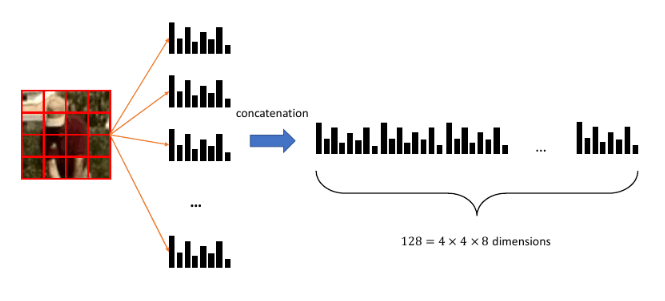
1.4 Definizione di un vocabolario
Allo scopo di fornire una rappresentazione di dimensione fissa, è necessario definire un vocabolario. Consideriamo un insieme di immagini e, per ognuna di esse, estraiamo le patch e calcoliamo i SIFT descriptor. Se assumiamo che patch simili hanno SIFT descriptor simili, allora possiamo utilizzare le tecniche di clustering per identificare un numero limitato di patch per comporre il vocabolario. Chiameremo visual words i centroidi di ogni cluster. Quando arriva una nuova patch, si utilizza il modello di clustering per assegnarla ad un cluster.
1.5 Bag of visual words
I paragrafi precedenti descrivono gli elementi principali della rappresentazione bag of visual words (analoga alla r. bag of words). Consideriamo un training set di immagini, la procedura completa è la seguente:
- Si estraggono le patch da ogni immagine in
- Ogni patch sarà descritta con un vettore di dimensione 128 calcolando il SIFT descriptor
- Si applica un algoritmo di clustering sulle patch e si ottengono cluster
- Ogni cluster ha un centroide, denominato visual word, che viene inserito nel vocabolario
- Anche la visual word è rappresentata con un descrittore SIFT
- Il numero di parole nel vocabolario equivale al numero di cluster
Una volta costruito il vocabolario, è possibile ottenere la rappresentazione bag of visual words di una immagine come segue:
- Si estraggono le patch dall'immagine
- Per ogni patch si calcola il descrittore SIFT
- Si assegna ogni descrittore ad una visual word del vocabolario attraverso un classificatore kNN
Ad ogni immagine sono assegnati un certo numero di visual words appartenenti al vocabolario, per cui si può proseguire con tutte le tecniche viste nella rappresentazione bag of word (es. normalizzazione, TF-IDF). Questa tecnica funziona anche per immagini di diversa risoluzione.
1.6 Content-Based Image Retrieval
La Content-Based Image Retrieval (CBIR) è una interessante applicazione delle tecniche di rappresentazione delle immagini. Consiste nel cercare immagini simili ad una immagine query in un grande dataset di immagini. Disponendo di una buona funzione di rappresentazione, il task è banalmente risolvibile con una ricerca nearest neighbor.
Per esempio, data una immagine query, si può calcolare la distanza delle rappresentazioni tra la query e le altre immagini nel dataset. Dopodiché si può ordinare il dataset in base alla distanza e prendere i primi risultati. Questo approccio è del tutto equivalente al kNN.
Sentiment Analysis
1. Semantics in Text Analysis
Sinora le parole all'interno di un documento hanno avuto una funzione prettamente statistica, considerate come un mero simbolo privo di significato. Questi approcci non tengono conto della semantica delle parole e delle relazioni tra esse, ad esempio:
- All you need is love
- I believe that the heart does go on
La semantica delle due frasi suggerisce che esse sono simili, ma utilizzando una rappresentazione puramente statistica, come la bag of words, le frasi saranno quanto più distanti possibile. Per associare le due frasi abbiamo bisogno di una funzione distanza che misuri il grado di similarità semantica tra parole.
1.1 Contesto di una parola
Per misurare la distanza tra parole dobbiamo prima mapparle in uno spazio comune attraverso una funzione di rappresentazione . Dopodiché possiamo misurare la loro distanza attraverso una funzione distanza (es. distanza Euclidea). La proprietà desiderata è che parole con una semantica simile devono trovarsi vicine.
Consideriamo una parola in un documento, chiameremo contesto della parola quell'insieme di parole che appare in una finestra di una data dimensione centrata nella parola.
The quick brown fox jumps over the lazy dog
Ipotizziamo che la parola sia fox e che la dimensione della finestra sia , allora il contesto di fox sarà: Parole simili sono utilizzate in modi simili in frasi differenti, per cui parole simili avranno contesti simili. Chiameremo questo tipo di rappresentazione word embeddings.
1.2 Matrice di co-occorrenza
Dato un corpus di documenti ed un vocabolario , la matrice di co-occorrenza sarà tale che l'elemento conterà il numero di volte che la parola occorrà nel contesto della parola . Definiremo
Dato un corpus di documenti ed un vocabolario , la matrice di co-occorrenza è tale che:
- L'elemento indica il numero di volte in cui la parola occorre nel contesto della parola .
- L'elemento indica il numero di volte in cui ogni parola apparen nel contesto della parola .
- Definiamo la probabilità che appaia nel contesto di .
1.3 GloVe
GloVe, coniato da Global Vectors, è un modello per la rappresentazione distribuita di parole. Affronteremo tale algoritmo in maniera generale, esplorando l'idea principale senza scendere nel dettaglio.
Sia una parola, vogliamo ricavarne l'embedding, ovvero una rappresentazione di dimensione fissa . La coppia di parole è caratterizzata dalla probabilità . Abbiamo assunto che parole simili hanno contesti simili, per cui due parole simili saranno tali che: Imponendo che: Allora gli embeddings soddisferanno la proprietà desiderata: Nella pratica risulta più semplice imporre Poiché Dato che il termine non dipende dalla coppia di parole possiamo scartarlo ed imporre: Il che garantirà comunque che parole simili avranno embedding simili. Per apprendere degli embedding funzionanti, definiamo una funzione costo da minimizzare: Dove rappresenta la matrice la cui -esima riga corrisponde all'embedding della -esima parola. Minimizzare tale funzione vuol dire trovare degli embeddings in cui risulti pseudo-valida l'espressione . Il logaritmo non può essere calcolato nel caso in cui , per cui si introduce una funzione definita come segue: Dove generalmente e . Ridefiniamo la funzione costo Quando l'espressione all'interno della sommatoria sarà nulla, altrimenti varrà al più 1. Per minimizzare la funzione si utilizza l'algoritmo di discesa del gradiente o il metodo dei minimi quadrati:
1.4 Geometria delle parole
Si è scoperto che le relazioni semantiche tra parole vengono riflesse geometricamente nello spazio di rappresentazione. Ad esempio, la distinzione tra le parole "re" e "regina" o "fratello" e "sorella" è della stessa natura della distinzione più generale tra "uomo" e "donna". Matematicamente, ci aspettiamo che i vettori differenza tra le parole sopracitate (rappresentate come word embedding) siano pressoché uguali.
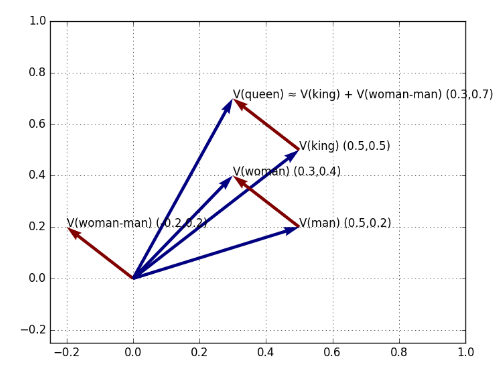
Tale proprietà consente di applicare la matematica dei vettori di parole. Se il vettore differenza è uguale al vettore differenza allora, conoscendo solo il vettore e partendo dal vettore è possibile calcolare il vettore della parola "queen" come segue:
2. Sentiment analysis
Il sentiment analysis (o opinion mining) è lo studio computazionale dell'opinione, del sentimento e delle emozioni delle persone rispetto a prodotti, servizi, organizzazioni, individui, eventi o topic e i loro attributi (Liu, 2015). Dato un testo contenente delle opinioni, lo scopo di un algoritmo di sentiment analysis è quello di capire se l'emozione dell'autore è positiva o negativa, o in generale studiarne il sentimento.
2.1 Primi approcci
Un primo approccio al sentiment analysis interpreta il problema come un task di classificazione, in cui il testo può essere positivo o negativo. In tal caso, vi sarà un dataset contenente esempi positivi e negativi. Si potrebbe utilizzare la rappresentazione bag of word per allenare un regressore logistico a tale scopo.
2.2 Vader
Se alleniamo il regressore logistico su valutazioni cinematografiche, non è detto che lo stesso modello sia adatto ad analizzare testi provenienti da altri domini (es. i social media). L'algoritmo Vader superà tale difficoltà effettuando una analisi basata sui lessici di parole legate al sentimento (lexicon of sentiment-related words). Un lexicon può essere una parola, uno slang o un emoticon. Ogni lexicon è stato valutato da esseri umani con un numero da (negativo) a 4 (positivo). Dopo aver raccolto tutte le valutazioni, è stato assegnato ad ogni lexicon uno score ottenuto attraverso una media.
Lo scopo di Vader è quello di calcolare il punteggio del sentimento di una intera frase. Questo è fatto sommando il sentiment score di ogni lexicon contenuto nella frase:
Dove è l'-esima parola ed è la funzione che ne restituisce il sentiment score. Lo score è normalizzato utilizzando la seguente formula:
Dove . Il grafico sottostante visualizza gli effetti della normalizzazione. All'aumentare del valore assoluto di il sentimento totale converge a -1 o ad 1.
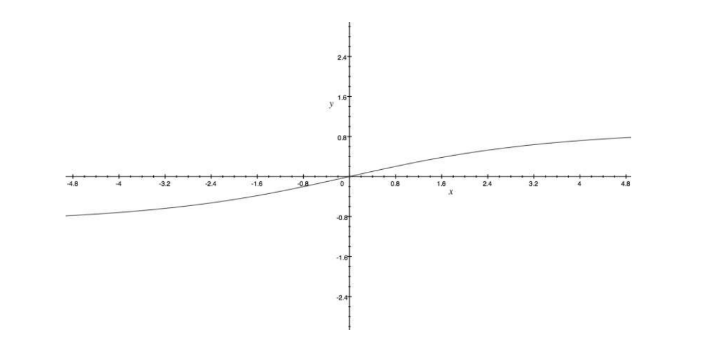
2.2.1 Punteggiatura
Dopo aver calcolato il sentiment score dell'intera frase, l'algoritmo Vader controlla la punteggiatura. Questo controllo è motivato dall'euristica secondo il cui la punteggiatura aumenta l'espressività della frase e quindi il sentimento ad essa associato. Le regole sono le seguenti ed i valori sono risultati empirici: se il sentimento è positivo, Vader aggiunge per ogni punto esclamativo e per ogni punto interrogativo, se il sentimento è negativo li sottrae.
2.2.2 Capitalizzazione
Similmente, scrivere in maiuscolo enfatizza il concetto nella frase, per cui per ogni parola capitalizzata Vader aggiunge se il sentimento è positivo, li sottra se è negativo.
2.2.3 Modificatori di grado
Modificatori del tipo "very" o "sort of" posso essere utilizzati per amplificare o diminuire il sentimento di una determinata parola. Vader contiene un dizionario di boosters e dampeners (stabilizzatori). Un modificatore posto di fianco ad una parola sottrae (se la parola è negativa) o aggiunge (se è positiva) al sentiment score totale. Un secondo modificatore aggiunge o sottrae il % di , un terzo aggiunge o sottrae il % e così via.
2.2.4 But
Spesso un "ma" può cambiare la polarità della frase, ad esempio "ti amo, ma non voglio più stare con te" è una frase negativa anche se "ti amo" ha uno score prettamente positivo. Vader contiene un "but" checker che decrementa del 50% lo score della frase antecedente al "but" ed incrementa del 50% lo score della parte seguente.
2.2.5 Negazioni
Un insieme di espressioni può essere utilizzato per capovolgere il sentimento associato ad una parola, ad esempio "isn't really that great" cambia la polarità della parola "great". Vader controlla questi casi analizzando i trigrammi precedenti ad ogni parola. Quando il trigramma rientra nella lista delle possibili negazioni, il sentimento della parola è decrementato di .
2.2.6 Output di Vader
Per ogni testo analizzato, Vader ritorna una lista di valori:
- Positive: la percentuale di parole positive
- Neutral: la percentuale di parole a cui non è associato un sentimento
- Negative: la percentuale di parole negative
- Compound: il sentiment score della frase
Hadoop
Hadoop è un framework opensource (progetto Apache, sviluppato da Yahoo). Lo scopo di Hadoop è quello di immagazzinare e processare dataset in scala massiva. Hadoop può girare su un cluster di comodity hardware. Le seguenti componenti formano il core del framework:
- HDFS, un file system distribuito
- MapReduce, modello di programmazione per large scale data processing.
Hadoop astrae la complessità dietro i sistemi distribuiti, permettendo a programmatori senza alcuna competenza nel campo di poter utilizzare facilmente le risorse di un data center per elaborare grandi moli di dati.
Large scale computing
Per processare grandi moli di dati vi sono due tecniche:
- Scale up: aumentare le prestazioni di un singolo nodo
- Scale out: aumentare il numero di nodi
Nella maggior parte dei casi conviene adottare la seconda tecnica: si utilizza un cluster formato da commodity hardware, ovvero hardware economico, facilmente reperibile, e si organizza il computing dei dati in modo parallelo. Con lo scale out è necessario organizzare il processing dei dati in maniera distribuita, quindi orchestrare i nodi, adottare tecniche di fault tolerance nel caso di guasti, trasportare i dati da un nodo ad un altro etc.
Hadoop risolve elegantemente questi problemi:
- Provvede un file system distribuito, astraendo le complicazioni sottostanti e permettendo al programmatore di accedere ai dati come in un normale file system.
- Introduce un modello di programmazione orientata al calcolo distribuito, ovvero Map-Reduce.
Concetti chiave
L'infrastruttura dello storage HDFS è formata da:
- Datanode, nodi che contengono e trasferiscono dati
- Namenode, localizza i file nei datanode (orchestratore)
I file sono divisi in blocchi e replicati sui datanode (replicazione spesso su diversi rack). Chunk da 16-64 mb vengono inviati ai workers per la computazione. L'utente può scegliere il grado di replicazione e la dimensione dei chunk.
L'infrastruttura della componente MapReduce è la seguente:
- Masternode, che orchestra la computazione
- Workers, effettuano la computazione
Ogni programma che gira su Hadoop rispetta la seguente pipeline (modello MapReduce):
- iterare su un grande numero di record in parallelo
- Ad ogni iterazione, estrarre delle informazioni
- Eseguire uno shuffling ed un sorting dei risultati intermedi
- Aggregare i risultati intermedi
- Generare il risultato finale
Vi sono due sole primitive:
- La map prende in input un oggetto con una chiave ed un valore e restituisce un elenco di coppie chiave valore . Il framework (Hadoop) colleziona tutte le coppie con la stessa chiave e associa a tutti i valori .
- La reduce prende in input una chiave ed una lista di valori e li combina in qualche modo.
Ai nodi workers possono essere affidati task di map e di reduce. Solitamente lo scheduler assegna i task di map ai nodi che hanno i dati vicini, per risparmiare sul tempo. I risultati intermedi delle operazioni di map sono conservati nel file system locale dei nodi workers che li hanno svolti.
Quando un nodo worker ha finito un task di map, produce file intermedi (uno per ogni reduce instanziata) e avverte il master. Il master comunica la posizione dei file ai reducer instanziati.
Se un worker è lento allora tutta la computazione sarà lenta. Per questo il masternode può assegnare lo stesso task a più worker. Chi finisce prima "vince" e segnala i risultati al masternode, mentre gli altri worker verranno interrotti.
Quando la funzione reduce è commutativa e associativa è possibile anticipare la computazione con dei combiners: si aggregano i dati intermedi direttamente nel nodo worker che li ha prodotti.
Se si vuole controllare come le chiavi vengono partizionate negli file intermedi, si può utilizzare un partitioner, definendo una hash function propria.
Al resto ci pensa il framework Hadoop: quando lo sviluppatore sottomette il job, hadoop penserà a:
- Gestire lo scheduling
- Gestire la distribuzione dei dati
- Gestire la sincronizzazione dei risultati
- Gestire fallimenti ed errori
- Gestire il file system distribuito
Molto spesso il numero di task istanziati eccede il numero massimo di task eseguibili in maniera concorrente, per questo lo scheduler tiene una coda dei task, eseguiti ogni qual volta un worker è disponibile.
Proprietà di Hadoop
- Data locality: dati e worker devono essere vicini
- Architettura senza condivisione: ogni nodo è indipendente e autosufficiente
- Localizzazione: porta il worker dai dati e non viceversa (così da non far spostare i dati nella rete)
- Sincronizzazione: tra le map e le reduce, tramite raggruppamento per chiavi (ottenuto tramite sorting dei risultati intermedi).
- Gestione fallimenti:
- map failure: si rischedula il task su un altro worker e si notificano i reducer.
- reducer failure: si rischedula il task su un altro worker.
- master failure: aborto del job e notifica al client.
Natural join example
Abbiamo due tabelle e . Vogliamo calcolare la natural join tra queste ultime.
def R_map(k, v):
b = v[1]
a = v[0]
emit(b, (a, "R"))
def S_map(k, v):
b = v[0]
c = v[1]
emit(b, (c, "S"))
def natural_join_reduce(k, w):
b = k
a_set = [ v[0] if v[1] == "R" for v in w ]
c_set = [ v[0] if v[1] == "S" for v in w ]
for a in a_set:
for c in c_set:
emit(a, b, c)
Yarn
YARN (Yet Another Resource Negoziator) è la componente di Hadoop che si occupa di generare e coordinare i map/reduce task (master). È composto da tre pezzi:
- Resource manager
- Node manager
- Application master
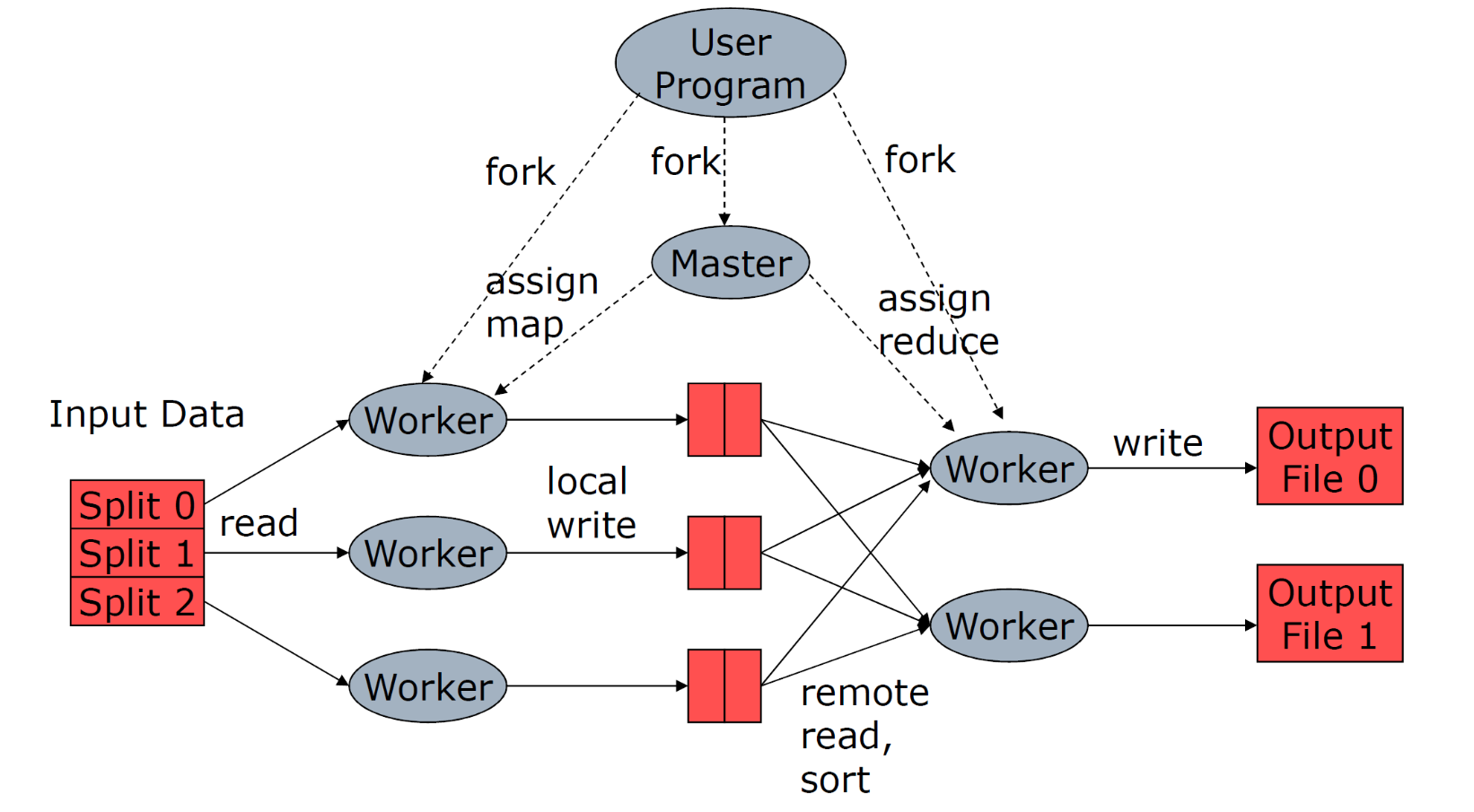
Assegnazione dei task
Hadoop permette di specificare il grado di parallelismo di ogni macchina in configurazione, esprimendo il numero di slot. Un slot è un contenitore in cui può finire un map/reduce task in esecuzione.
Matrix-Vector multiplicatione example
Sia una matrice di dimensione . Sia un vettore di dimensione . La moltiplicazione matrice-vettore produce un vettore di lunghezza dove: Supponiamo che e siano file su HDFS. Ogni entry della matrice può essere conservata esplicitamente come (stessa cosa per ).
Se riesce ad entrare in memoria centrale, possiamo scrivere la seguente procedura:
def map(k,v):
v = get_v_from_cache()
i = v[0]
j = v[1]
m_ij = v[2]
v_i = v[i]
emit(i, (v_i * m_ij))
# w conterrà i risultati di tutti
# i prodotti di indice "i"
def reduce(k, w):
i = k
x_i = 0
for v in w:
x_i += v
emit(i, x_i)
Se non entra in memoria, allora si dividono sia la matrice che il vettore in fasce:
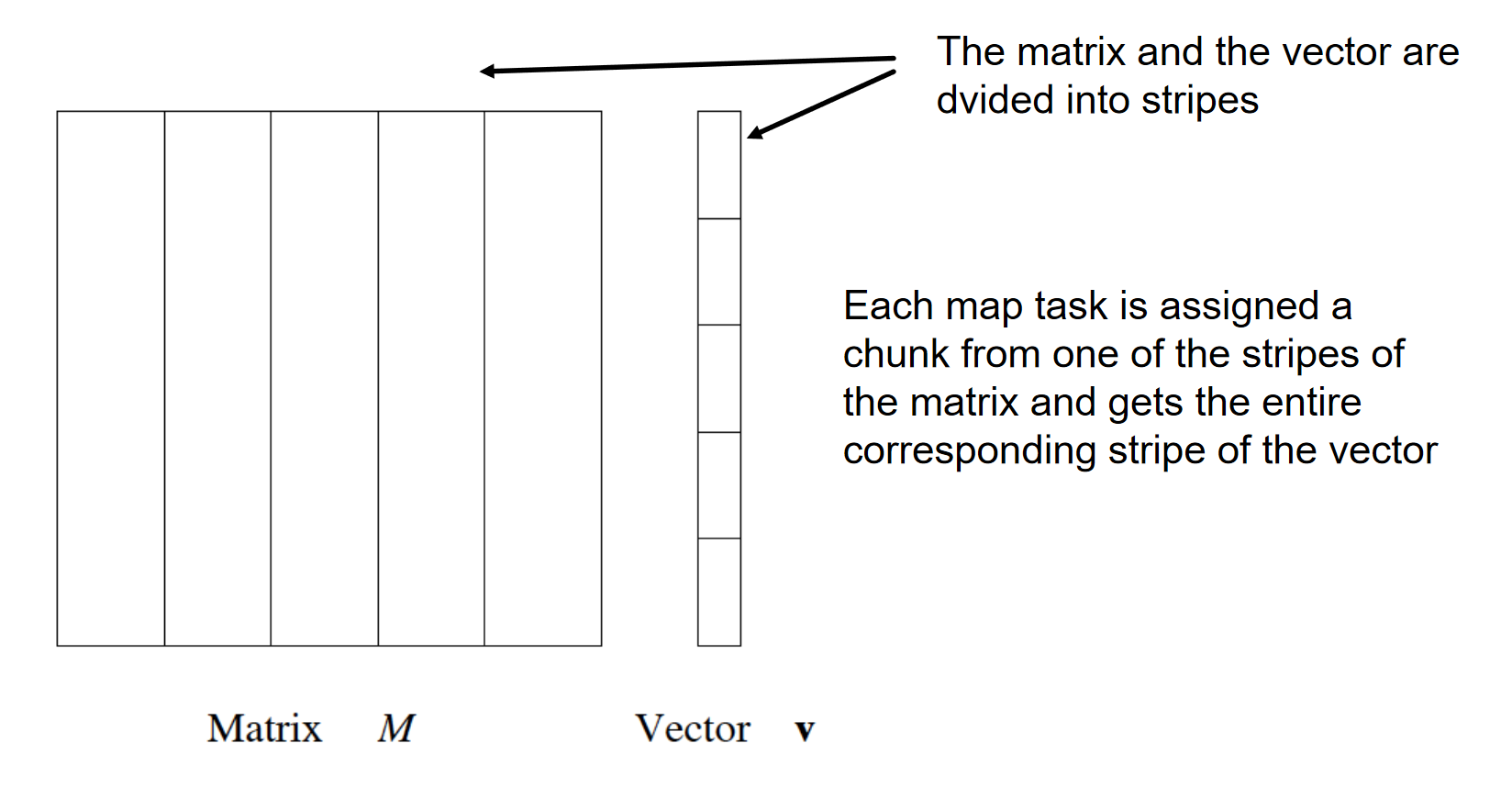
Quando si assegnano ai worker i map-task si passano dati i dati di uno stripe della matrice e del corrispondente stripe del vettore.
Matrix multiplication example
Siano e due matrici entrambi di dimensione .
# il valore è (i, j, m_ij). Invia come chiave
# la colonna j e come valore "M" (identificativo),
# i (la riga) ed m (il valore).
def M_matrix_map(k, v):
i = v[0]
j = v[1]
m = v[2]
emit(j, ("M", i, m))
# il valore è (j, k, n_jk). Invia come chiave
# la riga j e come valore "N" (identificativo),
# i (la riga) ed n (il valore).
def N_matrix_map(k, v):
j = v[0]
k = v[1]
n = v[2]
emit(j, ("N", k, n))
# si dividono gli elementi raggruppati sono la chiave
# "i" e si dividono in base alla matrice di provenienza.
# Si itera tra gli elementi di M e poi tra gli elementi di
# N e si performa il prodotto la riga di M e la colonna di
# N. Si emette come chiave (i, k) (riga di M e colonna di N)
def prod_reduce(k, w):
j = k
j_cols_M = [ m if v[0] == "M" for v in w ]
j_rows_N = [ n if v[0] == "N" for v in w ]
for (_, i, m_ij) in j_cols_M:
for (_, k, n_jk) in j_rows_N:
emit((i,k), (m_ij * n_jk))
# funzione identità
def identity_map(k, v):
emit(k, v)
# Si raggruppano i prodotti che formano l'elemento
# (i,k) nella matrice risultante e si sommano.
# si emette (i,k) come chiave ed il valore dell'elemento
# come valore.
def sum_reduce(k, w):
return (k, sum(w))
2. Advanced Market Basket Analysis
Definizioni preliminari: il power set di un insieme è l'insieme de
2.1 PCY Algorithm
L'algoritmo PCY (Park-Chen-Yu) applica una modifica all'algoritmo classico Apriori. Nel primo step dell'apriori, quando si effettua il conteggio degli item nei basket, la maggior parte della memoria principale resta inutilizzata. Questo algoritmo sfrutta la memoria in idle per risparmiare alcuni calcoli nello step successivo.
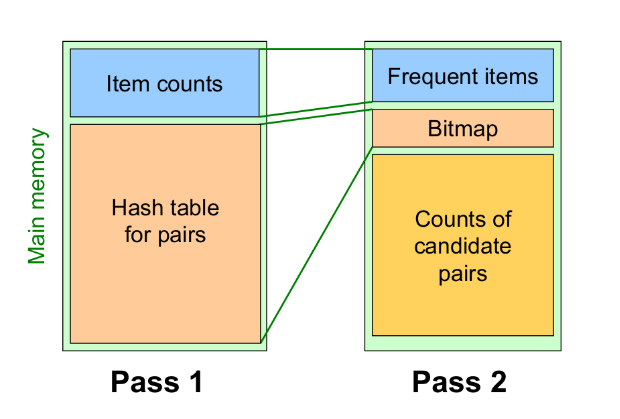
2.1.1 L'algoritmo
Sia una funzione hash e supponiamo che la memoria in idle sia sufficiente a far entrare bucket. La funzione hash potrebbe, ad esempio, essere definita come segue La funzione prende in input coppie di item e da in output uno tra i bucket. Quando si scansionano i carrelli per il conteggio degli item, per ogni coppia contenuta nel carrello si calcola l'hash della coppia , si inserisce la coppia nel bucket -esimo e si incrementa il conteggio delle coppie per quest'ultimo.
Notiamo che, se , allora sicuramente le coppie di item che finiranno in bucket con un conteggio minore di 2 non saranno frequenti. Tuttavia, la tabella hash è pesante da mantenere in memoria, quindi scremiamo la struttura creando un array di bit di lunghezza (uno per ogni bucket), in cui asseriamo solo i bit il cui corrispondente bucket ha un conteggio maggiore o uguale a . Eliminiamo dalla memoria la tabella hash e manteniamo l'array di bit. Nella generazione delle coppie candidate ad essere frequenti, controlliamo con la funzione di hash se ricade in un bit posto a 0, ed in tal caso scartiamo la coppia, o posto ad 1, quindi la manteniamo come candidata.
Supponendo che, al posto della tabella hash, si fosse tenuto in memoria il vettore dei conteggi, ogni conteggio avrebbe occupato 4byte. Con il vettore di bit, per ogni bucket si occupa di quello che si occuperebbe utilizzando il conteggio.
Questo metodo non ammette falsi negativi: se il conteggio di un bucket non supera la soglia , allora una coppia contenuta nel bucket, che sarà presente nei carrelli al più tante volte quanto è il conteggio nel bucket, non supererà anch'essa la soglia.
Osservazione: se al conteggio delle coppie utilizziamo una matrice triangolare, lo spreco in termini di spazio è lo stesso (se non maggiore, a causa del vettore di bit) dell'apriori tradizionale. Se con la tabella hash riuscissimo ad eliminare almeno dei candidati, allora potremmo utilizzare una tabella di triple (item, item, count) e risparmiare comunque spazio, avendo un algoritmo più performante sotto tutti gli aspetti.
2.1.2 Raffinamento
Un ulteriore raffinamento consiste nell'utilizzare più funzioni hash, vediamo due metodi: il multistage ed il multihash.
Nel metodo multistage si aggiunge un passo intermedio dove, ai risultati dell'hashing al passo uno, viene applicata una ulteriore funzione hash e prodotto un ulteriore bit-vector con meno falsi positivi. Questo metodo richiede tre passaggi.
Nel metodo multihash si utilizzano già al passo uno due funzioni hash ed . Si tengono due tabelle hash in memoria che mantengono il conteggio degli elementi. Alla fine si producono 2 bit vector e . Una coppia sarà selezionata come candidata se e solo se i bit, per entrambe funzioni hash, in AND risultano 1, altrimenti in uno dei due conteggi la coppia non risulta frequente.
2.2 Random sampling
L'algoritmo random sampling proviene dalla statistica: possiamo pensare che prendendo un campione del nostro insieme di carrelli, e riducendo anche la soglia di frequenza (ad esempio ), i risultati siano pressoché quelli reali, ammettendo un certo numero di falsi positivi e falsi negativi.
Osservazione: ridurre eccessivamente la soglia comporta che la maggior parte degli insiemi saranno considerati frequenti, quindi un'aumento dell'utilizzo della memoria.
Nello specifico, prendiamo un campione dalla popolazione che entri in memoria principale. Così facendo, risparmiamo nei tempi di IO dell'algoritmo ed operiamo in-place. Opzionalmente, è possibile verificare che le coppie risultate frequenti siano realmente frequenti sul dataset originale.
2.3 SON Algorithm
L'algoritmo SON (Savasere-Omiecinski-Navathe) consiste nel leggere dal disco sottoinsiemi di basket di grandezza proporzionale alla memoria, e dopodiché eseguire l'apriori (in memoria) su di essi, scalando opportunamente la soglia . Un itemset diventa candidato ad essere frequente se è frequente in almeno uno dei sottoinsiemi processati. In un secondo passaggio, si verifica che i candidati ad essere frequenti siano frequenti in tutto il dataset. Anche in questo algoritmo si sfrutta l'idea chiave della monotonicità: un insieme non può essere frequente se non lo è almeno in un sottoinsieme.
2.3.1 Algoritmo distribuito
La computazione del SON è particolarmente semplice da distribuire su più calcolatori: ogni calcolatore prende un sottoinsieme del dataset di carrelli e processa il risultato. I risultati vengono distribuiti e viene accumulato il loro conteggio. I candidati vengono poi verificati in un secondo passaggio.
2.3.2 Map-Reduce
Implementiamo le due fasi dell'algoritmo secondo il paradigma map-reduce, sfruttando 2 map-reduce in cascata.
Fase 1 - trovare i candidati
Ad ogni nodo viene inviato un sottoinsieme del dataset di carrelli. Ogni chunk conterrà come valore un elenco parziale di transazioni (carrelli), mentre la chiave non sarà importante. Scaliamo il supporto in base al numero di chunk prodotti, quindi riferiamoci al supporto scalato (o locale) come .
# k (chiave): nulla
# v (valore): elenco parziale di basket
# sl: supporto locale
# apriori: algoritmo apriori che prende in input set di basket ed un supporto.
# emit: emette una coppia (chiave, valore)
def map(k,v):
IS = apriori(v, Sl)
for itemset in IS:
emit(itemset, 1)
# k (chiave): itemset frequenti in (almeno) un sottoinsieme
# v (valore): 1 (non serve)
def reduce(k, v):
emit(k, 1)
Fase 2 - trovare gli insiemi frequenti
Mettiamo in cache i candidati ottenuti dalla fase 1 in un insieme . Nuovamente inviamo ad ogni nodo un sottoinsieme del dataset di carrelli. Nella map, per ogni itemset candidato si conteggia il supporto locale nel sottoinsieme di carrelli e si emette. Nella reduce, si sommano i supporti locali per ogni itemset e, se il supporto totale supera la soglia , allora si emette l'itemset frequente ed il suo supporto.
# C : candidati in cache ottenuti dalla fase 1
# k (chiave): nulla
# v (valore): elenco parziale di basket
# count: conteggia le occorrenze dell'itemset nell'elenco parziale di basket
def map(k,v):
for itemset in C:
supp = count(itemset, v)
if (supp > 0):
emit(itemset, supp)
# k (chiave): itemset
# v (valore): insieme dei supporti per ogni subset di carrelli
# s : supporto
def reduce(k,v):
supp = 0
# passo ottimizzabile
for local_sup in v:
supp += local_sup
if supp > s:
return (k, supp)
2.4 Algoritmo di Toivonen
L'algoritmo di Toivonen introduce il concetto di frontiera negativa. Il processing può essere fatto come nel random sampling o come nel SON, l'unica cosa che varia è la selezione dei candidati: oltre a considerare i candidati confrontando il conteggio con un supporto locale, il che potrebbe introdurre falsi negativi (potenziali candidati non rilevati), si considerano i candidati che stanno nella frontiera negativa.
Un itemset sta nella frontiera negativa se e solo se non è frequente e tutti i suoi sottoinsiemi sono frequenti.
Si può dimostrare che introdurre il concetto di frontiera negativa da un contributo importante nell'individuazione di veri positivi tra i candidati, mentre aumenta di poco il numero di falsi positivi.
2.5 Rappresentazioni compatte
Tra i fattori che influenzano la complessità della ricerca di itemset frequenti vi sono:
- La scelta del supporto minimo
- Numero di items (grosse strutture per il conteggio)
- Dimensione del dataset
- Larghezza media delle transazioni
Nell'esempio sottostante abbiamo che, dato l'insieme frequente , tutti i sottoinsiemi (ovvero l'insieme delle parti, meno che l'insieme vuoto) sono anch'essi frequenti e tutti con lo stesso supporto. Vediamo come comprimere l'analisi andando a sacrificare l'informazione fornita dal supporto.
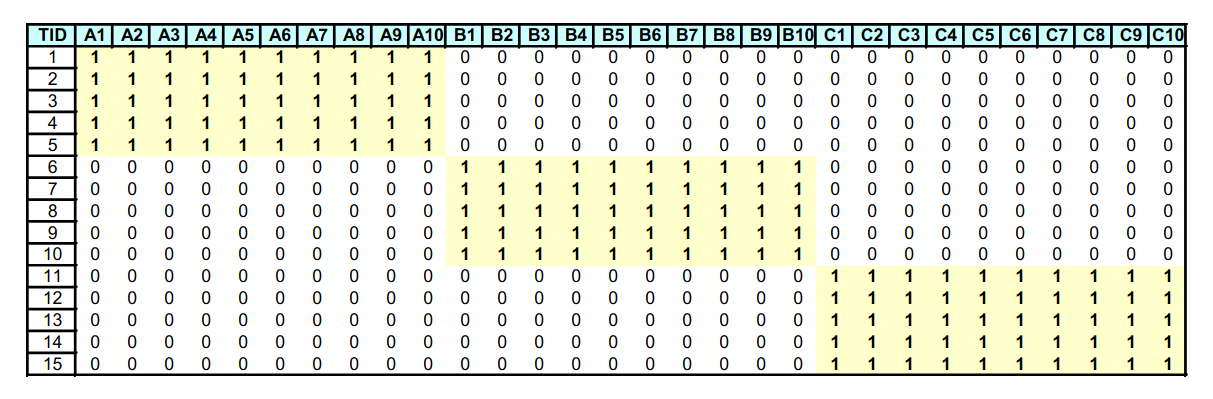
2.5.1 Insiemi frequenti massimali
Osserviamo il seguente lattice:
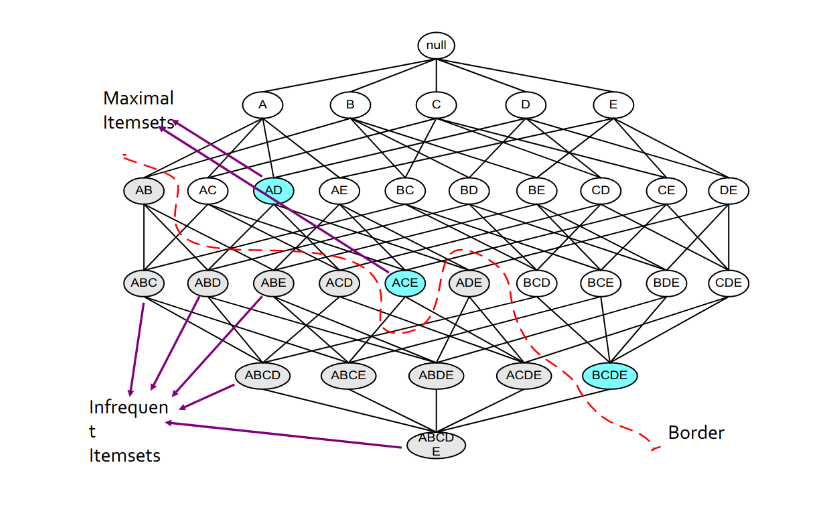
La frontiera rossa separa gli insiemi frequenti (colore bianco) dagli insiemi non frequenti (colore grigio). Gli insiemi colorati in azzurro sono insiemi frequenti massimali. Un insieme frequente si dice massimale quando ogni suo superinsieme (insieme che lo contiene) non è frequente.
Conservando solo gli insiemi massimali trasportiamo una importante informazione: l'insieme delle parti (power set) di un insieme frequente massimale è formato da soli insiemi frequenti. Ovviamente, mantenendo solo gli insiemi frequenti massimali, si perde il supporto dei sottoinsiemi frequenti, che potrebbe essere maggiore. Di conseguenza, mantenere solo gli insiemi frequenti massiamali equivale ad una compressione con perdita (lossy).
2.5.2 Insiemi frequenti chiusi
Se non si è disposti a perdere una informazione preziosa come il supporto, è possibile conservare solamente gli insiemi frequenti chiusi: si definisce insieme frequente chiuso, un insieme frequente quale ogni superset, quindi ogni insieme formato a partire da esso, ha un supporto minore.
Conservando ogni insieme chiuso, sappiamo ogni insieme facente parte del suo power set ha lo stesso identico supporto. Non essendoci perdita di informazione, mantenere solo gli insiemi frequenti chiusi equivale ad una compressione senza perdita (lossless). Tuttavia, il numero di insiemi chiusi è spesso maggiore del numero di insiemi massimali.
Supponiamo che nell'esempio il supporto minimo sia 2:
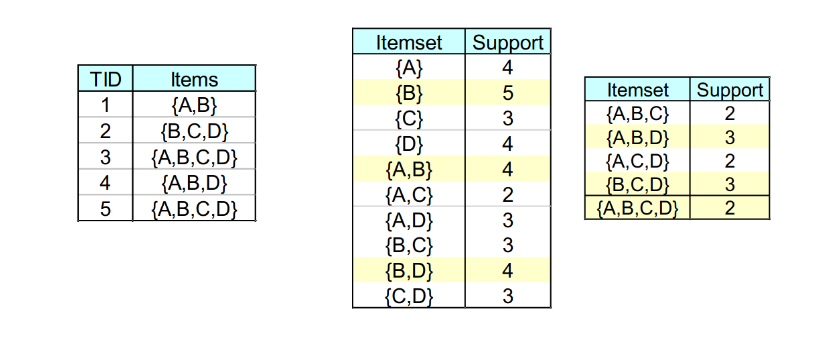
Gli insiemi evidenziati in giallo sono insiemi frequenti chiusi (o lo sono parzialmente). ha un supporto maggiore di , quindi va conservato comunque. Tuttavia, ha lo stesso supporto di , quindi può essere scartato e derivato in seguito come membro del powerset di quest'ultimo.
Gli insiemi massimali sono un sottoinsieme degli insiemi chiusi, che a loro volta sono un sottoinsieme degli insiemi frequenti.
2.6 Generazione dei candidati
L'algoritmo Apriori, e tutti i suoi derivati, attraversarno il lattice con una visita in ampiezza (prima gli itemset di cardinalità , poi quelli di cardinalità , etc). La visita in ampiezza può essere condotta in vari modi:
- General-to-specific: bottom-up, incrementando la dimensione degli itemset
- Specific-to-general: top-down, spezzattando progressivamente gli itemset
- Bidirectional: proseguendo in entrambe le strade contemporaneamente
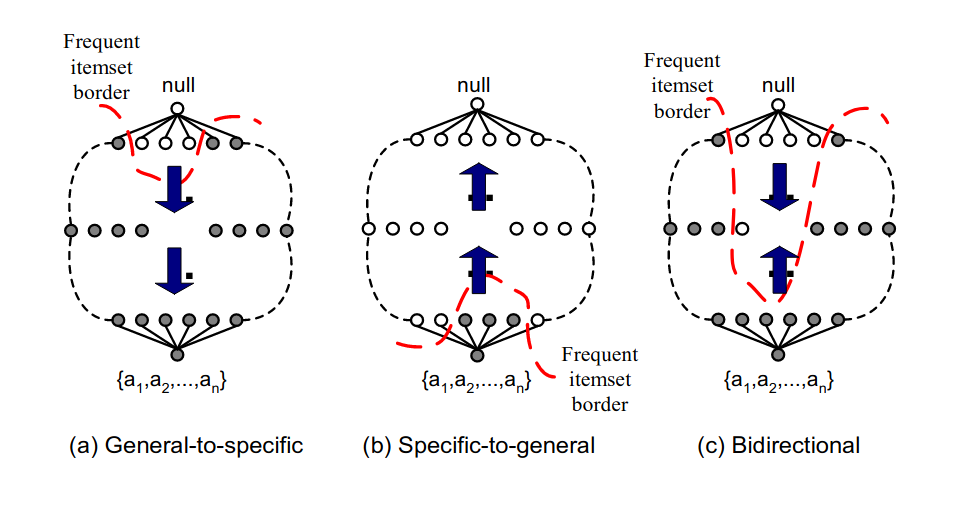
Inoltre è possibile pensare ad una visita in profondità per la generazione dei candidati, come vediamo in esempio:
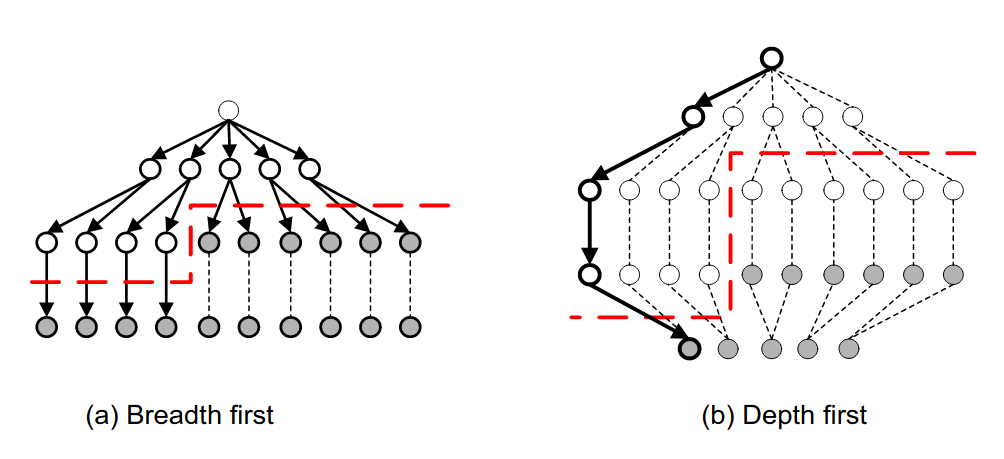
O ancora, anziché utilizzare il lattice completo, costruire un prefix-tree o un suffix-tree, dividendo gli itemset in classi di equivalenza. Così facendo, si riducono le strade da percorrere: nel caso del prefix-tree, dal nodo si diramano tutti i possibili itemset che iniziano per , mentre dal nodo si diramano tutti gli itemset che iniziano per e che non contengono , poiché questi ultimi saranno presenti nel sottoalbero di .
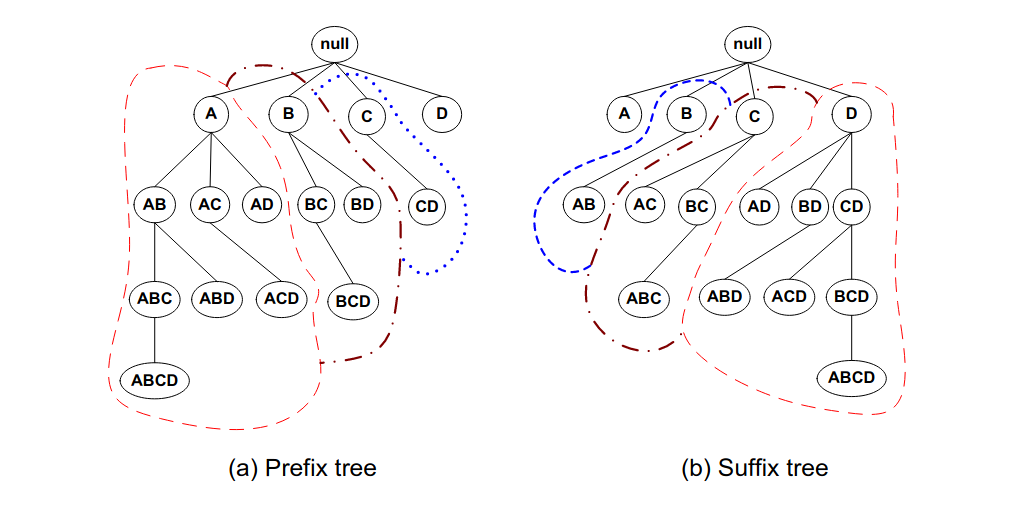
2.6 Database invertito e cenni di ECLAT
Abbiamo sempre considerato il database delle transazioni come una tabella contenente da una parte l'ID della transazione, e dall'altra gli item contenuti. È possibile utilizzare un indice invertito per rappresentare la stessa cosa: costruiamo una tabella avente, per ogni item, le transazioni che lo contengono (TID-list). Per capire se un itemset è frequente, basterebbe intersecare TID-list degli item contenuti e confrontare la cardinalità con il supporto minimo.
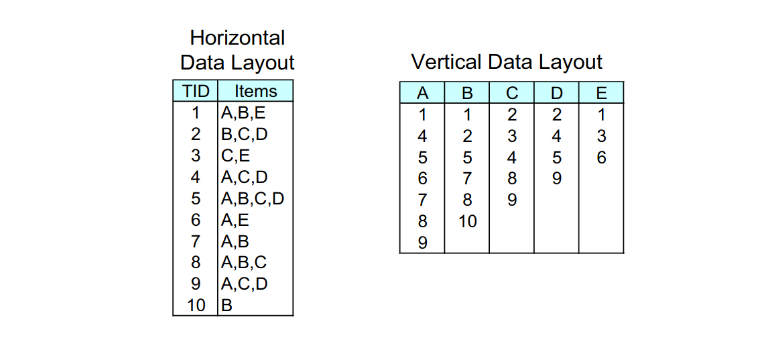
Nell'esempio, per sapere se è frequente basta intersecare l'insieme delle transazioni di con quello di . Se il numero di transazioni in comune è maggiore del supporto, allora l'itemset è frequente.
2.6.1 ECLAT
L'algoritmo ECLAT (Equivalence Class Clustering and bottom-up Lattice Traversal) determina il supporto di un qualsiasi -itemset intersecando le TID-list di due sottoinsiemi qualsiasi di dimensione .
2.7 FP-growth
Il FP-growth (Frequent-Pattern growth) è un algoritmo di estrazione degli insiemi frequenti che utilizza una rappresentazione compressa del database sfruttando un FP-tree. Una volta costruito il FP-tree, l'algoritmo utilizza un metodo ricorsivo divide-and-conquer per rilevare gli insiemi frequenti. Il vantaggio principale del FP-growth è che non è necessaria la generazione dei candidati. Inoltre, non sarà necessario scannerizzare più volte il database per conteggiare gli itemset, in quanto può essere fatto direttamente dal FP-tree in maniera efficiente.
2.7.1 Costruzione del FP-tree
Step 1: Per ogni transazione, si rimuovono gli item con frequenza inferiore al supporto minimo, dopodiché si ordinano i rimanenti in ordine decrescente rispetto al loro supporto.
Nell'esempio visto a lezione, lo step 1 non esiste. Semplicemente le transazioni sono già ordinate.
Step 2: Per ogni transazione, si mappano gli item nell'albero: per ogni item, se dalla radice non vi è nessun figlio contenente il nodo, allora si crea un altro nodo figlio e si inizializza il contatore ad 1. Se esiste, si incrementa di 1 il contatore, si scende al nodo e si prosegue con il prossimo item.
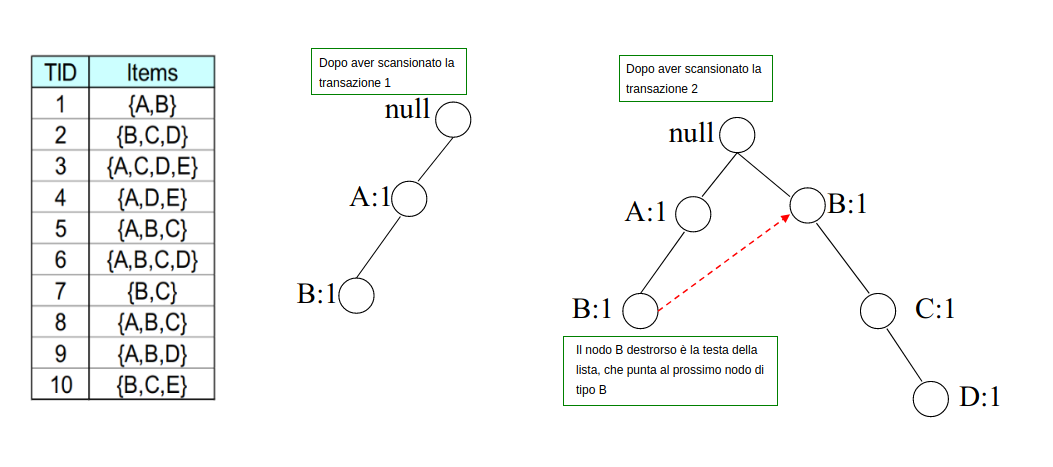
Per ogni item unico si tiene una linked-list che parte dal nodo destrorso nell'albero, che linka al successivo nodo , e così via. Inoltre, una header table contiene i puntatori alle teste (head) di tutte le linked-list. In questo modo risulta semplice trovare nell'albero tutte le occorrenze di itemset contenenti un certo item.
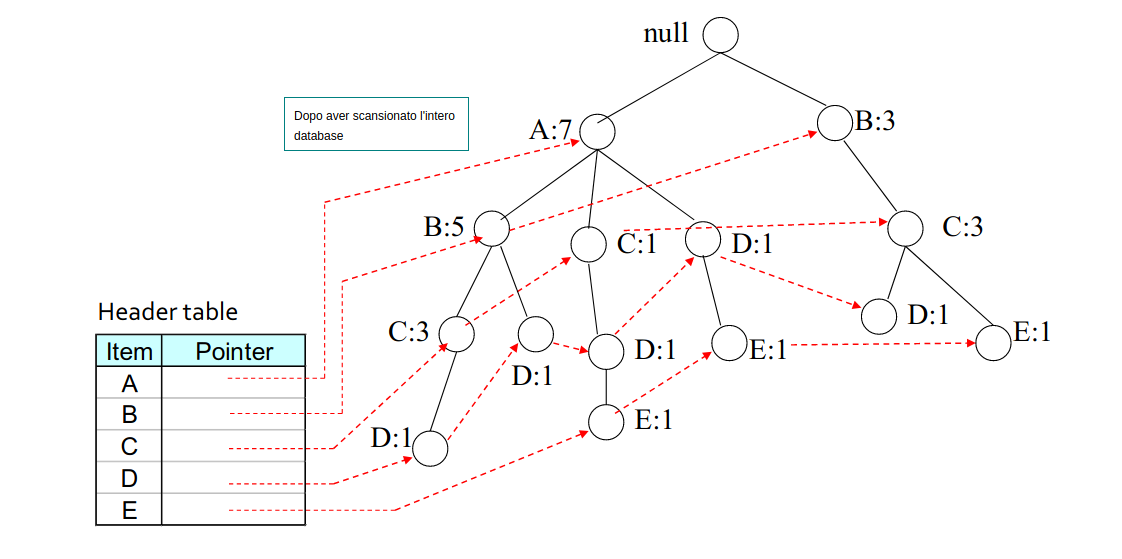
2.7.2 Costruzione dei pattern condizionali
Partiamo dalla fine della header-table e costruiamo il pattern condizionale per . Evidenziamo solo i cammini che finiscono per ed effettuiamo il pruning di tutto il resto.
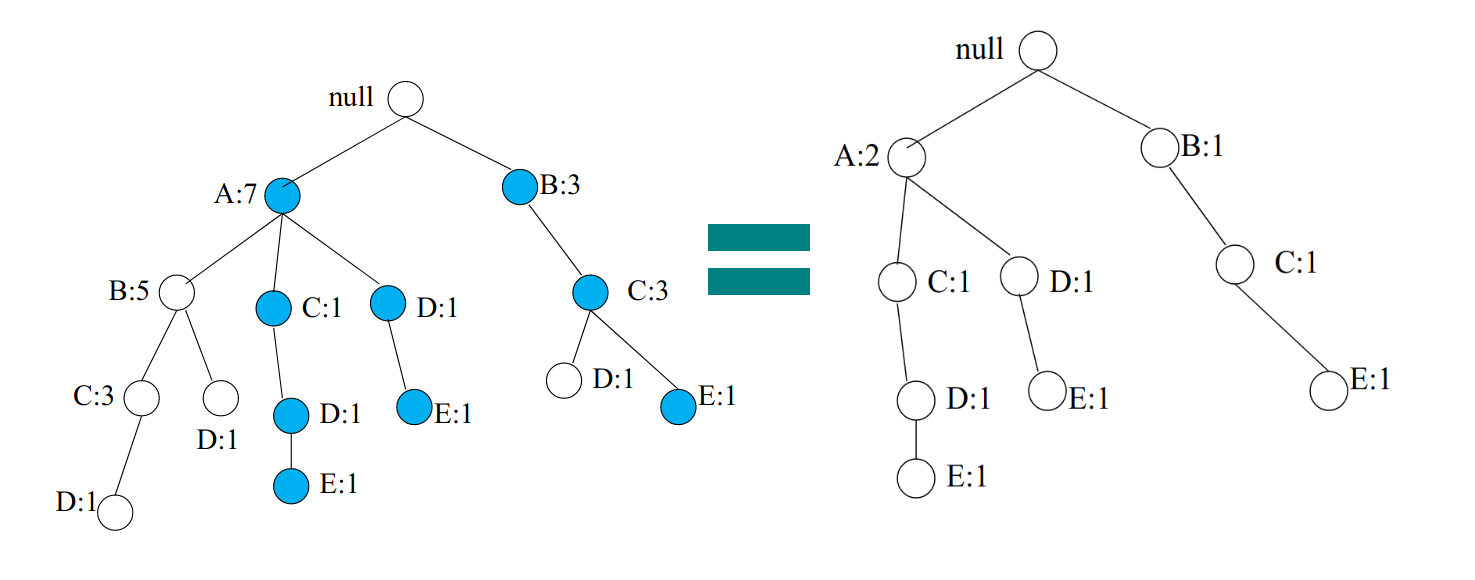
Osserviamo che viene ricalcolato il conteggio sulla base di : il conteggio di è adesso 2, poiché partecipa a 2 cammini che coinvolgono . Costruire l'albero condizionale per è analogo a ricostruire un FP-tree considerando come transazioni solo i cammini che finiscono per . Il conteggio di è 3, per cui se supponiamo che , allora diciamo che è un itemset frequente. Consideriamo l'albero condizionale di ed applichiamo ricorsivamente la stessa procedura con :
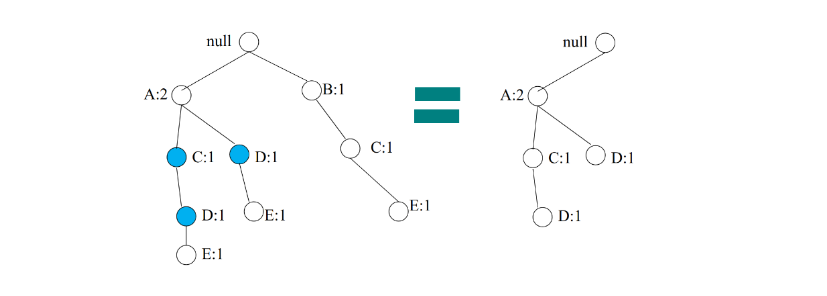
I pattern condizionali per sono: Il conteggio è 2, per cui anche risulta essere frequente. Applichiamo ricorsivamente la procedura per analizzando i pattern per :
È presente un solo cammino, quindi il count per equivale ad 1 (non frequente), quindi lo rigettiamo. Proviamo con :
Il conteggio di vale 2, quindi l'insieme è frequente. Abbiamo completato la ricerca degli insiemi frequenti per , adesso la procedura va ri-eseguita sull'item e così via.
2.7.3 Il metodo frequent pattern growth
Ricapitolando, l'idea è quella di estendere i pattern frequenti. Il metodo consiste nei seguenti passi:
- Per ogni item frequente, costruire la sua base dei pattern condizionali, dopodiché il suo FP-tree condizionale.
- Si ripete il processo su ogni FP-tree condizionale generato sino a quando esso non risulta vuoto.
2.7.4 Scalare il FP-growth
Se il FP-tree non entra in memoria, è necessario adottare delle tecniche per rendere l'algoritmo scalabile. La tecnica adoperata è la DB projection (proiezione del database): si partiziona il database in un insieme di database proiettati, dopodiché si costruisce un FP-tree per ogni database proiettato e si esegui il mining.
Se gli item sono e l'item su cui proiettare il database è , allora la proiezione è fatta come segue: si considerano gli item con cui è possibile estendere , e si scrive . Dopodiché si effettua l'intersezione tra ogni carrello nel database e l'insieme . Il database risultante ha una dimensione minore.
Le proiezioni possono essere fatte su tutto il database (parallel projection) per ogni item frequente oppure si può partizionare il database in base alle proiezioni (partition projection), il che risulta non essere ridondante (link al paper).
2.8 Multiple Minimum Support
Molti dataset reali hanno una distribuzione ripida del supporto dei propri item. Se il supporto minimo è troppo alto potremmo perdere alcuni itemset che includono item rari, mentre se è troppo basso il costo computazionale risulta troppo alto. Una idea è quella di applicare diversi supporti minimi in base all'item (o alla categoria), da questa idea prende il nome di multiple minimum support.
2.8.1 Perdita dell'anti-monotonicità
Esempio, sia il supporto minimo per l'item :
Ipotizziamo di star analizzando il supporto dell'itemset , quale supporto minimo dovremmo utilizzare? La risposta è il supporto minimo più piccolo. Quindi: Problema: il supporto non è più anti-monotono! Supponiamo che:
-
- in questo caso il supporto minimo più basso è quello di , ovvero , quindi l'itemset non è frequente.
-
- il supporto minimo più piccolo è quello di , ovvero , quindi l'itemset è frequente, tuttavia contiene un itemset non frequente al suo interno.
2.8.2 Soluzione - MS Apriori
Si ordinano in maniera crescente gli item in base al loro supporto minimo, basandoci sull'esempio precedente avremo: Sarà necessario modificare l'algoritmo Apriori come segue:
- sarà l'insieme degli item frequenti
- Ogni item è filtrato in base al proprio supporto minimo
- Per si prenderà il supporto minimo più piccolo nell'itemset
- sarà l'insieme di item il cui supporto è (supporto minimo più basso)
- Se un item non supera il supporto minimo più piccolo allora di sicuro non supererà gli altri supporti.
- potrebbe (spesso lo è) più grande di
- è il set di coppie candidate generate da anziché .
Procedura
Ordiniamo gli item in in maniera crescente sulla base del supporto minimo .
- for (, , ) do:
- Se allora
- Altrimenti
- per ogni transazione nel database
- per ogni candidato in
- per ogni candidato in
- return
Notiamo che, dato che viene ordinato con , allora indica il supporto minimo più basso nell'itemset .
2.9 Rule generation
Dopo aver trovato gli itemset frequenti, è necessario generare delle regole. Una regola di associazione è una regola del tipo , e si interpreta come: "Se il carrello contiene , conterrà anche ". Definiamo la confidenza della regola come segue: Sia un itemset frequente, si trovino tutti i sottoinsiemi propri tali che la confidenza della regola superi la soglia di confidenza minima. Se allora vi saranno candidati (conteggiamo i membri del powerset escludendo l'insieme vuoto e l'insieme stesso).
2.9.1 Generazione efficiente di regole
In generale, la confidenza non è anti-monotona, quindi può essere maggiore o minore di . Tuttavia, osserviamo un fatto: consideriamo la regola e calcoliamo la confidenza: Ora spostiamo la al membro di destra: Dalla anti-monotonia del supporto possiamo asserire che: Da cui proviene il teorema:
Se una regola non soddisfa la soglia minima di confidenza, allora qualsiasi regola , dove , non soddisferà la soglia minima di confidenza.
È quindi possibile effettuare pruning nel lattice delle regole di associazione: se non supera la soglia di confidenza minima, allora le regole , , (etc.) non soddisferanno la soglia minima di confidenza.
2.9.2 Pattern evaluation
Esistono molte metriche per validare la valenza di una regola di associazione. Possono essere utilizzate per effettuare un pruning nel post-processing, o in altri casi, un pruning online.
Tavola di contingenza
La tavola di contingenza è una tabella da cui vengono calcolate varie metrice. È definita come segue:
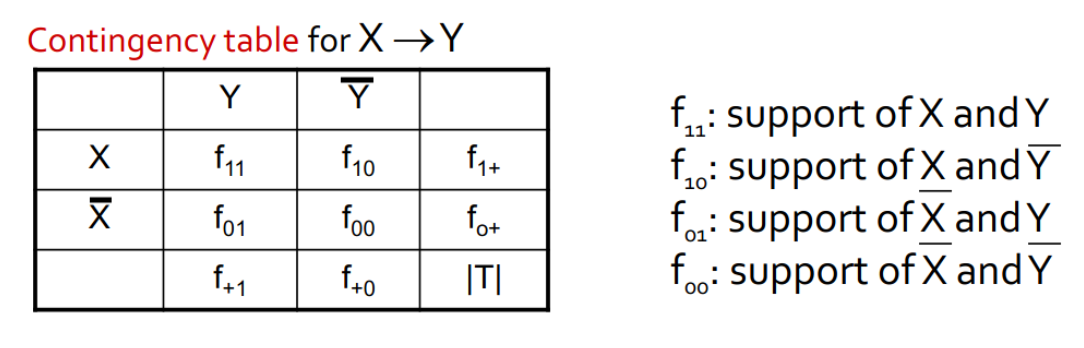
Drawback of confidence
Analizziamo la seguente tabella di contingenza:
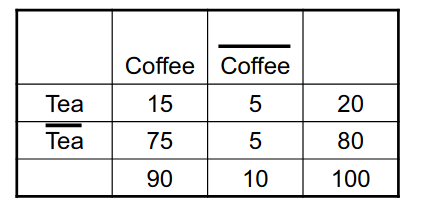
Analizziamo la regola . La confidenza è pari a: Possiamo codificare il fatto in termini di probabilità condizionata, quindi scriveremo che la probabilità . Osserviamo due fatti:
Quindi la probabilità che, non comprando il Te, si compri il caffè è ancora più alta della regola studiata in precedenza, per cui possiamo concludere che: pur avendo una buona confidenza, la regola risulta ambigua e poco interessante.
Ulteriori metriche
- Lift, definito come
- Interest, definito come
- PS (Piatetsky-Shapiro's), definito come
- -coefficient, definito come
E molte altre.
3. Dimensionality reduction
3.1 Introduzione
Molte fonti di dati possono essere viste come matrici di grandi dimensioni (web, social network [matrici di adiacenza], sistemi di raccomandazione [matrice di utilità]). Una matrice può essere riassunta da matrici di dimensione minore, con cui è più efficiente effettuare operazioni. Queste vengono ricavate con metodi di riduzione della dimensionalità. Si effettua riduzione della dimensionalità poiché alcune feature possono risultare irrilevanti, poiché vi è necessità di visualizzare i dati ad alta dimensionalità o poiché la dimensione intrinseca può essere inferiore al numero di feature.
3.1.1 Unsupervised feature selection
Nella feature selection supervisionata vengono selezionate le feature più interessanti rispetto ad una certa etichetta di classe. La dimensionality reduction può essere considerata una feature selection non supervisionata, poiché non si basa su etichette di classe, anche se le feature non vengono selezionate, bensì vengono definite in funzione di quelle originali.
3.1.2 Visualizzazione della riduzione
Supponiamo di avere dei punti distribuiti in uno spazio di dimensione . Può capitare che i punti cadano tutti vicini (o direttamente su) uno spazio a dimensione minore . In questo caso gli assi del sottospazio sono l’effettiva rappresentazione dei dati.
3.1.3 Richiami di algebra lineare
- Il rango di una matrice è un numero intero non negativo associato alla matrice . Ne indica il numero di righe (o colonne) linearmente indipendenti, ovvero non ricavabili attraverso combinazioni lineari di altre righe (o colonne).
- Si dice base di uno spazio vettoriale un insieme di vettori grazie ai quali possiamo ricostruire in modo unico tutti i vettori dello spazio mediante combinazioni lineari. Disponendo di una base di uno spazio vettoriale conosciamo quindi, automaticamente, l'intero spazio vettoriale.
- Si dicono coordinate (o componenti) di un vettore rispetto a una base gli scalari mediante cui il vettore si esprime come combinazione lineare dei vettori della base. Equivalentemente, fissata una base di uno spazio vettoriale, le coordinate di un vettore rispetto alla base scelta sono i coefficienti della combinazione lineare con cui si esprime il vettore in termini degli elementi della base.
- Sia una matrice quadrata. Sia una costante ed un vettore colonna non-zero con lo stesso numero di righe di . Diciamo che è un autovalore di ed è il suo corrispondente autovettore di se . La coppia prende il nome di autocoppia.
- Se è un autovettore di con autovalore e è una qualsiasi costante, allora anche è un autovettore di con lo stesso autovalore . Moltiplicare il vettore per una costante cambia il suo modulo ma non la sua direzione. Per evitare ambiguità assumeremo che ogni autovettore sia un vettore unitario (unit vector), ovvero di modulo 1.
- Sia una matrice quadrata con autovalori e corrispondenti autovettori . Se succede che allora chiameremo autovalore principale
3.1.4 Esempio pratico
Supponiamo di avere in input la seguente matrice A La matrice è bidimensionale, questo poiché è rappresentabile a partire dalla base Se si volesse ricostruire la quarta riga, sarebbe possibile sfruttare una combinazione lineare dei vettori (generatori) della base: Il rango della matrice è quindi l'effettiva dimensione (intrinseca) della matrice. Facciamo un altro esempio: La terza riga è ottenibile dalla differenza tra la prima e la seconda riga, per cui non è linearmente indipendente. Questo vuol dire che il rango è minore di 3. Determinato il rango , indichiamo una nuova base per la matrice: Ed otteniamo delle nuove coordinate per le tre righe: I vettori della base sono gli assi di rappresentazione dei dati, per cui possiamo rappresentare i dati come coefficienti di tali vettori e lavorare su dimensioni minori (2 anziché 3). Per ritornare da coordinate alla base di partenza è sufficiente calcolare la combinazione lineare .
3.1.5 Idea principale
L'obiettivo della dimensionality reduction è proprio quello di identificare gli assi dei dati. Molto spesso i dati non giacciono esattamente su una dimensione minore, per cui è necessario ammettere un margine di errore. Dato un insieme di punti in uno spazio -dimensionale, l'idea principale è quella di proiettare i dati in uno spazio con meno dimensioni preservando quanta più informazione possibile. Scegliamo la proiezione che minimizza il quadrato dell'errore quando ricostruiamo i dati originali.
3.2 Calcolo di autovalori ed autovettori
Nei richiami di algebra lineare abbiamo scritto che, per ogni autocoppia si ha che: Possiamo riscrivere l'equazione nel seguente modo:
Dove è una matrice identità delle stesse dimensioni di . Tale equazione in forma matriciale è rappresentabile come un sistema di equazioni lineari. La matrice corrisponde alla matrice la cui diagonale è ridotta di una fattore . Sia incognita, vogliamo trovare gli autovalori e gli autovettori della matrice .
Affinché si risolva l'equazione per un vettore , il determinante della matrice deve essere diverso da 0. Ciò è necessario poiché se allora per il teorema di Cramer il sistema lineare ammette una sola soluzione, che è banalmente (ma vogliamo una soluzione ). Sebbene il determinante di una matrice abbia termini, questo può essere calcolato in diversi modi in tempo , di seguito vedremo uno tra questi metodi.
3.2.1 Chiò pivotal condensation
Il metodo Chio pivotal condensation (condensazione pivotale) permette di calcolare il determinante di una matrice di dimensione andando a dividere il determinante di una nuova matrice di dimensione per il primo elemento della matrice elevato ad : Ipotesi necessaria è che la diagonale della matrice sia non nulla, quindi che . La matrice va costruita in funzione della matrice . Il generico elemento è ottenuto come segue: Si applica ricorsivamente il metodo alla matrice sino a che non si arriva ad una matrice il quale determinante è trattabile con metodi diretti.
3.2.2 Risolvere l'equazione
Dato che il determinante della matrice è un polinomio di grado dove è l'incognita, allora possiamo ottenere soluzioni, ovvero ottenere tutti ed gli autovalori della matrice . Un valore qualsiasi tra queste soluzioni risolverà l'equazione .
Per ogni autovalore trovato, è possibile ricavare il corrispondente autovettore risolvendo il sistema lineare di equazioni in incognite, ovvero le componenti dell'autovettore : Per semplicità imponiamo che ogni autovettore sia unitario, trovando così una sola soluzione. Facciamo un esempio banale: Quindi impostiamo l'equazione: Risolvendo la sottrazione all'interno delle parentesi otteniamo: Il determinante di questa matrice deve essere 0 poiché il sistema lineare abbia soluzioni: Risolvendo il polinomio di grado troviamo i due autovalori: Prendiamo la soluzione e sostituiamola all'equazione precedente: Ovvero: Risolviamo il sistema lineare ed otteniamo le componenti dell'autovettore associato all'autovalore . Ripetiamo il processo con l'autovalore .
3.2.3 Power iteration
Nella pratica, per matrici molto grandi, la soluzione precedente non è ammissibile. Studiamo un metodo alternativo computazionalmente meno oneroso, chiamato power iteration. Sia una matrice di dimensioni per la quale desideriamo calcolare le autocoppie.
Partiamo da un vettore generato casualmente di dimensione . Calcoliamo un nuovo vettore come segue: dove con intendiamo la norma di Frobenius: Osserviamo che, così facendo, il vettore sarà normalizzato ad 1. Procediamo iterativamente calcolando il generico vettore (per ) come segue: Fissato arbitrariamente un valore costante piccolo , l'iterazione si fermerà quando A questo punto, è approssimativamente l'autovettore principale di . Calcoliamo l'autovalore corrispondente attraverso la formula inversa: Utilizzando questo metodo ricaveremo la prima autocoppia principale (oss. è l'autovalore più grande). Per calcolare le rimanenti autocoppie è necessario enunciare il seguente teorema.
3.2.4 Generalizzazione della Power iteration
Sia una matrice simmetrica di dimensione con autovalori e autovettori. Supponiamo di aver calcolato l'autocoppia principale attraverso la power iteration. Per trovare la seconda autocoppia, creiamo una nuova matrice: Applicare la power iteration alla matrice restituirà l'autocoppia principale della matrice , ovvero l'autocoppia con autovalore più grande. Tale autocoppia corrisponde alla seconda autocoppia della matrice di partenza. Intuitivamente, quello che abbiamo fatto è stato rimuovere l'influenza dell'autovettore principale impostando il corrispondente autovalore principale a zero. Ciò viene giustificato dalle seguenti osservazioni:
- è ancora un autovettore di ed il suo autovalore corrispondente è .
- se è una autocoppia (non principale) di una matrice simmetrica allora sarà una autocoppia di .
È possibile trovare tutte le autocoppie ripetendo iterativamente il metodo:
Osservazione: Se gli autovettori non sono unitari, allora non sarà possibile calcolare la matrice B con l'espressione indicata, bensì si dovrà trovare un vettore tale che e quindi calcolare la matrice B come segue:
Il professore sostiene che l'autovettore ottenuto dalla power iteration su , che chiameremo non corrisponda all'autovettore su , che chiameremo , e che per calcolare l'autovettore originale bisogna applicare la seguente formula:
3.2.5 Implementazione
import numpy as np
import numpy.linalg as la
def powi (m, max_iter = 10 ** 3):
""" power iteration method """
_, n = m.shape
x = np.ones(n)
for _ in range(max_iter):
mx = np.dot(m, x)
fn = la.norm(mx, 'fro')
x = mx / fn
x = x.A[0]
ev = np.dot(np.dot(x.T, m), x).item(0)
return ev, x
def eigenpairs(m):
""" power iteration generalization for all eigenpairs """
_, n = m.shape
b = m
evecs = []
evals = []
for i in range(n):
lambdai, ei = powi(b)
evecs.append(ei)
evals.append(lambdai)
eim = np.matrix(ei)
b = b - lambdai * eim.T.dot(eim)
return evals, evecs
def main():
m = np.matrix([
[1,3,5],
[2,4,1],
[6,1,9],
])
eigen_values, eigen_vectors = eigenpairs(m)
for key, val in enumerate(eigen_values):
print(f'{key}) \t {val}')
3.2 PCA - Principal-Component Analysis
La Principal-Component Analysis (PCA) è una tecnica che prende un dataset relativo ad un insieme di tuple in uno spazio ad alta dimensione e trova le direzioni (assi) lungo il quale le tuple si allineano meglio. Trattiamo l'insieme di tuple come una matrice e troviamo gli autovettori di o . La matrice di questi autovettori può essere pensata come una rotazione rigida dello spazio ad alta dimensione.
3.2.1 Esempio illustrativo
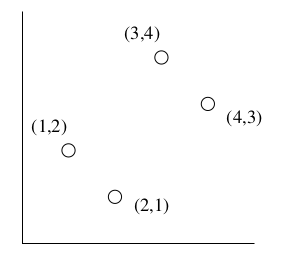
Rappresentiamo i dati nell'asse su una matrice : Calcoliamo il prodotto matriciale Troviamo gli autovalori come fatto nel paragrafo 3.2.2 Le cui soluzioni sono e . Troviamo gli autovettori risolvendo l'equazione lineare per ogni autovalore:
Costruiamo la matrice affiancando gli autovettori trovati e posizionando per primo l'autovettore principale: Ogni matrice con vettori ortonormali (vettori unitari ed ortogonali l'un l'altro) rappresenta una rotazione e/o riflessione degli assi di uno spazio Euclideo. Se moltiplichiamo la matrice per la matrice (rotazione) otteniamo: Nel caso in esempio, la matrice rappresenta una rotazione di in senso antiorario.
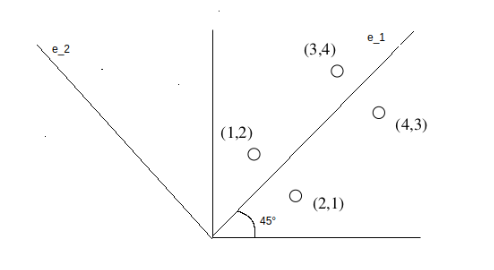
I punti mantengono le proporzioni dopo la rotazione, vediamolo graficamente:
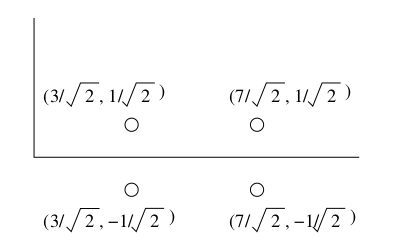
3.2.2 Ridurre la dimensionalità con PCA
corrisponde ai punti di trasformati in uno spazio di nuove coordinate. In questo spazio, il primo asse (quello che corrisponde al più grande autovalore) è il più significativo; formalmente, la varianza di un punto lungo questo asse è la più grande. Il secondo asse corrisponde al secondo autovalore, è il successivo secondo autovalore più significativo nello stesso senso. Questo pattern si presenta per ogni autocoppia. Per trasformare in uno spazio con meno dimensioni, basta preservare le dimensioni che usano gli autovettori associati ai più alti autovalori e cancellare gli altri. Sia la matrice formata dalle prime colonne di . Allora è una rappresentazione di a dimensioni.
Nel nostro esempio, rimuoviamo il secondo autovettore dalla matrice e ricalcoliamo il prodotto : Tale procedura ci garantisce un errore di approssimazione minimo.
3.2.3 Pseudocodice
PCA (M, k):
# Sia M una matrice di dati N x d, con ogni riga un vettore dei dati.
# Otteniamo la matrice di covarianza di M (sottraendo la media)
Sigma <- sottraiamo la media m da ogni vettore riga
autocoppie <- troviamo le autocoppie di Sigma
PC <- prendiamo i k autovettori con gli autovalori più grandi (principal components)
# PC sarà una matrice e gli autovettori saranno posizionati in colonna
return M * PC
3.3 SVD - Singular Value Decomposition
La Singular Value Decomposition (SVD) è una tecnica che permette di ottenere una rappresentazione a basse dimensioni di una matrice ad alte dimensioni e funziona per qualsiasi matrice. Maggiore è la riduzione, minore sarà l'accuratezza della approssimazione.
3.3.1 Definizione di SVD
Sia una matrice , e sia il suo rango. Allora sarà possibile trovare le matrici , , e con le seguenti proprietà:
- è una column-orthonormal matrix, le cui colonne sono vettori unitari (vettori singolari di sinistra).
- è una column-orthonormal matrix, le cui colonne sono vettori unitari (vettori singolari di destra).
- è una matrice diagonale, i cui elementi (nella diagonale) sono chiamati valori singolari di .
Possiamo scrivere:
Per "column-orthonormal matrix" intendiamo una matrice le cui colonne sono vettori ortonormali, per cui il prodotto scalare tra due colonne distinte arbitrarie è 0. Si ha quindi che .
Nella decomposizione si farà utilizzo della trasposta della matrice , quindi . Essendo una column-orthonormal matrix e la sua trasposta, allora sarà una row-orthonormal matrix.
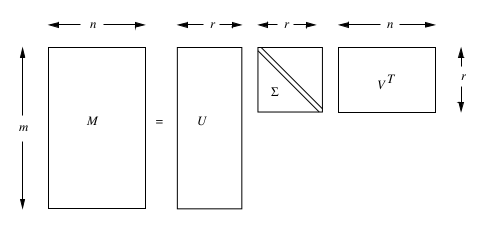
3.3.2 Interpretazione della SVD
Sia una matrice di dimensione contenente nelle righe gli utenti e nelle colonne i film valutati dagli utenti. Supponiamo che i primi 3 film nelle colonne siano fantascientifici, mentre gli ultimi due siano romantici: Le prime 4 righe sono linearmente indipendenti tra loro, così come le ultime 3 righe. Di fatto, il rango della matrice risulta essere . Supponiamo di aver già calcolato le tre matrici , e , scriviamo l'equazione della decomposizione: La chiave di lettura della decomposizione sta nell'interpretare le colonne delle matrici , e come concetti nascosti nella matrice di partenza . Nell'esempio i concetti sono molto chiari, le due colonne indicano i due generi principali: fantascientifico e romantico. La matrice connette gli utenti (righe di ) ai generi (concetti), mentre la matrice connette i film (colonne di ) ai concetti. Infine, la matrice indica la forza di ogni concetto.
L'esempio è particolarmente banale, nella pratica spesso la dimensione desiderata è inferiore al rango della matrice, per cui è necessario applicare alcune modifiche ed ottenere una decomposizione non esatta, ma che approssima al meglio la matrice . È necessario eliminare dalla decomposizione esatta quelle colonne di e che corrispondono ai valori singolari più piccoli (concetti meno affermati) così da ottenere una buona approssimazione.
Modifichiamo leggermente la matrice d'esempio e vediamo cosa succede: Il rango della matrice è adesso a causa delle modifiche: le ultime tre colonne non sono più tutte linearmente indipendenti. Tuttavia i concetti rimangono gli stessi. Vediamo cosa succede alla decomposizione: Il terzo valore singolare risulta molto piccolo rispetto ai primi due, poiché di fatto non è realmente incisivo (nel caso analizzato non indica nessun genere), vorremmo quindi eliminarlo.
3.3.3 Ridurre la dimensionalità con SVD
Supponiamo di voler rappresentare una matrice molto grande attraverso le sue componenti , e ottenute attraverso la SVD. Tuttavia, anche queste ultime risultano essere molto grandi da conservare. Il miglior modo per ridurre la dimensionalità delle tre matrici è azzerare il valore singolare di più piccolo e, di conseguenza, eliminare le corrispondenti colonne nelle matrici e .
Riprendiamo l'esempio precedente: supponiamo di voler passare da 3 dimensioni a 2. Il valore singolare più piccolo risulta essere 1.3, per cui lo azzeriamo e rimuovamo la terza colonna di e la terza riga di : La matrice risultante dal prodotto non coincide perfettamente con , ma ne è una buona approssimazione. Se calcoliamo l'RMSE (root mean square error) attraverso la norma di Frobenius sulla matrice otteniamo: Calcolando l'errore di approssimazione attraverso la metrica RMSE, è possibile dimostrare che ottenuta rimuovendo i valori singolari più piccoli, è la "best low rank approximation" di , ovvero l'approssimazione migliore ottenibile dalle 3 matrici , e .
3.3.4 Best low rank approximation theorem
Sia e dove è una matrice diagonale di dimensioni con: allora è la migliore apporssimazione di rango di , ovvero:
3.3.5 Legami con la decomposizione spettrale
La SVD è legata alla autodecomposizone o decomposizione spettrale di una matrice. Per il teorema spettrale abbiamo che: Dove (diagonale) ed contengono rispettivamente gli autovalori ed autovettori della matrice . Calcolando la SVD di abbiamo: Essendo una matrice diagonale, abbiamo che , continuiamo: In analogia alla decomposizione spettrale, possiamo dire che la matrice contiene gli autovalori della matrice , mentre la matrice ne contiene gli autovettori. Ripetendo lo stesso procedimento con otterremo: Per cui vi è un legame tra le due decomposizioni.
3.3.6 Azzerare i valori singolari piccoli funziona
Dato che , allora
Dato che è di dimensione e è di dimensione , allora il prodotto è una matrice.
Settare (dove è il valore singolare più piccolo) funziona perché essendo e vettori unitari, il prodotto con il valore scala i valori della matrice. Quindi eliminare il più piccolo introduce meno errore di approssimazione.
3.3.7 Quanti valori singolari mantenere
Una regola empirica per scegliere il numero di valori singolari da mantenere consiste nel mantenere almeno l'% (o il %) dell'energia. Ovvero, supponendo che il rango della matrice sia e di voler ridurre la dimensione della decomposizione, allora si sceglie tale che:
3.3.8 Complessità della decomposizione
I migliori algoritmi di calcolo della decomposizione SVD hanno una complessità temporale o , a seconda di quale è minore. Tuttavia vi è meno lavoro necessario se si vogliono ottenere solo i valori singolari (o i primi valori singolari), o se la matrice è sparsa.
3.3.9 Query utilizzando i concetti
Consideriamo la matrice dell'esempio precedente: Supponiamo che un nuovo utente abbia valutato un solo film, il primo, e che lo abbia valutato positivamente. Indichiamo il nuovo utente con il vettore riga . È possibile mappare le valutazioni del nuovo utente nello "spazio dei concetti" moltiplicandolo per la matrice della decomposizione: Dato che la prima componente del vettore risultante vale 2.32, mentre la seconda vale 0, possiamo derivarne che il nuovo utente è interessato a film di fantascienza (la prima categoria), mentre non è interessato a film d'amore. Il vettore risultante è una rappresentazione del vettore delle valutazioni nello spazio dei concetti. Possiamo mappare il vettore nuovamente nello spazio dei film moltiplicandolo per Questo ci suggerisce che il nuovo utente potrebbe essere interessato al secondo ed al terzo film. Un altro tipo di query consiste nel trovare utenti con interessi simili, mappando le loro valutazioni nello spazio dei concetti e calcolando la similarità tra i due vettori attraverso la distanza del coseno, che ci fornisce la differenza delle direzioni dei vettori.
Supponiamo che due vettori delle valutazioni mappati nello spazio dei concetti assumano valori e rispettivamente. I due vettori hanno la stessa direzione: entrambi si trovano sull'asse del concetto "fantascienza", per cui hanno gusti analoghi e la distanza del coseno è 0.
3.3.10 Conclusioni
La SVD è una buona decomposizione grazie al teorema sulla approssimazione low-rank ottimale. Tuttavia è di difficile interpretazione, poiché i vettori singolari specificano combinazioni lineari di colonne e righe di input, e le matrici ottenute non sono sparse, quindi mantenerle in memoria potrebbe essere problematico.
3.4 CUR decomposition
Spesso la matrice da decomporre è molto sparsa. Utilizzando la decomposizione SVD, le matrici , e sono dense. Idealmente si vuole che la decomposizione di una matrice sparsa sia altrettanto sparsa. La decomposizione CUR cerca di garantire questa proprietà. Questo metodo seleziona un insieme di colonne e un insieme di righe che giocano il ruolo di e nella SVD. La scelta delle righe e delle colonne è fatta in maniera casuale con una distribuzione che dipende dalla norma di Frobenius. Tra le matrici ed vi è una matrice quadrata costruita come pseudo-inversa dell'intersezione delle righe e delle colonne scelte.
3.4.1 Definizione di CUR
Sia una matrice di dimensione . Si scelgano concetti da utilizzare nella decomposizione. Una decomposizione di è formata da:
- Una matrice di dimensione formata da colonne prese casualmente da ;
- Una matrice di dimensione formata da righe prese casualmente da ;
- Una matrice di dimensione costruita da ed .
La matrice viene costruita mediante il seguente processo:
- Sia una matrice data dall'intersezione di ed , ovvero l'elemento corrisponde all'elemento di la cui colonna è la -esima colonna di e la cui riga è la -esima riga di ;
- Si effettua la decomposizione SVD su , quindi ;
- Si calcola la matrice pseudoinversa di Moore-Penrose della matrice diagonale , dove ogni elemento della diagonale non nullo si rimpiazza con l'elemento . Se l'elemento della diagonale è nullo, allora si lascia nullo.
- Si ottiene .
Perché la pseudoinversa funziona?
Scomponiamo la matrice utilizzano la SVD , allora deve accadere che . Essendo ed ortonormali, la loro trasposta corrisponderà all'inversa. Quindi scriviamo . Poiché la matrice è diagonale, allora , dove gli elementi in nulli vengono però mantenuti nulli (altrimenti si avrebbe una divisione per zero). Se è non singolare (determinante diverso da zero, di conseguenza esiste l'inversa ) allora la pseudo-inversa coincide con la vera inversa.
3.4.2 Teorema [Drineas et al.]
Sia la decomposizione di calcolata in tempo , allora si dimostra che: Con probabilità , selezionando:
Nella pratica basta selezionare righe e colonne, dove è il valore della "best k-rank approximation" nell'espressione 54, calcolata attraverso la decomposizione SVD azzerando gli valori singolari più piccoli.
Fissati e arbitrariamente, tale teorema ci fornisce il numero di righe e colonne da selezionare per dare un limite superiore all'errore di approssimazione con una certa probabilità.
3.4.3 Selezionare righe e colonne
Anche se la scelta delle righe e delle colonne è casuale, tale scelta deve essere direzionata in qualche modo tale da selezionare le righe e le colonne più importanti. La misura di importanza è data dal quadrato della norma di Frobenius: La probabilità di scegliere la -esima riga di è calcolata come segue: La probabilità di scegliere la -esima colonna di è calcolata come segue: Data la distribuzione di probabilità di righe e colonne, essendo che ogni selezione è indipendente dalle altre, notiamo che le righe con più alta probabilità possono essere selezionate più volte; torneremo più avanti su questo aspetto.
Una volta selezionata con probabilità assegnata una colonna dalla matrice , gli elementi di tale colonna vengono scalati (quindi divisi) di un fattore , la colonna scalata diventa poi una colonna della matrice . Allo stesso modo, selezionata una riga con probabilità assegnata dalla matrice , gli elementi di tale riga vengono scalati di un fatore , quindi la riga scalata diventa una riga della matrice .
3.4.4 Teorema sull'upper bound dell'approssimazione
Ipotizziamo di selezionare un numero analogo di righe e colonne attraverso le distribuzioni di probabilità assegnate dall'algoritmo CUR. Costruiamo quindi le matrici , ed , allora:
3.4.5 Righe e colonne duplicate
La decomposizione CUR è vantaggiosa perché facile da interpretare (i vettori della base sono righe e colonne della matrice) ed inoltre ha una base sparsa. Tuttavia, è possibile riscontrare duplicazioni su colonne e righe a causa della distribuzione di probabilità basata sulle norme: colonne e righe con norme alte verranno selezionate spesso.
Supponiamo che la matrice abbia colonne duplicate, possiamo ridurre queste colonne ad una sola colonna, diminuendo così il numero totale di colonne di . Allo stesso modo, se ha righe duplicate, allora è possibile ridurle ad una sola riga, diminuendo il numero di righe totale di . Tuttavia, tale riga o colonna rimanente dovrà essere scalata moltiplicando ad ogni elemento il valore .
Supponiamo che la matrice di dimensione diventi di dimensione dopo la rimozione dei duplicati. Supponiamo che la matrice di dimensione diventi di dimensione dopo la rimozione dei duplicati. Se il numero di duplicati è diverso in ed () allora la matrice di intersezione non sarà quadrata. Possiamo comunque calcolare la pseudoinversa dalla decomposizione di , dove è una matrice diagonale con alcune colonne o righe nulle (dipeso dalla dimensione maggiore). Si calcola la pseudoinversa canonicamente, e si esegue la trasposizione del risultato. Supponiamo: Allora:
3.4.6 Ottimizzazione dell'algoritmo
Si dimostra che per migliorare l'accuratezza della decomposizione (sulla base della norma di Frobenius), è sufficiente selezionare righe (o colonne) che siano ortogonali (quindi linearmente indipendenti) tra di loro.
3.5 NNMF - Non-negative matrix factorization
Sia una matrice di dimensione , in cui le colonne della matrice rappresentano le osservazioni di un insieme di dati, mentre le righe della matrice sono le corrispondenti feature. La tecnica NNMF ci permette di ottenere una decomposizione: Vogliamo ridurre il numero di feature da a . Le matrici avranno dimensione e . L'interpretazione di , chiamata anche matrice dizionario, consiste nel considerare ogni colonna come un vettore base, quindi un vettore che affiora frequentemente nelle osservazioni.
L'interpretazione di , chiamata anche matrice di attivazione o di espasione, consiste nel considerare ogni colonna come coordinate di una osservazione rispetto alla base . Quindi ci permette di ricostruire una approssimazione dell'osservazione originale attraverso una combinazione lineare delle basi in .
ed sono due matrici con elementi non negativi, ovvero . Il rango della fattorizzazione è scelto in modo tale che ed il prodotto è una rappresentazione compressa di . La non-negatività delle matrici ed induce sparsità.
3.5.1 Definizione di NNMF
Sia . Con indicheremo l'-esima colonna di Sia . Con indicheremo l'-esima colonna di In generale . Il vettore colonna è un vettore base.
Sia . Con indicheremo la -esima colonna di Il vettore colonna corrisponde all'osservazione rappresentata secondo la base formata dai vettori colonna della matrice .
Approssimeremo la feature -esima della -esima osservazione della matrice attraverso il prodotto scalare tra la riga -esima della matrice , che corrisponde all'-esima componente di ogni vettore base, per la -esima colonna della matrice , ovvero la -esima rappresentata attraverso la base .
3.5.2 Legame con Probabilistic Latent Semantic Analysis
Supponiamo che la matrice sia una matrice di co-occorrenza: sulle colonne sono disposti i documenti , sulle righe i termini . L'elemento indica quante volte il termine appare nel documento . Supponendo di introdurre il concetto di topic , quindi tematica trattata da un insieme di documenti, il modello PLSA asserisce che: Ovvero la probabilità di trovare il termine all'interno del documento . Tornando alla decomposizione NNMF, possiamo costruire un modello legato alla PLSA, assumendo che: e anche che quindi possiamo riscrivere il modello come Dove le basi in rappresentano concetti in grado di spiegare i dati analizzati utilizzando i relativi coefficienti in .
3.5.3 Funzione obiettivo
Le matrici e si ottengono minimizzando una certa funzione obiettivo, quindi: Due possibili funzioni obiettivo sono la distanza Euclidea O la divergenza di Kullback-Leibler (KL) Dove con indichiamo il valore stimato di dal prodotto .
3.5.4 Calcolo della NNMF
La NNMF di una matrice può essere calcolata iterando un processo sino a convergenza. Supponiamo di inizializzare le matrici ed in maniera casuale. Ricalcoliamo ad ogni iterazione le due matrici come segue: Dopodiché normalizziamo il risultato: Allo stesso modo calcoliamo la matrice Dopodiché normalizziamo il risultato: Le iterazioni convergono ad un massimo locale della seguente funzione obiettivo, che risulta essere una derivazione della divergenza di KL (in cui si rimuovono i termini costanti):
Assunzione di linearità Nelle decomposizioni affrontate si proiettano linearmente i punti da uno spazio ad un altro, preservando la distanza Euclidea. Altri metodi permettono di effettuare delle proiezioni non lineari (i.e. isomap), in cui i punti ricadono in una curva (manifold) a più bassa dimensione.
4. Sistemi avanzati di raccomandazione
È possibile trovare una introduzione ai sistemi di raccomandazione nel testo Dive Into Data Mining.
4.1 LSI - Latent Semantic Indexing (LSI)
Il LSI è una tecnica sviluppata nei primi anni '90 che risolve il problema della sparsità e scalabilità per grandi dataset nel contesto semantico. Consiste principalmente nel ridurre la dimensionalità e catturare le relazioni latenti su matrici termini-documenti. Questa tecnica di indicizzazione utilizza la decomposizione SVD per identificare pattern nella relazione tra termini e concetti contenuti nel testo: si basa sul principio che parole utilizzate nello stesso contesto tendono ad avere significato simile.
4.1.1 LSI per sistemi di raccomandazione
È possibile applicare la tecnica LSI nel contesto dei sistemi di raccomandazione:
- La matrice termini-documenti sarà sostituita con la matrice di utilità
- Le categorie degli item prenderanno il posto dei concetti
- Il mapping , diviene ,
Quindi si calcola la SVD della matrice : Dalle proprietà della SVD sappiamo che le matrici e sono matrici dense.Sia il vettore contenente tutte le valutazioni effettuate dall'utente sugli item, supponendo che se l'utente non ha valutato l'item , allora . Calcoliamo dove è la matrice di dimensione della decomposizione che rappresenta la corrispondenza film-categorie. Così facendo, mappiamo le valutazioni correnti dell'utente dallo spazio originale a quello delle categorie. Calcoliamo la predizione della valutazione dell'utente su tutti i film come segue
4.2 Metodi Graph-based
I metodi graph-based sfruttano una idea simile a quella del collaborative filtering, ma utilizzano un grafo bipartito per immagazzinare le informazioni. Le raccomandazioni sono ottenute a partire dalla struttura della rete bipartita.
Sia un grafo bipartito, in cui di cardinalità ed di cardinalità sono due classi di identitià indicanti rispettivamente gli utenti e gli oggetti. Sia l'insieme degli archi E una funzione peso che rappresenta il grado di preferenza espresso dall'utente per un particolare oggetto. La utility matrix corrisponde alla matrice di adiacenza del grafo bipartito.
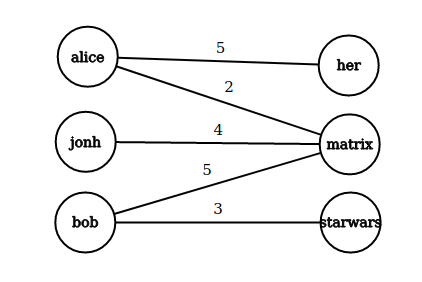
4.2.1 NBI - Network-based inference
La network-based inference è una tecnica sviluppata nel 2007 in cui si effettuano delle proiezioni sul grafo bipartito per ottenere informazioni. Dal grafo definito in precedenza è possibile estrarre due proiezioni: la proiezione rispetto agli utenti e quella rispetto agli oggetti. In una proiezione vi sono nodi appartenenti allo stesso insieme e due nodi sono connessi se e solo se sono connessi ad almeno un nodo in comune dell'altro insieme nel grafo di partenza.
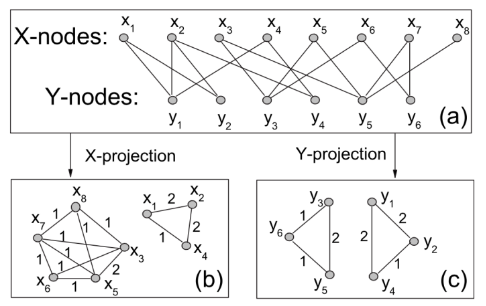
4.2.2 Idea dell'NBI
Sia il grafo bipartito definito in precedenza, definiamo una matrice di adiacenza dove Si esegue un processo di trasferimento delle risorse (resource transfer) tra i due insiemi della rete: all'inizio vengono trasferite delle risorse dall'insieme all'insieme e, successivamente, le risorse tornano da ad . La risorsa contenuta in un nodo viene trasferita equamente ai nodi adiacenti nell'altro insieme. Il processo a due fasi si ripete sino a convergenza. Questo metodo ci permette di definire una tecnica per il calcolo della matrice dei pesi di dimensione di una proiezione di rispetto all'insieme come segue: Quindi iteriamo per tutti gli item in e, se l'item è in comune tra i due utenti e , allora acquisisce valore inversamente proporzionale al grado dell'oggetto. La funzione è arbitraria e definisce il metodo graph-based utilizzato: Per ottenere le predizioni delle valutazioni, ovvero la matrice di raccomandazione , è sufficiente computare il prodotto riga-colonna tra la matrice dei pesi della proiezione del grafo bipartito (sugli utenti), che ha una dimensione , per la matrice di adiacenza del grafo bipartito , che ha una dimensione Il peso della proiezione corrisponde a quante risorse vengono trasferite dall'oggetto all'oggetto , o quanto piacerà l'oggetto ad un utente a cui piace l'oggetto .
Il NBI funziona su tutti i tipi di oggetti e risolve il problema della sparsità della utility matrix. Tuttavia persistono i problemi con i nuovi utenti o i nuovi item ed il metodo richiede importanti risorse computazionali.
4.3 Metodi ibridi
I metodi ibridi sfruttano una combinazione di diversi metodi di raccomandazione, risultando essere dei meta-sistemi. Supponiamo di avere due metodi ed che diano rispettivamente gli score e . Lo score di un modello ibrido può essere ottenuto come: I valori sono normalizzati per lo score massimo che il rispettivo metodo di raccomandazione ha ottenuto. Il modello è generalizzabile per l'utilizzo di sistemi di raccomandazione.
La valutazione dei risultati di un sistema di raccomandazione consiste spesso nel calcolare il root mean square error (RMSE) tra le valutazioni reali dell'utente e le predizioni del sistema. Una alternativa sta nell'interpretare il problema come un task di classificazione binaria, dove con 1 indichiamo una relazione tra utente e item e viceversa con 0. Di conseguenza sarà possibile calcolare metriche come la precision e la recall, o disegnare la curva ROC.
4.4 BellKor Recommender System
Il BellKor Recommender System è il sistema di raccomandazione che ha vinto il Netflix Prize. Combina tre fattori principali: gli effetti globali, la fattorizzazione ed il collaborative filtering.
4.4.1 Introduzione
Il collaborative filtering sfutta un criterio globale ed uno locale per effettuare la predizione finale, di fatto la raccomandazione dell'utente per l'item è ottenuta dalla seguente espressione: Dove con intendiamo la baseline per l'utente rispetto all'item e con intendiamo la similarità tra gli item e . Tale espressione vale nel caso degli item-item CF; nel caso degli user-user CF è sufficiente trasporre la matrice di utilità.
Il criterio globale nell'espressione consiste nell'utilizzo della baseline. La baseline è data dalla somma della media globale delle valutazioni , la deviazione delle valutazioni sul film rispetto alla media, la deviazione delle valutazioni dell'utente rispetto alla media. Quindi . Supponiamo che la media delle valutazioni sia stelle. Il film "Sesto senso" è valutato stelle sopra la media; l'utente Joe valuta i film sotto la media. La baseline estimation del rating di Joe per "sesto senso" è stelle. Tutte le informazioni utilizzate per il calcolo della baseline sono informazioni globali. Attraverso delle informazioni locali ottenute (ad esempio) attraverso il collaborative filtering, è possibile effettuare una predizione più precisa. L'espressione 10 fornisce tutto ciò che serve per il calcolo della predizione finale.
4.4.2 Parametri arbitrari
L'espressione 10 presenta un parametro totalmente arbitrario: la misura di similarità. La similarità influenza in maniera diretta il risultato del sistema, e quindi le dipendenze tra gli utenti (o tra gli item). È possibile sostituire la similarità con dei pesi calcolati attraverso un processo di training. Quindi riscriviamo l'espressione 10 Dove è un peso di interpolazione che modella l'interazione tra gli oggetti (o gli utenti), indipendente dall'utente. Assumiamo che:
4.4.3 Primo problema di ottimizzazione
La matrice di utilità è un dataset contenente dei dati reali, con cui possiamo confrontare i risultati del nostro sistema. Avendo le predizioni e sapendo calcolare la predizione , i pesi saranno l'incognita da trovare. A questo punto si utilizza un algoritmo di ottimizzazione per minimizzare il SSE (sum of square errors) calcolato sui dati di training (n.b. si utilizza il SSE anziché il RMSE poiché la derivata è più semplice).
La objective function da ottimizzare sarà la seguente: Un algoritmo di ottimizzazione possibile è la discesa del gradiente: sia il learning rate, aggiorniamo la nostra matrice di pesi come segue: e ripetiamo sino a convergenza. Anche se nell'espressione è presente il gradiente , in realtà si parla di matrice Jacobiana poiché presenta 2 dimensioni. Nel nostro caso avremo \forall i,x \and j \in N(i;x) , quindi vicino ad , altrimenti avremo:
4.4.4 Fattori latenti
Sia la matrice di utilità, effettuiamo la scomposizione SVD e riduciamo la dimensionalità a fattori latenti, otteniamo: Sia e , allora: Per stimare l'elemento della matrice è sufficiente effettuare il prodotto scalare tra la -esima riga di e la -esima colonna di (o analogamente, la -esima riga di )
4.4.5 Secondo problema di ottimizzazione
La SVD non è applicabile quando nella matrice vi sono elementi non definiti. Tuttavia è possibile ovviare al problema ricavando le matrici e attraverso i metodi di ottimizzazione. Consideriamo la seguente funzione obiettivo (sum of squared errors, SSE): Con indichiamo la -esima riga della matrice , con indichiamo la -esima riga della matrice . Il metodo non richiede che le due matrici siano ortonormali. Sia il numero di fattori latenti, si osserva empiricamente che l'ottimizzazione soffre di problemi di overfitting già per .
Introduciamo la regolarizzazione nella funzione obiettivo basandoci sull'idea che una maggiore quantità di valutazioni permette una predizione più accurata per un determinato utente. Geometricamente, si interpreta posizionando l'utente (vettore di valutazioni) lontano dal centro (quindi predizione più sicura) se il numero di valutazioni effettuate è alto. Nella pratica aggiungiamo il termine tra parentesi quadre: Dove sono parametri che permettono di eseguire un tuning sul peso della regolarizzazione. Anche questa volta è possibile utilizzare l'algoritmo di discesa del gradiente, iterando sino a convergenza ed aggiornando le matrici come segue Dove indica il gradiente (o più correttamente, la matrice jabobiana) della funzione obiettivo rispetto a : Ed analogo il calcolo di .
4.4.6 Stochastic Gradient Descent
Il calcolo del gradiente nell'algoritmo di discesa del gradiente è particolarmente oneroso, supponiamo di stare effettuando l'ottimizzazione per un regressore lineare : Supponiamo che la funzione obiettivo sia definita come segue Quindi lo step di aggiornamento dell'algoritmo di discesa del gradiente sarà: Ovvero per ogni coefficiente si calcola la derivata parziale della funzione obiettivo sull'intero training set. Se la dimensione del training set è particolarmente grande, i dati saranno molto probabilmente conservati in memoria secondaria. L'algoritmo risulta quindi molto pesante. Supponiamo di definire una funzione costo: Quindi riscriviamo la funzione costo come L'algoritmo di discesa del gradiente stocastico (Stochastic Gradient Descent, SGD) consiste in due step ripetuti in maniera iterativa:
- Permutare casualmente il training set
- Aggiornare i coefficienti come segue
Osserviamo che all'interno dello step di aggiornamento vi è la derivata parziale della funzione costo anziché della funzione obiettivo: questo implica che, ad ogni step, i pesi vengono aggiornati basandosi su una singola osservazione del training set e non su tutti i dati.
Lo stochastic gradient descent è molto più rapido dell'algoritmo di discesa del gradiente classico. Tuttavia, la convergenza ad un minimo locale della funzione obiettivo risulta essere più instabile e necessita di più step.
4.4.7 Costruzione del modello
È possibile combinare il predittore baseline con le interazioni utente-film ottenute attraverso la scomposizione in fattori latenti: Quindi minimizzare la funzione obettivo così proposta In questo caso sia le interazioni e che i bias e sono trattati come parametri da stimare e vengono aggiunti termini di regolarizzazione anche per i bias.
4.4.8 Bias temporali
Una ulteriore miglioria al modello consiste nel legare i bias e ed i fattori e al tempo, sotto la considerazione che la valutazione di un film tende ad essere stabile per i film vecchi ed instabile per i film nuovi.
La soluzione del team "BellKor's Pragmatic Chaos" vincitore del Netflix prize consiste nell'eseguire un blend lineare dei risultati di diversi tipi di predittori (approssimativamente 500) che sfruttano i concetti mostrati, ottenendo un miglioramento del 10.09%.
5. Finding Similar Items
Un problema noto è la ricerca di item simili: supponiamo di voler esaminare le pagine web per cercare casi di plagio. Un approccio naive consisterebbe nel calcolare la distanza di ogni coppia di pagine; tuttavia questo approccio risulta proibitivo nel caso di grandi dataset poiché quadratico.
5.1 Similarità tra insiemi
Supponiamo di rappresentare i documenti (i.e. pagine web) come insiemi. Un modo di calcolare la similarità tra due insiemi e è la similarità di Jaccard, definita come il rapporto tra la cardinalità dell'intersezione e dell'unione dei due insiemi:
Dare una lettura al sottocapitolo 3.1 di 'Mining of massive datasets' di Ullman et al.
5.2 Shingling
Il metodo più efficace per rappresentare insiemisticamente dei documenti, allo scopo di identificare documenti lessicalmente simili, consiste nel creare un insieme a partire dalle stringhe contenute nel testo. Due documenti simili avranno stringhe (es. parole o frasi) simili. Una semplice tecnica per ottenere un insieme da un documento testuale è lo shingling.
5.2.1 -Shingles
Un documento è una stringa di caratteri. Si definisca un -shingle di un documento come una qualsiasi sottostringa di lunghezza nel documento. Dopodiché vengono associati al documento un insieme di -shingles ed (opzionalmente) la loro frequenza assoluta.
5.2.2 Lunghezza dello shingle
Scegliendo un valore troppo piccolo, ci aspetteremo che quasi tutte le sequenze di caratteri siano presenti nella maggioranza dei documenti. Così facendo, ogni coppia di documenti avrebbe una similarità di Jaccard molto alta.
deve assumere un valore grande abbastanza, tale che la probabilità che un qualsiasi shingle appaia in un qualsiasi documento sia bassa.
Nel caso di un corpus di email, dovrebbe funzionare bene: supponendo che si incontrino solo caratteri alfabetici e spazi bianchi, allora avremo shingle. Essendo che una email è molto più corta del numero indicato, la probabilità che uno tra gli shingle appaia nel documento risulta essere bassa.
5.2.3 Hashing shingles
Sia l'insieme dei caratteri possibili in un documento e supponiamo, per semplicità, che essi siano 27. Per abbiamo possibili shingle. Ogni carattere occupa un byte, quindi un intero shingle occuperà 9 byte. Possiamo applicare una funzione di hashing che mappa ogni shingle in un numero tra e : Così facendo, ogni shingle sarà rappresentato da un intero a 4 byte. Lo spazio occupato sarà rispetto alla rappresentazione originale.
5.2.4 Costruire shingle da parole
Supponiamo di osservare una pagina web contenente un articolo con un certo topic. Come distinguiamo le stringhe provenienti dall'articolo dagli altri contenuti della pagina? Si osserva che gli articoli, come la maggior parte dei contenuti scritti in prosa, contengono molte stop words (congiunzioni, articoli, punteggiatura), ovvero parole poco significative nella distinzione del contenuto.
Tuttavia, si è dimostrato empiricamente che la tripla formata da una stop words e le due parole seguenti formano uno shingle molto efficace. In questo modo l'articolo contribuirà di più alla formazione degli shingle e la distinzione sarà basata su elementi provenienti dall'articolo piuttosto che dagli elementi circostanti della pagina web. La similarità di Jaccard sarà più alta per documenti con articoli simili rispetto a documenti con elementi circostanti all'articolo simili.
5.3 Min-Hashing
Gli shingle possibili sono moltissimi e, all'aumentare dei documenti, potrebbe essere impossibile tenere tutto in memoria principale. L'obiettivo principale è quello di sostituire grandi insiemi di shingle con una rappresentazione molto più piccola, chiamata signature (firma). La proprietà più importante che vogliamo rispettare è che, comparando le signature di due documenti, la similarità di Jaccard sia approssimativamente analoga a quella che si otterrebbe comparando i loro rispettivi insiemi di shingle.
5.3.1 Rappresentazione matriciale degli insiemi
Prima di tutto occorre costruire una characteristic matrix. In questa matrice, la -esima colonna rappresenta l'insieme di shingle estratto dal -esimo documento, mentre la -esima riga indica l'-esimo shingle tra tutti gli shingle possibili.
Esempio: supponiamo di avere 100 documenti, 27 caratteri possibili e . Per ogni documento estraiamo l'insieme di shingle. Nella matrice vi saranno 100 colonne (una per l'insieme di ogni documento) e righe (una per ogni possibile shingle).
L'elemento della matrice varrà 1 se lo shingle è contenuto nell'insieme degli shingle del documento , altrimenti varrà 0. Chiamiamo universal set l'insieme di tutti i possibili shingle.
5.3.2 Min-hashing
Le signatures degli insiemi che vogliamo ottenere sono composte dai risultati di centinaia di calcoli, chiamati minash della characteristic matrix. Supponiamo di avere la seguente matrice:
Per calcolare il minhash è necessario effettuare una permutazione delle righe, supponiamo che la prima permutazione sia e riscriviamo la matrice:
Dopodiché utilizziamo una funzione hash su ogni insieme (colonne). Tale funzione ritorna in output la prima riga dell'insieme che presenti un 1:
Quindi il minhash corrisponde a . Questo processo si ripete volte, dove è solitamente molto più piccolo della cardinalità dell'insieme universale. Una volta calcolato il minhash da una permutazione, esso va inserito come riga di una matrice, chiamata signature matrix:
Una volta ripetuto volte il processo con diverse permutazioni, la signature dell'insieme corrisponderà alla colonna -esima della signature matrix. Per semplicità, definiamo una funzione hash (notare l'assenza di permutazione al pedice) che rappresenti il processo di calcolo di una signature a partire da un insieme di shingle .
5.3.3 Min-hashing e Similarità di Jaccard
Vogliamo che valga la proprietà fondamentale per cui: Dove indica una particolare similarità tra signature che corrisponde alla frazione di minhash in cui esse coincidono:
Teorema 1
Si può dimostrare che:
Sia l'insieme di shingle e un elemento dell'insieme, allora:
Dove con indichiamo l'indice di nella permutazione . Possiamo affermare ciò poiché ogni elemento dell'insieme ha equa probabilità di essere primo nella permutazione .
Nota bene: la cardinalità corrisponde al numero di shingle contenuti nell'insieme, ovvero al numero di elementi nella colonna -esima posti ad 1.
Vogliamo studiare la probabilità che si verifichino i due eventi: Quindi che sia l'elemento di indice 1 nella permutazione in entrambi gli insiemi ed (ammesso che vi sia). La probabilità è sempre distribuita uniformemente, ma adesso è necessario considerare che tutti gli elementi dell'unione sono candidati ad essere primi, quindi:
P\left(\pi(y) = h_{\pi}(S_i) \and \pi(y) = h_{\pi}(S_j)\right) = \frac{1}{|S_i \cup S_j |}
Se volessimo trovare la probabilità che il primo elemento sia uguale in entrambi gli insiemi ed , è necessario considerare tutti gli elementi della loro intersezione come possibili candidati, dove ogni elemento ha probabilità uniforme, quindi: Il che dimostra la nostra tesi.
Teorema 2
Per semplicità, abbreviamo: Sia una soglia di similarità al di sopra della quale consideriamo due insiemi di shingle "altamente simili". Supponiamo che sia limitato inferiormente da una costante . Allora vale il seguente teorema:
Siano , , e , allora per ogni coppia di insiemi valgono le seguenti proprietà: Dove e sono parametri arbitrari; il teorema ci permette di limitare il numero di falsi positivi e falsi negativi (controllare l'errore). Dimostriamo la proprietà a) Scriviamo: Banalmente, poiché se l'evento accade con probabilità , allora l'evento complementare o contrario accade con probabilità .
Grazie al teorema precedente, possiamo asserire: Usiamo funzioni hash, quindi permutazioni e definiamo una variabile aleatoria come segue: Con Osserviamo che La variabile aleatoria è distribuita secondo una distribuzione binomiale, . Il valore atteso è noto e corrisponde a: Poiché la similarità originale corrisponde proprio alla similarità di Jaccard.
Sappiamo che la similarità tra signatures corrisponde al numero di volte in cui i minhash corrispondono (casi favorevoli) rispetto al numero di minhash totali, quindi scriviamo: Anche questa è una variabile aleatoria, il cui valore atteso corrisponde a: Quindi la similarità tra signatures è un estimatore corretto della similarità di Jaccard tra gli insiemi. Questo vuol dire che al crescere del numero di funzioni hash applicate, per la legge dei grandi numeri, l'estimatore converge al parametro stimato. Utilizziamo adesso un importante teorema, chiamato Chernoff Bound, che enuncia: Riscriviamo l'espressione dettata dal Chernoff Bound sostituendo i protagonisti e ricordandoci di aver considerato il complementare nell'espressione (17): Per ipotesi, sappiamo che: Quindi possiamo sostituire nella disequazione (26) con la similarità di Jaccard: Essendoci ricondotti al valore atteso di (vedasi espressione 22), è possibile applicare il Chernoff Bound: Fissati e , ricaviamo la quantità (funzioni hash necessarie ad ottenere un certo controllo dell'errore) risolvendo la disequazione: Quindi la proprietà è dimostrata.
5.3.4 Row hashing
Effettuare una permutazione è una operazione molto dispendiosa. Una ingegnerizzazione del min-hashing, chiamata row-hashing, permette di effettuare lo stesso procedimento rapidamente. Supponiamo di avere documenti e funzioni hash del tipo: Dove e sono due interi arbitrari, è un numero primo, è il numero di shingle e si ha che . Sappiamo a priori che la matrice delle signatures avrà dimensione . La procedure consiste nei seguenti passi:
- Inizializzare la matrice delle signatures ad .
- Per ogni riga (termine)
- Per ogni funzione hash
- Generare l'indice della riga nella permutazione data da
- Per ogni documento controllare se all'indice vi è un 1.
- Se è così, allora se l'elemento è maggiore di
- Se è così, allora se l'elemento è maggiore di
- Per ogni funzione hash
Vediamo un esempio: Supponiamo di avere funzioni hash definite come segue: Che generano le due permutazioni: Inizializziamo la matrice delle signatures: La riga della characteristic matrix ha indici nelle permutazioni generate dalle funzioni hash. I documenti ed hanno valore 1 nella prima riga, quindi possiamo aggiornare la matrice delle signatures come segue: La riga della characteristic matrix ha indici e solo il documento ha valore 1, aggiorniamo: La riga della characteristic matrix ha indici ; i documenti ed hanno valore 1, aggiorniamo i valori minori di quelli esistenti nella matrice delle signatures (ad esempio rimane lo stesso poiché e ): Allo stesso modo, per : E per : Abbiamo costruito la matrice delle signatures senza generare effettivamente le permutazioni delle righe di ogni colonna. Questa ingegnerizzazione rende il minhashing molto più rapido.
5.4 Locality Sensitive Hashing
Calcolare la similarità tra ogni coppia di documenti presenti nel database è un task dispendioso e l'approccio naive ha un tempo . Il Locality Sensitive Hashing permette di svolgere il task in tempo lineare controllando l'errore di approssimazione.
L'idea di base consiste nel generare uno sketch per ogni oggetto (nel nostro caso un documento) tale che:
- Sia molto più piccolo rispetto al suo numero originale di feature
- Trasformi la similarità tra due vettori di feature in una operazione di uguaglianza tra sketch
Tale metodologia è randomizzata e corretta con alta probabilità, quindi ammettiamo un certo numero (ragolabile) di falsi positivi e falsi negativi, ed inoltre è ottima in approcci distribuiti.
5.4.1 LSH e Distanza di Hamming
Per spiegare semplicemente il procedimento e le proprietà del LSH, prendiamo in considerazione la distanza di Hamming. Supponiamo di avere due vettori binari e con feature. La distanza di hamming è definita come
D(p,q) = \text{#bits where p and q differ}
Definiamo una funzione hash che prenda un insieme random di feature Ad esempio se , assumendo che allora la proiezione . Definiamo la similarità di Hamming come segue il rapporto tra le feature che combaciano nei due vettori binari e le feature totali: Scegliendo casualmente una posizione nei nostri vettori binari, la probabilità che il valore di e combaci nella posizione è data proprio dalla similarità: Dato che la funzione hash genera un insieme di posizioni random e indipendenti tra loro, la probabilità che e combacino in tutte e le posizioni corrisponde a: Aumentando
- Aumentano il numero di posizioni nell'insieme
- Aumenta la probabilità di trovare posizioni che differiscono nei due vettori binari
- Diminuisce la probabilità che i vettori binari combacino
- Diminuisce il numero di falsi positivi
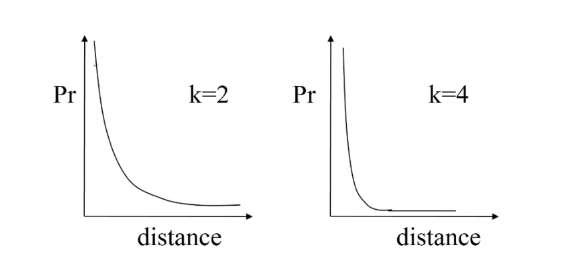
5.4.2 Gestire i falsi negativi
Per ridurre i falsi negativi, l'idea implementata nel LSH sta nel ripetere volte le -proiezioni dei vettori e, ad ogni ripetizione, generare insiemi casuali differenti.
Abbiamo funzioni hash e definiamo la proiezione del vettore binario come Dichiariamo che è simile a , e scriviamo se almeno una proiezione combacia, ovvero se Più grande è , minori saranno i falsi negativi.
La probabilità che e non siano simili è data dalla probabilità che tutte le proiezioni non combacino Dato che le proiezioni sono indipendenti tra loro, è possibile scomporre la congiunzione degli eventi nel prodotto delle loro probabilità e, dato che la probabilità che esse non coincidano è la stessa qualunque sia la proiezione, possiamo scrivere: Infine scriviamo che è simile a con probabilità Se sull'asse delle indichiamo la similarità, la funzione ha il seguente andamento ad (per ed ):
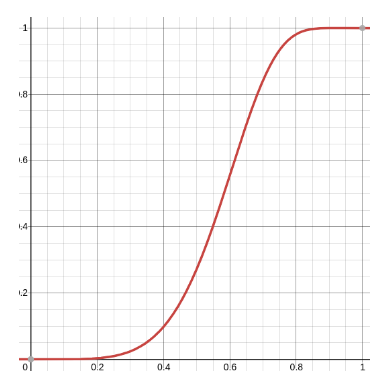
Esempio
Supponiamo che ed e siano i due vettori Quindi procediamo a generare gli insiemi casuali:
- per abbiamo e , nessun match quindi proseguiamo;
- per abbiamo e , nessun match quindi proseguiamo;
- per abbiamo e , match! I vettori e sono simili.
5.4.3 LSH e min-hashing
Sia la matrice delle signatures di dimensione (m funzioni hash ed documenti) . Dividiamo le righe in bande (o gruppi contingui) ognuna formata da righe. Sia la soglia di similarità, allora utilizzando il LSH avremo la seguente situazione:
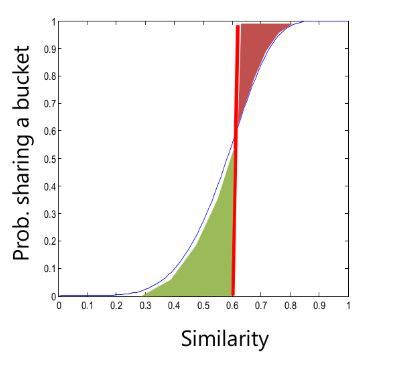
Se la linea rossa coincide con la soglia di similarità, l'area verde che la precede è la probabilità di incappare in un falso positivo, mentre l'area rossa che la succede è la probabilità di incappare in un falso negativo. Idealmente, vorremmo una funzione step che rifiuti tutto prima della soglia , dopodiché accetti tutto.
Esempio
Supponiamo che la soglia sia e che la similarità tra due insiemi di shingle ed sia Consideriamo e , quindi dividiamo la nostra matrice in 20 bande da 5 righe ciascuna. Per i teoremi precedenti, sappiamo che la probabilità che un minhash tra i due insiemi corrisponda all'interno della banda è: La probabilità che tutti i minhash corrispondano all'interno di una banda (ricordando ) è . Se consideriamo l'insieme degli hash in tutte le bande, avremo che: Quindi è simile ad con probabilità del %. Osserviamo come si comporta la funzione con coppie dissimili, quindi supponiamo: Avremo che Quindi è simile ad con probabilità del %, ovvero è poco probabile che essi risultino simili.
Caso ideale
Idealmente vorremmo che
5.4.4 Algoritmo LSH offline
- Per ogni feature vector , si calcola .
- Per ogni si crea un clustering (insieme di cluster differente per ogni banda) tale che due feature vector e si trovino nello stesso cluster se .
- Si crea un grafo non direzionato in cui i nodi e sono connessi se esiste un cluster che li contiene entrambi.
- Si calcolano le componenti connesse del grafo per identificare vettori simili.
Offline algorithm from Mining of massive datasets
If we have minhash signatures for the items, an effective way to choose the hashings is to divide the signature matrix into b bands consisting of r rows each. For each band, there is a hash function that takes vectors of r integers (the portion of one column within that band) and hashes them to some large number of buckets. We can use the same hash function for all the bands, but we use a separate bucket array for each band, so columns with the same vector in different bands will not hash to the same bucket.
5.4 Famiglie di funzioni LSH
L'esempio visto precedentemente è un esempio di famiglia di funzioni LSH, che possono essere combinate per distinguere coppie di punti distanti tra loro da coppie di punti vicini tra loro.
Una funzione locality sensitive è una funzione che soddisfa le seguenti 3 condizioni:
- Le coppie vicine devono essere candidate con probabilità maggiore rispetto alle coppie lontane.
- Deve assicurare l'indipendenza statistica per ogni operazione svolta.
- Deve essere efficiente:
- Il tempo necessario ad identificare le coppie candidate deve essere molto minore rispetto al tempo necessario per calcolare la distanza tra tutte le coppie.
- Si deve poter combinare per costruire delle funzioni più potenti che permettano di evitare falsi positivi e falsi negativi.
Una funzione locality sensitive prende in input 2 oggetti e decide se essi sono simili o meno, o perlomeno candidati ad essere simili (per poi computare la distanza successivamente su un insieme ristretto di oggetti) Una collezione di funzioni locality sensitive prende il nome di famiglia di funzioni locality sensitive. Diciamo che una famiglia è -sensitive se :
- Se la distanza allora la probabilità che è almeno
- Se la distanza allora la probabilità che è al più
5.4.1 Amplificare una famiglia locality sensitive
Costruzione in AND
Si costruisca una nuova famiglia dove ogni funzione è costruita da un insieme di cardinalità di funzioni della famiglia . Asseriamo che è costruita da tale che Questo processo è chiamato costruzione in AND e garantisce la costruzione di una famiglia -sensitive. In questo modo andiamo a ridurre entrambe le probabilità e, di conseguenza, il numero di falsi positivi.
Costruzione in OR
Si costruisca una nuova famiglia dove ogni funzione è costruita da un insieme di cardinalità di funzioni della famiglia . Asseriamo che è costruita da tale che Questo processo è chiamato costruzione in OR e garantisce la costruzione di una famiglia -sensitive. In questo modo andiamo ad aumentare entrambe le probabilità e, di conseguenza, riduciamo il numero di falsi negativi.
Le costruzioni in OR e in AND possono essere combinate in cascata per spingere la probabilità bassa a 0 e la probabilità alta a 1.
Esempio
Partiamo da una famiglia -sensitive ed eseguiamo una prima costruzione: Applicando in cascata prima una costruzione in AND con e dopodiché una costruzione in OR con . Le probabilità e della nuova famiglia saranno: Quindi sarà una famiglia -sensitive. Osserviamo che con questo approccio, la probabilità più bassa è stata schiacciata a 0.
Se costruiamo la famiglia in maniera inversa, quindi applicando in cascata prima l'OR e poi l'AND, avremo che le probabilità saranno: Quindi sarà una famiglia -sensitive. Invertendo il processo, la probabilità più alta è stata spinta verso 1.
Tentiamo adesso di costruire una famiglia applicando in cascata le seguenti costruzioni: Dove da ad applichiamo prima un AND (=4) e poi un OR () e da ad applichiamo prima un OR () e poi un AND (). Così facendo, le probabilità e saranno ricalcolate come segue: Plottando queste funzioni, avremo una curva molto più ripida che approssima meglio la step function ideale. Una soluzione del genere riduce molto bene sia il numero di falsi positivi che il numero di falsi negativi.
5.4.2 LSH su diverse distanze
Min hashing
La famiglia delle funzioni min-hash, assumendo che esse usino la distanza di Jaccard, sono Per ogni e tale che . Per le altre distanze non vi è alcuna garanzia che vi siano funzioni hash locality sensitive. Vedremo alcune delle più famose di seguito.
Distanza di Hamming
Siano e due vettori binari di dimensione , denotiamo con la loro distanza di Hamming. Definiamo una funzione che rappresenti l'-esimo elemento del vettore . Possiamo affermare che se e solo se e combaciano nell'elemento -esimo. La probabilità che combacino è Possiamo definire la famiglia di funzioni locality sensitive come una famiglia Con .
Distanza del coseno
La distanza del coseno ha senso in spazi aventi delle dimensioni (come gli spazi Euclidei o le versioni discrete degli spazi Euclidei). In tali spazi i punti hanno delle direzioni. La distanza del coseno tra due punti corrisponde all'angolo tra questi; tale angolo sarà definito tra 0° e 180° a prescindere da quante dimensioni sia costituito lo spazio. Possiamo calcolare la distanza del coseno calcolando prima il coseno dal rapporto tra il prodotto scalare tra i due vettori ed il prodotto tra le loro norme, poi applicando l'arcocoseno: È possibile dimostrare che la distanza del coseno è una misura di distanza. Se volessimo normalizzare il valore della distanza tra 0 ed 1, basterebbe dividere per Supponiamo di considerare due vettori ed . Tali vettori potrebbero trovarsi in uno spazio con molte dimensioni, Tuttavia insieme definiscono un piano e l'angolo tra loro e misurato sul tale piano:
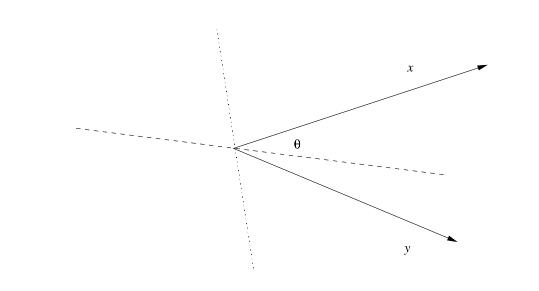
Selezionando in maniera casuale un iperpiano che passa dall'origine (asse tratteggiato in figura), esso intersecherà il piano formato da e . Per selezionare un iperpiano in maniera casuale, selezioniamo casualmente un vettore (asse punteggiato in figura), che sarà il suo vettore normale, dopodiché tutti i punti ortogonali a saranno punti appartenenti all'iperpiano.
Se effettuiamo il prodotto scalare tra ed i due vettori in figura, avremo prodotti con segni differenti: questo poiché essi capitano in lati opposti dell'iperpiano. Se l'iperpiano fosse stato l'asse punteggiato ed il suo vettore normale l'asse tratteggiato, allora i prodotti scalari avrebbero avuto lo stesso segno poiché dalla stessa parte dell'iperpiano.
In sintesi, preso un vettore random, definiamo la funzione hash Se il segno è positivo, i due vettori formeranno un angolo minore di , viceversa se il segno è negativo. La famiglia di funzioni locality sensitive per la distanza del coseno è formata da funzioni tale che: Si dimostra che la famiglia di funzioni appena definità è una famiglia
Al paragrafo 3.7.3 di Mining of massive datasets vi è un semplice trucco per la generazione degli sketch per vettori a cui deve essere applicata la distanza del coseno. Tale trucco consiste nel generare vettori casuali le cui componenti sono esclusivamente formate da +1 e -1, così che il prodotto scalare diventi la somma degli elementi a cui corrisponde un +1, a cui viene sottratta la somma degli elementi a cui corrisponde un -1.
Inoltre vi è un esempio che spiega come viene stimata la distanza del coseno. Supponiamo che gli sketch tra due vettori siano e , essendo che solo degl elementi combaciano, si stima come distanza un angolo di 120°.
Distanza Euclidea
Per semplicità, supponiamo di trovarci in uno spazio bidimensionale. Ogni funzione hash della famiglia è associata ad una retta casuale nello spazio. Fissata una costante dividiamo la retta in segmenti di lunghezza .
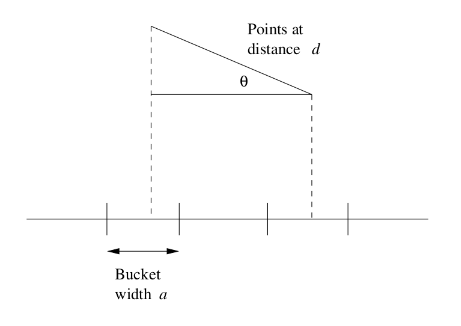
I segmenti sulla linea corrispondono ai b nerico punto è collocato nel bucket (segmento) in cui propria proiezione rispetto alla retta va a finire. Se la distanza tra due punti è molto più piccola rispetto alla costante , allora c'è una buona chance che i due punti vengano hashati nello stesso bucket, in tal caso, la funzione dichiara che i punti sono uguali.
a) Se , allora vi è almeno il 50% () di possibilità che essi ricadano nello stesso bucket. Se l'angolo formato dai due punti rispetto alla retta è grande, allora la probabilità che i punti ricadano nello stesso bucket è ancora maggiore: se rispetto ad , allora i due punti ricadranno per certo nello stesso bucket (la retta che passa tra i due punti è perpendicolare alla retta ).
b) Supponiamo che , quindi che i punti siano distanti tra loro: per cadere all'interno dello stesso bucket è necessario che . Basti guardare la figura, proiettando la distanza sulla retta essa è più grande di , quindi i punti staranno per certo in bucket differenti. Se allora la possibilità che i due punti ricadano nello stesso bucket è inferiore ad : infatti affinché il coseno sia inferiore ad (in modo da far rientrare le proiezioni nello stesso bucket) l'angolo deve stare tra 60° e 90°, ma l'angolo può assumere con probabilità uniforme un valore compreso tra 0° e 90°, quindi la probabilità che assuma quel range di valori è effettivamente .
La famiglia appena mostrata è una famiglia -sensitive. Il problema legato a tale famiglia sono le probabilità che non variano al variare del coefficiente . Tuttavia, è possibile effettuare delle costruzioni in AND ed in OR per manipolare tali probabilità.
6. Link analysis
Il web è un grafo orientato i cui nodi sono rappresentati dalle pagine web, mentre gli archi corrispondono ai link tra le pagine. Data una query di ricerca, il problema del web search consiste nel restituire dei siti web coerenti con la query, ma soprattutto autorevoli. Il primo approccio alla navigazione web fu' la web directory, ovvero un elenco di siti web curati manualmente e suddivisi in maniera gerarchica. Una web directory non è un motore di ricerca e risulta essere molto limitante. Il secondo tentativo fu' proprio il web search, che consiste in due problemi: il primo problema è il più semplice, consiste nel trovare un insieme di pagine che contengono parole in comune con la query, il secondo problema è più complesso e consiste nel ritornare solo pagine web autorevoli ed evitare lo spam.
6.1 PageRank
Il PageRank è un algoritmo di link analysis creato da Page, uno dei due fondatori di Google. Supponiamo di dare un valore di importanza iniziale a tutti i nodi, interpretiamo i link come dei "voti" e, se un nodo ha 10 link uscenti, allora dividerà la propria importanza equamente tra tutti e 10 i nodi. I link da pagine web importanti contano di più e tale concetto è implementabile attraverso la ricorsione.
6.1.1 Formulazione ricorsiva di base
Ogni voto di un link è proporzionale all'importanza della sua pagina sorgente. Se la pagina con importanza ha link uscenti, ogni link prende voti. L'importanza di è la somma dei voti dei suoi link entranti. Possiamo osservare che un voto da una pagina importante vale di più, e che una pagina è importante se viene puntata da altre pagine importanti. Definiamo il rank per la pagina attraverso una equazione di flusso Quindi il rank è dato dalla somma, per tutti i nodi che puntano a , del voto del nodo , che è calcolato dividendo la sua importanza per il suo grado uscente. Vediamo un grafo d'esempio
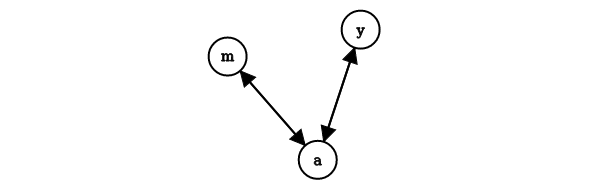
In questo caso avremo che Questo è un sistema di 3 equazioni in 3 incognite con infinite soluzioni (equivalenti a meno di un fattore di scala). Un vincolo addizionale rende la soluzione unica: Da cui otteniamo che , ed . Con un risolutore di equazioni lineari è possibile trovare le soluzioni per piccoli grafi. Tuttavia, il grafo del web è massivo e necessita di una nuova formulazione.
6.1.2 Formulazione matriciale
Supponiamo di avere una matrice di adiacenza per il grafo del web e consideriamo la formulazione stocastica di tale matrice, ovvero: La riga -esima della matrice indica gli archi entranti ad . L'elemento vale se il nodo , supponendo abbia archi uscenti, ha un arco uscente che punta ad . Strutturando così la matrice avremo che la somma delle colonne sarà pari ad 1.
6.1.3 Vettore dei rank
Introduciamo un vettore , chiamato vettore dei rank, tale che per ogni componente , indichi il rank del nodo -esimo. Imponiamo come vincolo che la somma delle componenti sia 1, quindi . Possiamo riscrivere l'equazione di flusso (1) nel seguente modo: Nel prodotto riga colonna, la componente di verrà calcolata attraverso la somma dei rank dei nodi che puntano a (informazione contenuta nel vettore ), diviso per il loro grado uscente (informazione contenuta nella matrice ). Osserviamo che è un autovettore della matrice stocastica , con corrispondente autovalore . Possiamo dire inoltre che 1 è l'autovalore più grande, essendo una matrice stocastica sulle colonne (con entry non-negative). A questo punto è possibile ottenere attraverso il metodo Power iteration:
- Supponiamo di avere pagine web, inizializziamo ;
- Iteriamo lo step di aggiornamento
- Fermiamo l'iterazione quando
Calcoliamo il rank vector per l'esempio precedente (2). La matrice stocastica sarà Inizializziamo casualmente Quindi computiamo E continuiamo fino a convergenza.
6.1.4 Random walk surfer
Immaginiamo un random web surfer, ovvero qualcuno che navighi tra le pagine del web attraverso i link. Se al tempo il surfer è sulla pagina , allora al tempo il surfer seguirà uno tra i link uscenti di in maniera casuale ed uniforme. Il processo è ripetuto all'infinito.
Sia il vettore la cui -esima componente indica la probabilità che il surfer sia alla pagina a tempo . Allora è la distribuzione di probabilità sulle pagine del web. Possiamo descrivere il cammino del random surfer come un processo markoviano, per cui avremo Supponiamo che si raggiunga uno stato per cui Allora sarà la distribuzione stazionaria del random walk. Il nostro vettore soddisfa , quindi è la distribuzione stazionaria della random walk eseguita dal random web surfer. Dallo studio delle catene di Markov si evince che per grafi che soddisfano certe condizioni, la distribuzione stazionaria è unica e sarà raggiunta a prescindere da quali saranno le probabilità iniziali a tempo .
6.1.5 Oscillazioni, dead-end e spider-trap
In alcuni casi la computazione del page rank potrebbe non convergere. Vediamo un primo caso in cui si presenta un ciclo nella rete ed il risultato oscilla all'infinito:

Supponiamo di inizializzare , allora avremo ovvero una soluzione che oscilla all'infinito e non converge mai. Osserviamo un altro caso:

Il nodo è un dead-end, ovvero un nodo che non ha link uscenti. Se il random walk si trova sul nodo , allora vi rimane per sempre. I nodi dead-end causano la perdita dell'importanza, fenomeno denominato leak out. Osserviamo un ultimo caso:
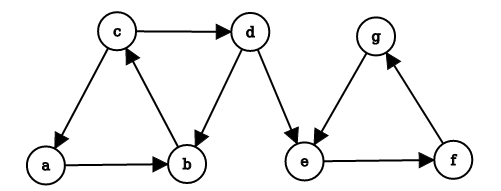
Quando il random walker entrerà nel nodo , navigherà per sempre all'interno del gruppo e non uscirà mai. Questa situazione è chiamata spider-trap, poiché il random walker è intrappolato all'interno del gruppo di nodi. La spider-trap assorbirà tutta l'importanza (esempio p.174, Mining of massive datasets).
6.1.6 Teleport
La soluzione di Google ai problemi elencati precedentemente prende il nome di teleport. Ad ogni step, il random surfer ha due opzioni:
- Con probabilità segue un link in modo random
- Con probabilità salta ad un nodo random
Valori comuni per sono nel range . Il surfer sarà teletrasportato fuori dalla spider-trap in un numero ragionevole di time-step. Questo approccio non solo risolve i problemi, ma riflette la realtà dei fatti: un navigatore del web può utilizzare la barra dell'URL per direzionarsi ad un'altra pagina anziché continuare a seguire i link. A questo punto illustriamo l'equazione di flusso del PageRank [Brin-Page, '98] In questa formulazione non ha dead-end. È possibile pre-processare la matrice e rimuovere tutti i dead-end, oppure eseguire il teleport con probabilità 1 per uscire dal dead-end. Possiamo introdurre la matrice di Google formulata attraverso la precedente equazione, come: Ancora una volta è possibile applicare la power iteration per trovare il vettore dei rank , infatti
6.1.7 Ottenere l'equazione
Aggiungere il teleport al PageRank equivale a tassare ogni pagina di una frazione del suo score e ridistribuirlo uniformemente tra i nodi. Partendo dall'equazione E sapendo che è definita come nella equazione (12), possiamo scrivere che: Ma ricordando il vincolo possiamo scrivere Che equivale a scrivere
6.1.8 Algoritmo completo
Presi in input
- Il grafo diretto (con spider-trap e dead-end)
- Il parametro
L'algoritmo consiste nei seguenti passi:
- Si inizializza
- Sinché si ripete:
- Per ogni :
- se
- se
- Per ogni :
- dove
- Si assegna
- Per ogni :
- Si ritorna in output
Si noti che nell'algoritmo non si aggiunge ad direttamente un valore , ma si passa per una variabile intermedia . Ciò è fatto per evitare di normalizzare il vettore alla fine di ogni iterazione (per rispettare il vincolo tale che la somma delle componenti sia 1). Una volta aggiornato si sommano in tutte le sue componenti e si ottiene un valore . Vogliamo che la somma delle componenti sia 1, quindi distribuiamo il residuo uniformemente alle componenti. Il passo è analogo ad aggiornare il vettore con la regola del PageRank e normalizzare alla fine.
6.2 Ingegnerizzazioni del PageRank
Il passo chiave del PageRank è la moltiplicazione tra la matrice ed il vettore . L'algoritmo è semplice se si ha memoria principale a sufficienza. Supponiamo che il numero di pagine sia miliardo e che ogni entry occupi byte. I vettori ed occupano circa GB (2 miliardi di entries). La matrice ha entries, ovvero , che è un numero davvero grande.
6.2.1 Matrice di adiacenza sparsa
La matrice di adiacenza del grafo del web è molto sparsa, risulta quindi insensato scegliere (nella pratica) una rappresentazione come quella matriciale. È possibile codificare la matrice utilizzando solo le entry diverse da 0, con uno spazio occupato proporzionale al numero di link (es. con le liste di adiacenza).
6.2.1 Operazioni in memoria secondaria
Supponiamo che solo stia in memoria, mentre la matrice e siano conservati sul disco. Possiamo modificare l'algoritmo PageRank ed operare nel seguente modo:
- Inizializziamo tutte le entry di a
- Per ogni nodo :
- Si legge sul disco ( = outlink)
- Per ogni si aggiorna :
Ad ogni iterazione bisogna leggere ed dal disco e scrivere su disco, quindi il costo per iterazione del power method è .
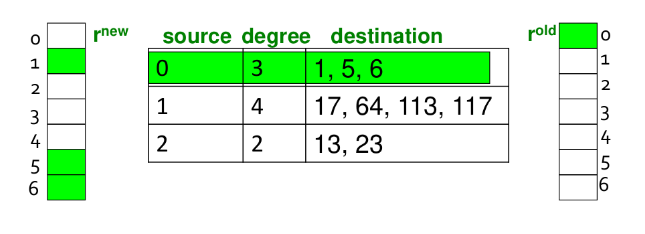
6.2.2 Aggiornamento block-based
Se lo spazio in memoria principale non fosse sufficiente ad ospiare , si potrebbe pensare di suddividere il vettore in blocchi che entrano in memoria. In tal caso si scansionerebbero ed una volta per ogni blocco, con un costo per iterazione di power method pari a .
Tuttavia possiamo ottimizzare l'algoritmo escludendo del lavoro inutile: ipotizziamo di avere in memoria il blocco di di indici . Iniziando per , andiamo a recuperare la lista di adiacenza e controlliamo i suoi outlink. Supponiamo che gli outlink di 0 siano , allora anziché aggiornare tutti gli outlink di 0, si aggiornano solo quelli contenuti nel blocco, in questo caso .
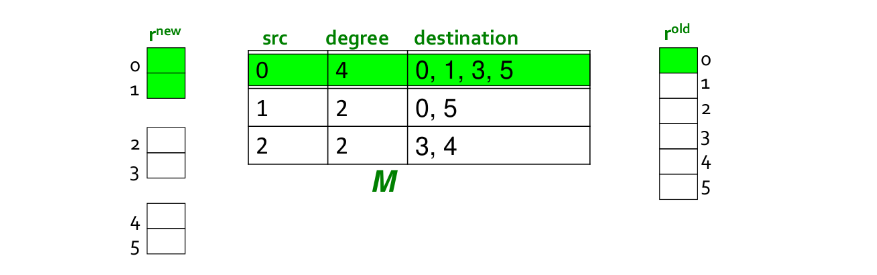
6.2.3 Block-Stripe Update Algorithm
Nel paragrafo precedente abbiamo un algoritmo che, per ogni iterazione, legge la matrice (che è molto più grande di ) volte. Per evitare questa lettura continua è possibile suddividere in striscie: ogni striscia conterrà solo i nodi destinazione del corrispondente blocco in . Avremo un overhead per striscia trascurabile ed un costo per iterazione di power metodo di ( indica l'overhead).
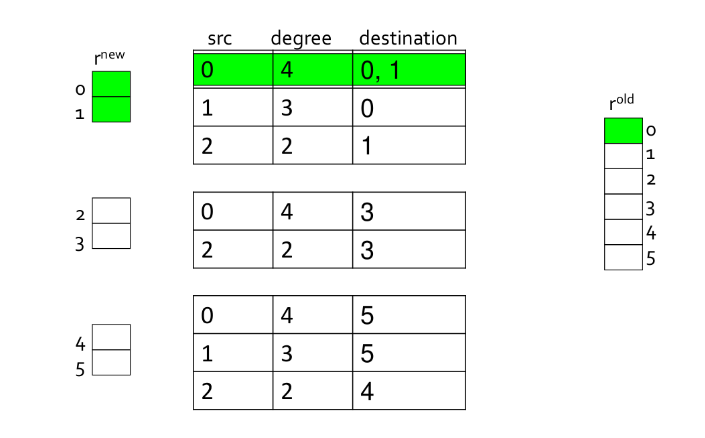
6.3 Topic-Specific PageRank
Supponiamo di immetere la query "trojan" su un motore di ricerca: la ricerca potrebbe essere legata alla sicurezza informatica, alla storia (cavallo di Troia) etc... per cui è necessario un processo di disambiguazione. L'idea del topic-specific PageRank consiste nell'aggiungere un bias alla random walk: quando il walker si teletrasporta, sceglie una pagina da un insieme , chiamato insieme di teletrasporto (teleport set). contiene solo pagine che sono rilevanti per il particolare topic (ottenibile da strutture come le Open Directory). Per ogni teleport set , otteniamo un vettore specifico che ci indica l'importanza delle pagina per il particolare topic.
6.3.1 Formulazione matriciale
Per far si che questo funzioni è necessario aggiornare il teletrasporto nella formulazione del PageRank e definire la matrice per casi: La matrice è ancora stocastica. Vengono pesate allo stesso modo tutte le pagine all'interno del teleport set . È possibile anche assegnare pesi differenti alle pagine con soluzioni più sofisticate.
Essendovi un teleport set per ogni topic, avremo più vettori di rank calcolati considerando di volta in volta un teleport set differente. Così facendo si ottengono dei vettori di importanza delle pagine differenti per ogni topic.
6.4 SimRank
L'algoritmo SimRank serve a misurare la similarità (o prossimità) dei nodi di un grafo. Supponiamo di trovarci in un grafo -partito con tipi di nodi. Supponiamo di voler misurare il SimRank score per un nodo , l'idea dietro l'algoritmo consiste in una random walk partendo da con un teleport set contenente solo il nodo analizzato. Questo particolare tipo di random walk prende il nome di random walk with restart, poiché il teleport riporta sempre al punto di partenza.
6.4.1 Esempio
Consideriamo un grafo tripartito con tre tipi di nodi: Autori, Conferenze e Tag. Ogni autore è collegato a diverse conferenze ed ogni conferenza è collegata a diversi Tag. Siamo interessati a calcolare la similarità tra gli autori del grafo. Si procede calcolando il SimRank per ogni autore, tale score conterrà dei valori interpretabili come la similarità con tutti i nodi del grafo.
6.5 Web spam
Si considera spamming qualsiasi azione deliberata per far avanzare una pagina web nelle posizioni dei risultati di un search engine, con un valore molto più alto di quello reale. Nel caso di studio, lo spam equivale ad una pagina web emersa come risultato dello spamming. Una più ampia definizione si trova nel contesto della Search Engine Optimization (SEO).
I primi Search Engine non riuscivano a bloccare lo spam poiché si basavano esclusivamente sul contenuto testuale delle pagine in relazione alla query di ricerca. Supponiamo che lo spammer abbia un negozio di magliette e che la parola "tennis" sia il trend del momento. Allora basterà aggiungere alla propria pagina e-commerce tante volte la parola "tennis" e nascondere il testo in qualche modo. Se un utente avesse cercato "tennis", lo shop di magliette sarebbe stato ben posizionato nei risultati del motore di ricerca. Google fornì una soluzione al problema basandosi su un concetto semplice: "Credere in quello che dicono le persone di te e non a quello che dici tu di te stesso". Quindi se le pagine che puntavano con dei link allo shop di magliette non parlavano di tennis, allora molto probabilmente lo shop di magliette non parla di tennis, quindi viene penalizzato nella ricerca.
6.5.1 Spam farm
Quando Google divenne il motore di ricerca dominante, gli spammer si misero alla prova cercando di eludere il sistema: vennero fuori le spam farm. Categorizziamo le pagine in base alla accessibilità dello spammer:
- Le pagine inaccessibili sono pagine a cui lo spammer non ha accesso
- Le pagine accessibili sono pagine in cui lo spammer può inserire contenuto limitatamente
- Le pagine possedute dallo spammer sono le pagine che si vuole far emergere
La spam farm consiste nell'andare a creare il maggior numero di link che vanno da pagine accessibili alle pagine possedute, di cui si vuole migliorare il ranking. Esempi di pagine accessibili sono i blog o i social network, dove è possibile inserire del contenuto.
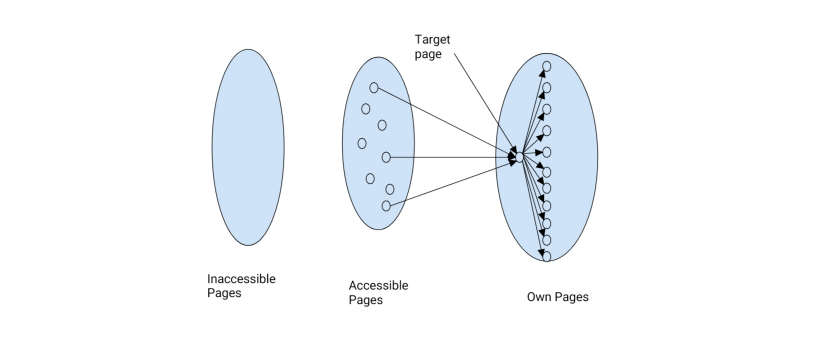
6.5.2 Spam gain
Supponiamo di voler calcolare lo score del PageRank di una pagina su cui agisce una spam farm. Sia il contributo (incognito) di PageRank dato a dalle pagine accessibili. Supponiamo che sia collegato ad pagine possedute e ogni pagina posseduta sia collegata solamente a . Sia il PageRank di , allora possiamo dire che cede ad ognuna delle M pagine accessibili uno score pari a
Dato che le pagine possedute sono collegate solo a , restituiranno questo score, tuttavia ridotto a a causa del contributo del teletrasporto. Quindi sommando questi contributi ad e considerando il teletrasporto, abbiamo che è definito come segue
Se risolviamo l'equazione per
È possibile omettere dall'equazione il termine poiché prossimo a 0, quindi riscriviamo
Essendo al numeratore, aumentando il numero di pagine possedute è possibile aumentare il rank della pagina .
Google Bombing
Un'altro modo di ingannare un search engine è il bombing. Consiste nel far puntare le pagine proprie e quelle accessibili, che trattino di uno specifico topic , verso una pagina web non accessibile, aumentando il punteggio di quest'ultima nei confronti del topic . Un tipico esempio è il bombing al presidente Bush, associato a topic denigratori.
6.6 TrustRank
Un approccio naive per combattere il link spam consiste nell'inserire in una blacklist tutte le strutture che sembrino simili a delle spam farm. Tuttavia, è stato sviluppato un algoritmo che permette di calcolare un punteggio legato alla affidabilità della fonte, chiamato TrustRank: consiste in un topic-specific PageRank, con un teleport set di pagine trusted (affidabili), come i siti governativi (.gov), i siti educazionali (.edu), etc.
6.6.1 Implementazione del TrustRank
Il principio di base è quello di approssimare l'isolamento: è raro che una pagina "buona" punti ad una pagina "cattiva" (spam). Si parte da un insieme di pagine web, chiamato seed set, curato manualmente. Risulta particolarmente dispendioso creare un seed set, per cui è un insieme molto ridotto.
L'insieme di teletrasporto corrisponde al seed set. Si inizializza ad 1 il valore di trust di ogni pagina all'interno di , mentre si inizializza a 0 la trust delle pagine esterne ad . Il TrustRank propaga la trust dalle pagine in alle pagine esterne, come succede nel PageRank. Sia l'insieme di out-link della pagina , allora per ogni pagina , riceverà da un contributo di trust pari a Dove ci ricorda che una parte di trust è riservata al meccansismo di teleport a delle pagine trusted. La trust è additiva, quindi la trust della pagina è la somma di tutte le trust conferite a delle pagine che la linkano. Entro un fattore di scala, il TrustRank corrisponde al PageRank, con le pagine trust come teleport set. Alcune osservazioni:
- Attenuazione della trust: la trust decresce con la distanza nel grafo
- Trust splitting: più sono gli outlink, minore sarà il contributo di trust trasferito.
6.6.2 Costruzione del Seed Set
Il seed set è manualmente curato e deve essere più piccolo possibile. Allo stesso tempo esso deve assicurare che ogni pagina buona ottenga un trust rank sopra la soglia: le pagine buone devono essere raggiungibili dal seed seed con un cammino relativamente corto. Da queste osservazioni in contrasto possiamo comprendere quanto sia complesso prelevare un buon seed set. Le due principali tecniche sono:
- Eseguire un PageRank e selezionare le pagine con rank più alto (difficilmente di spam);
- Utilizzare delle pagine la cui appartenenza è controllata (.edu, .gov, .mil)
6.7 HITS: Hub and Authorities
HITS (Hyperlink-Induced Topic Search) è un algoritmo, sviluppato da Jon Kleinberg, di valutazione delle pagine web in funzione dei link. Pubblicato nello stesso periodo del PageRank, ha avuto meno successo ma introduce comunque un'idea interessante. Supponiamo di voler trovare un buon quotidiano: anziché trovare i quotidiani migliori da soli, ci rivolgiamo ad un esperto che sappia consigliarci, linkando in modo coordinato a buoni quotidiani. Ancora una volta si presenta il concetto di link come voti. Definiamo due score:
- Qualità di esperto (hub): voti totali ricevuti dalle authority che puntano a loro
- Qualità sui contenuti (authority): voti totali ricevuti dagli esperti
Ogni pagina avrà entrambi gli score, ed in base a questi (le pagine interessanti) si divideranno in due classi:
- Le Authority sono pagine che contengono informazioni utili (Home di un quotidiano)
- Gli Hub sono pagine che si collegano alle authority (Elenchi di quotidiani)
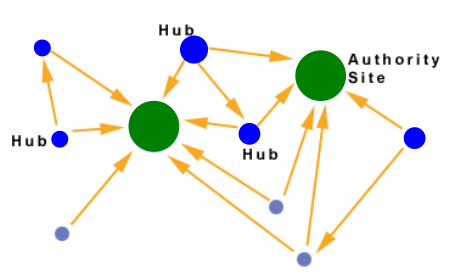
L'intuizione è che un buon hub linka diverse buone authority, ed una buona authority è linkata da diversi buoni hub. Vediamo una approssimazione intuitiva della procedura:
- Si inizializza lo score di hub ad 1 per ogni nodo
- Si calcola l'autority di ogni nodo sommando l'hub di ogni suo link entrante
- Si calcola l'hub di ogni nodo sommando l'authority di ogni suo link uscente
- Si riparte dal secondo step sino ad una stabilizzazione (con dovuti accorgimenti)
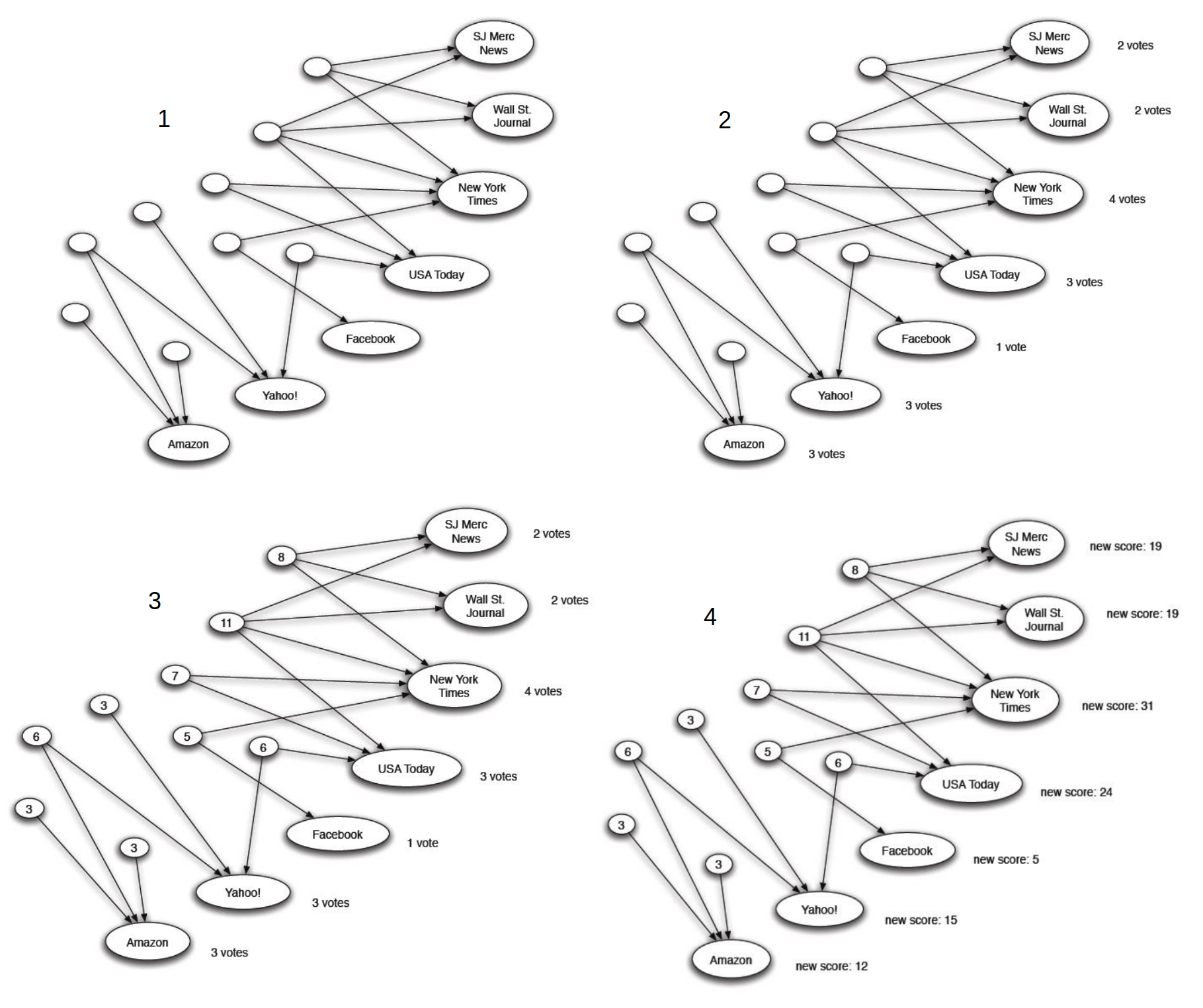
6.7.1 Algoritmo
Ogni pagina ha un authority score ed un hub score . Al tempo 0 si inizializzano gli score per ogni nodo all'interno del grafo:
Dove è il numero di nodi. Si itera la seguente procedura sino alla convergenza:
- Per ogni nodo al tempo si calcola l'autority:
- Per ogni nodo al tempo si calcola l'hub:
- Si normalizzano i risultati imponendo
L'algoritmo converge ad un singolo punto stabile.
6.7.2 Algoritmo in notazione vettoriale
Indichiamo con il vettore di tutti gli autorithy score, e con il vettore di tutti gli hub score. Sia la matrice di adiacenza (ricordando che se , 0 altrimenti), allora possiamo scrivere che Ne segue che . In modo simile possiamo scrivere che Ne segue che . Quindi riscriviamo l'algoritmo in notazione vettoriale, inizializzando:
E iterando sino a convergenza
- Si normalizzano ed
I criteri di convergenza, considerando un valore piccolo, sono:
Possiamo incorporare la normalizzazione nei passi di aggiornamento andando a definire
E modificando gli step di aggiornamento come segue:
È possibile effettuare delle sostituzioni:
Sotto una assunzione ragionevole di , l'algoritmo HITS converge a dei vettori e tali che
- è l'autovettore principale di
- è l'autovettore principale di
- (supp.) è l'autovalore
7. Comunità nelle reti
Le comunità sono una proprietà di tante reti reali: una comunità all'interno di una rete contiene dei nodi densamente connessi. I link tra nodi in comunità differenti sono poco frequenti.
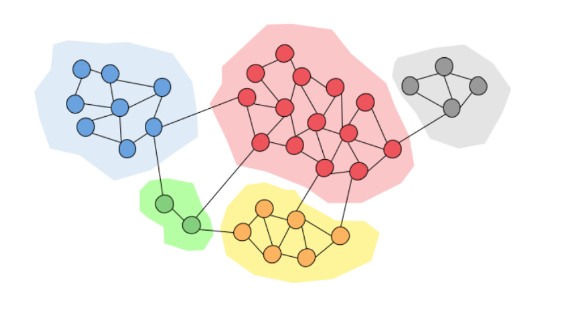
7.1 Introduzione
Possiamo pensare ai collegamenti tra nodi come un concetto di amicizia. Granovetter (1973) individuò due diverse prospettive di di amicizia:
- Amicizia strutturale: l'amicizia si distribuisce in diverse parti della rete
- Amicizia interpersonale: l'amicizia tra due persone può essere forte o debole
Un ruolo fondamentale è quello delle chiusure triadiche: se due persone in una rete hanno un amico in comune, allora c'è una più alta probabilità che questi diventino amici.
Spieghiamo il concetto di amicizia forte e debole:
- Gli archi all'interno di una struttura (es. una chiusura triadica) sono socialmente forti
- Gli archi lunghi che connettono diverse parti della rete sono socialmente deboli
Inoltre, focalizzandoci sull'informazione che naviga nella rete, possiamo dire che:
- Gli archi lunghi consentono di ottenere informazioni da parti diverse di una rete
- Gli archi all'interno di una struttura sono ridondanti in termini di accesso all'informazione
Osservazione: la perdita di una connessione forte non fa perdere informazione all'interno di una rete, al contrario, la perdita di una connessione debole causa perdita di informazione.
Osservazione: una chiusura triadica ha un alto coefficiente di clustering. Se e hanno un amico in comune, allora:
- verosimilmente incontrerà ( spende tempo con entrambi)
- e credono l'uno nell'altro poiché hanno un amico in comune
- è incentivato a legare e
Esempio: uno studio empirico di Bearman e Moody dimostra che le ragazze teenager con basso coefficiente di clustering sono più inclini al suicidio.
7.1.1 Arco ponte e ponte locale
Si definisce arco ponte un arco che, se rimosso, trasforma il grafo in un grafo disconnesso. Nell'esempio sottostante, l'arco tra e è un arco ponte.
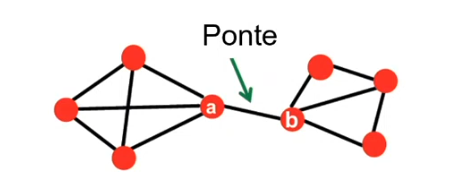
Sia un arco tra i nodi e , definiamo lo span di come la distanza tra e (endpoints dell'arco) nel caso in cui l'arco venga rimosso dal grafo. Definiamo inoltre ponte locale un arco con . Nell'esempio, l'arco tra e è un ponte locale poiché, se venisse rimosso, allora la distanza tra e sarebbe 3 ().
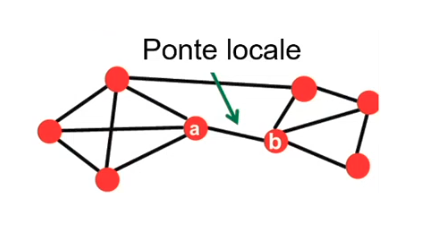
Possiamo osservare che la presenza di un ponte locale tra e ci informa implicitamente che non esiste un nodo in comune tra e . Se esistesse , allora rimosso l'arco, la distanza tra e sarebbe pari a 2 ().
Se è connesso ai nodi e , e questi ultimi sono connessi tra loro, allora parliamo di archi forti. In generale due archi forti implicano un terzo arco, ovvero esiste una chiusura triadica forte. Se non vale questa condizione, allora l'arco sarà detto debole.
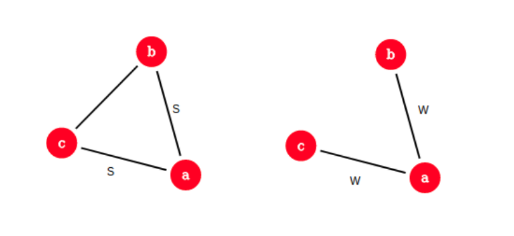
Se un nodo soddisfa una chiusura triadica forte ed è coinvolto in almeno due connessioni forti, allora un qualsiasi ponte locale adiacente ad deve essere una connessione debole.
Dimostriamolo (per assurdo): supponiamo che soddisfi una chiusura triadica forte ed abbia due connessioni forti. Sia un ponte locale ed allo stesso tempo una connessione forte. Allora deve esistere per la presenza della chiusura triadica forte. Ciò implica che non è un ponte locale (), ovvero l'assurdo.
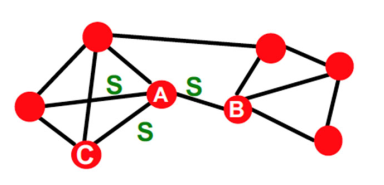
7.1.2 Neighborhood overlapping
Siano e due nodi collegati da un arco . Definiamo overlap dell'arco la quantità Dove indica l'insieme dei vicini del nodo . Quindi l'overlapping è definito come la percentuale di vicini in comune tra i due nodi collegati dall'arco.
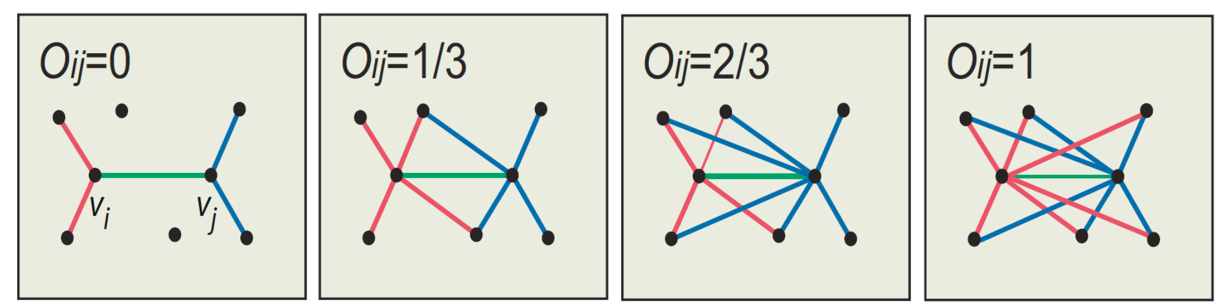
Osserviamo che quando è un ponte locale l'overlap è pari a 0, poiché non vi è nessun nodo in comune tra i due endpoint. È possibile gestire la disconnessione di un grafo basandosi sull'overlap degli archi da rimuovere: rimuovendo archi con un basso overlap, il grafo si disconnetterà prima (poiché sono connessioni poco ridondanti).
7.1.3 La teoria di Granovetter
La teoria di Granovetter suggerisce che le reti sono composte da insiemi molto connessi tra loro, chiamati comunità (cluster, gruppi, moduli). Una comunità è un insieme di nodi con tante connessioni all'interno e poche connessioni all'esterno (con il resto della rete).
7.2 Community Detection
Siamo interessati a identificare le comunità all'interno di una rete. Vedremo alcuni importanti algoritmi che lavorano sui grafi non diretti e non pesati proprio a questo scopo. Molti di questi fanno utilizzo del concetto di edge betweenness, ovvero il numero di cammini minimi che passano da un arco.
7.2.1 Algoritmo di Girvan-Newman
L'algoritmo di Girvan-Newman è un algoritmo di clustering gerarchico, basato sulla nozione di edge betweenness. L'algoritmo è pensato per archi non diretti e non pesati e consiste nell'iterare le seguenti due procedure sino a che non vi siano più archi:
- Si calcola la betweenness degli archi
- Si rimuove l'arco con più alta betweenness
L'algoritmo restituisce una decomposizione gerarchica della rete (dendogramma). Ad ogni step, le componenti connesse rappresentano le community. In seguito risponderemo alle seguenti due domande:
- Come calcolare la betweenness?
- Quante comunità vogliamo ottenere?
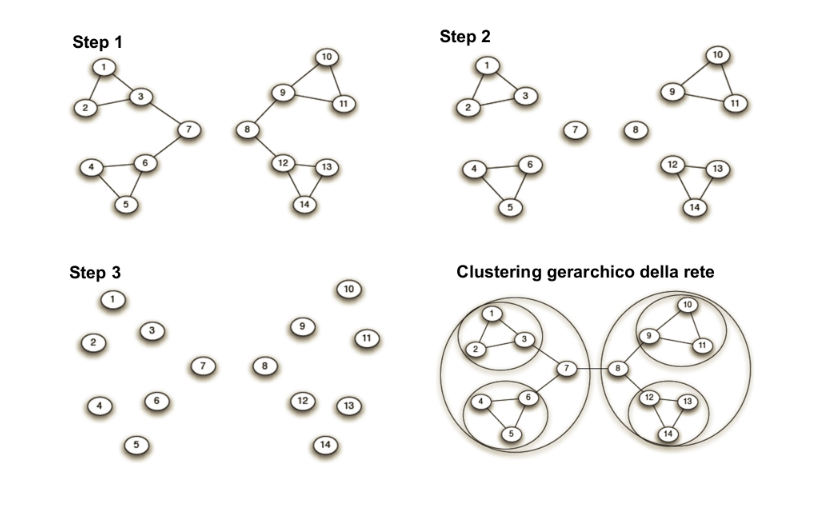
7.2.2 Calcolo della betweenness
In grafi non pesati e non direzionati, la ricerca di un cammino minimo avviene attraverso una semplice ricerca in ampiezza (BFS, breadth first search). Nel grafo di esempio è stata effettuata una ricerca in ampiezza partendo dal nodo :
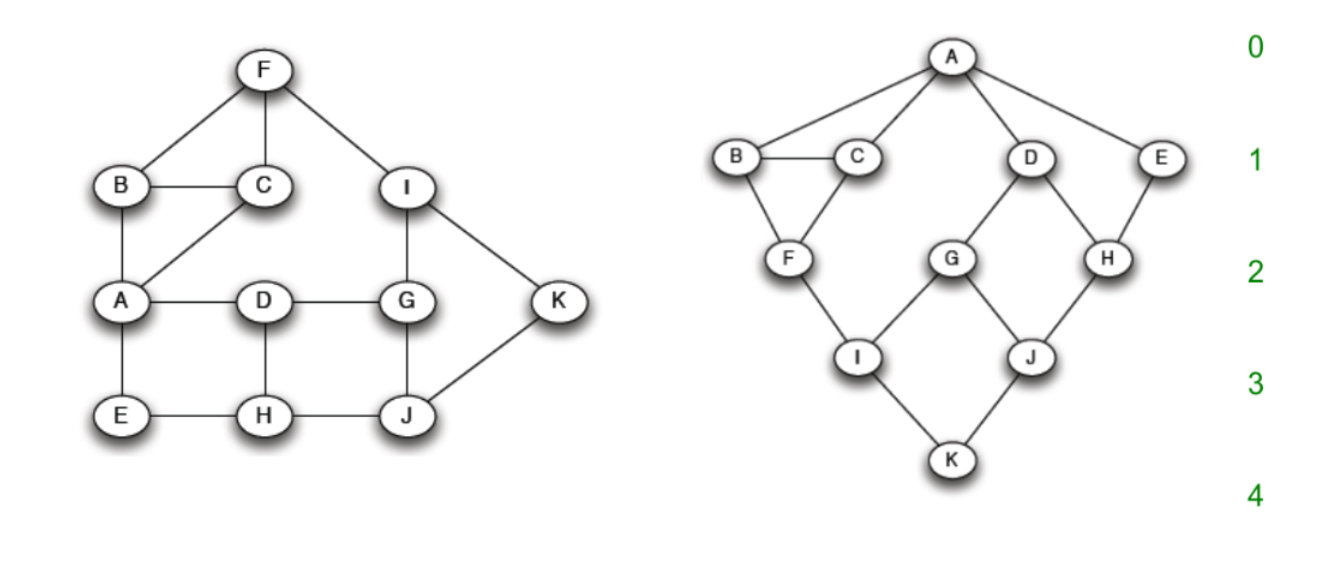
Contiamo per ogni nodo il numero di cammini minimi che vanno da ad . Tale procedura è facilmente attuabile durante la BFS. Nell'esempio, vi sono due cammini minimi che portano ad ad , uno passante per e l'altro passante per . Per cui inseriamo il valore 2 su . Calcoliamo questo valore su ogni nodo del grafo.
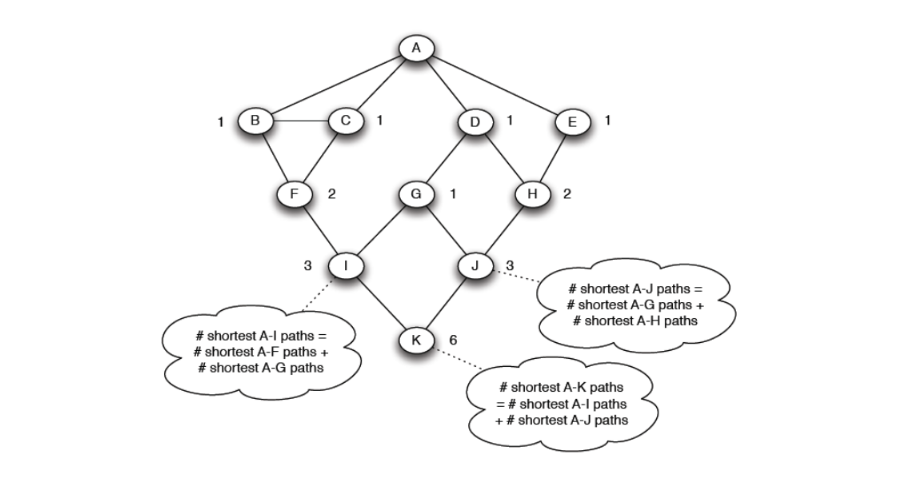
Utilizziamo questo albero per il calcolo della betweenness e illustriamo una tecnica bottom up. Supponiamo di dare un valore di flusso pari ad 1 a tutti i nodi. Partiamo dal nodo che ha 6 cammini minimi (da ). Il nodo è collegato ad che ha 3 cammini minimi, e a che ha 3 cammini minimi. Quindi i nodi hanno rispettivamente ed dei cammini minimi di . In base a questi rapporti viene diviso il flusso di ai nodi soprastanti.
Il nodo avrà a disposizione un valore di flusso pari a (1 dalla partenza, da ). ha 3 cammini minimi ed è collegato a , che ha 1 cammino minimo, e a , che ha 2 cammini minimi. Quindi i nodi hanno rispettivamente e dei cammini minimi di . Ancora una volta dividiamo il flusso in base a questi rapporti, trasferendo a e ad .
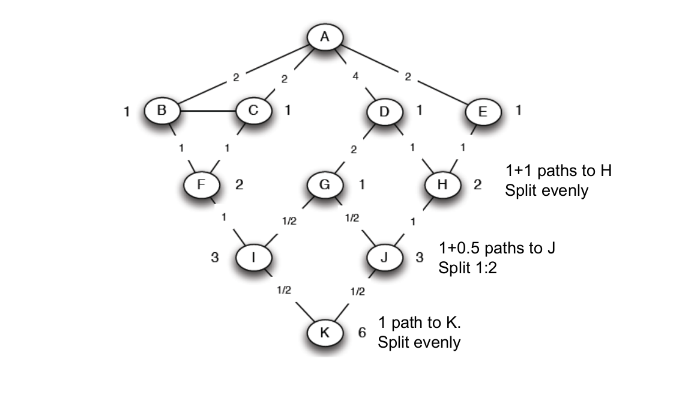
Alla fine di questa procedura, su ogni arco sarà passato un certo flusso. Questo valore viene conservato. Si ripete il processo eseguendo delle BFS su ogni nodo del grafo e per ogni BFS si sommano i valori di flusso agli archi. Alla fine dell'algoritmo si otterranno i valori di flusso per ogni nodo, che corrisponderanno alla betweenness.
7.2.3 Modularità
La modularità è una misura di come la rete è ben partizionata in comunità. Attraverso questa misura è possibile individuare il miglior partizionamento nel dendogramma risultante dall'algoritmo di Girvan-Newman, che rispetti la definizione di comunità, ovvero sottogruppi di nodi densamente connessi. Più è alta la modularità, maggiora sarà la qualità del partizionamento della rete in comunità.
Data una partizione della rete in comunità, la la modularità è tale che
Q \propto \sum_{s \in S} \Big[ \text{(#archi osservati in s}) - (\text{#archi attesi in s)} \Big]
Modello nullo
Per sapere qual è il numero atteso di archi all'interno di una comunità, è necessario prendere come riferimento un modello nullo. Un buon modello nullo è il configuration model, che mantiene la stessa distribuzione dei gradi, ma connette i nodi in modo casuale. Quindi se un nodo ha grado nel grafo reale, avrà comunque grado nel modello nullo, ma non sarà necessariamente collegato agli stessi nodi.
Data una rete reale con nodi ed archi, si costruisce una rete random . è un multigrafo: dato che i nodi si collegano in maniera casuale, allora esisterà la possibilità di collegare più volte la stessa coppia di nodi.
Se il grafo ha archi, allora possiamo individuare stubs, per immaginare cosa si intende per stub, basti tranciare la parte centrale dell'arco e dividerlo in due. Un nodo con grado avrà stub. Siano e due nodi, rispettivamente di grado e , ad una certa iterazione dell'algoritmo di costruzione del configuration model, uno stab sul nodo si collega con uno stub del nodo con probabilità Dato che ha stub, il numero atteso di archi tra e è Sommariamente, il numero atteso di archi in un multigrafo è Notando che .
Formalizzare la modularità
Una volta costruito il modello nullo, è possibile calcolare il numero atteso di archi tra due nodi. Quindi scriviamo che: Dove è la matrice di adiacenza ed il fattore normalizza la modularità tra . Empiricamente si osserva che una modularità compresa nell'intervallo indica una significativa community structure.
7.2.4 Ottimizzare la modularità
Il calcolo della betweenness è molto dispendioso, si potrebbe pensare utilizzare un algoritmo di ottimizzazione ed ottimizzare direttamente la modularità. Si dimostra che l'ottimizzazione della modularità è un problema NP-hard.
Consideriamo un sottoproblema nell'individuazione delle comunità: supponiamo di dividere la rete in due sole comunità, etichettate con -1 ed 1, e voler trovare il partizionamento che massimizzi la modularità. Definiamo un vettore detto vettore di appartenenza tale che: Riscriviamo la formula della modularità come segue: In tale formula abbiamo rimosso la prima sommatoria ed aggiunto il termine . La formula ha la stessa valenza poiché, essendovi solo due comunità, quando si analizzeranno due nodi di comunità differenti il termine , quindi il loro contributo non sarà sommato nel calcolo.
Possiamo semplificare l'espressione come segue: Dove il +1 all'interno di genera un'altra sommatoria Poiché il configuration model ha lo stesso numero di archi della rete presa in considerazione, per cui possiamo ometterlo dall'espressione (9).
Definiamo la matrice di modularità come Allora possiamo riscrivere il calcolo della modularità in forma vettoriale: Quindi Vogliamo trovare un vettore di appartenenza che massimizzi la modularità, ovvero quel partizionamento che divida il grafo in due forti comunità.
Teorema dell'autodecomposizione
Sia una matrice simmetrica e semidefinita positiva, consideriamo le autocoppie, quindi le coppie (autovalore) ed (autovettore) soluzioni dell'equazione . Si ordinino le autocoppie in maniera decrescente rispetto al proprio autovalore. Gli autovettori sono tutti ortonormali e formeranno un sistema di coordinate. Se è semidefinita positiva, tutti gli autovalori sono positivi. Dopo tali ipotesi ed osservazioni, il teorema dell'autodecomposizione asserisce che è possibile scomporre in termini dei suoi autovettori ed autovalori:
Utilizzo del teorema
La matrice è simmetrica poiché trattiamo un grafo non orientato. Riscriviamo la matrice nel calcolo della modularità in termini dei suoi autovalori ed autovettori utilizzando il teorema precedente: Quindi Se non ci sono ulteriori vincoli sul vettore , allora per massimizzare bisogna porre , ovvero l'autovettore principale. Essendo che tutti gli autovettori sono ortonormali tra loro, allora il prodotto tra e sarà nullo, per cui nella massimizzazione possiamo rimuovere la sommatoria e considerare solo l'autovettore principale: Quindi infine, anziché massimizzare direttamente la modularità, massimizziamo: Dove rimuoviamo: il quadrato, l'autovalore e il fattore normalizzante poiché non veicolano la massimizzazione della modularità.
Notiamo che se allora avrà valori diversi da . Per inserire i nodi nella giusta partizione settiamo: Dopodiché è possibile continuare la bisezione in maniera gerarchica.
7.2.5 Algoritmo veloce per l'ottimizzazione della modularità
Un algoritmo veloce per ottimizzare la modularità è il seguente:
- Si trova l'autovettore principale della matrice di modularità
- Ad esempio utilizzando il power method.
- Si dividono i nodi in base al segno degli elementi di
- Si ripete gerarchicamente sino a che
- Lo split causa un incremento della modularità e si restituisce un solo cluster
- Tutte le comunità non sono più divisibili
7.3 Spectral clustering
7.3.1 Graph partitioning
Sia un grafo non direzionato. Effettuare un bi-partizionamento (bi-partitioning task) consiste nel dividere i vertici del grafo in due gruppi disgiunti e . Come definiamo una buona partizione di ? Come possiamo trovare tale partizione in maniera efficiente?
Ma prima di tutto, cosa rende buona una partizione? Idealmente vorremmo massimizzare il numero di connessioni whitin-group (dentro il gruppo) e minimizzare il numero di connessioni between-group (tra gruppi distinti).
7.3.2 Graph cut
Partizioniamo in due gruppi e . Definiamo cut l'insieme di archi con un vertice in e l'altro in Nell'esempio sottostante si ha :
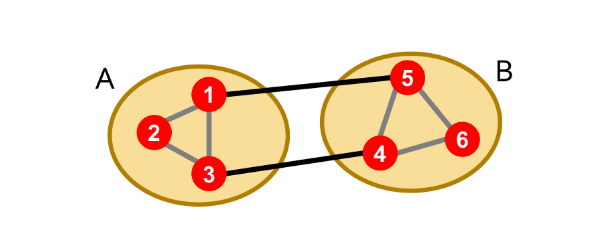
7.3.3 Minimum cut
Un criterio per ottenere un buon partizionamento del grafo è quello di minimizzare il cut, quindi scegliere come: Tuttavia abbiamo dei casi limite che tale criterio non riesce ad evitare:
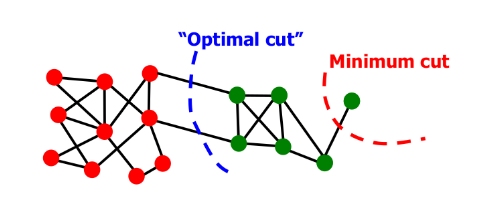
Ciò avviene poiché il minimum cut considera solo le connessioni esterne al gruppo e non la connettività tra i nodi interni al gruppo.
7.3.4 Normalized cut
Il normalize cut (Shi-Malik, '97) risolve il drawback del minimum cut andando ad introdurre il concetto di volume. Il volume di un gruppo è la somma dei pesi (se il grafo è pesato) degli archi con almeno un endpoint in , quindi Il normalized cut è definito come segue: Tale criterio produce partizioni bilanciate, tuttavia trovare il taglio ottimale è un problema NP-hard, per cui non si andrà a trovare la soluzione esatta, bensì una soluzione approssimata ma certamente più efficiente.
7.3.5 Spectral Graph Partitioning
Sia la matrice di adiacenza del grafo non direzionato (quindi se ). Sia un vettore in con componenti (pensiamolo come etichette/valori di ogni nodo in ).
Eseguendo il prodotto riga-colonna tra ed otterremo un vettore in cui l'-esima componente non è altro che la somma di tutte le etichette dei vicini di . Quindi La spectral graph teory non fa altro che analizzare lo spettro della matrice che rappresenta il grafo . Per spettro si intendono gli autovettori del grafo, ordinati per la magnitudo (forza) dei corrispondenti autovalori :
D-regular graph
Supponiamo che sia un grafo d-regolare, ovvero che tutti i nodi di abbiano grado . Inoltre supponiamo che sia connesso. Quali sono gli autovalori ed autovettori di ?
Inizializziamo tutte le componenti di ad 1 ed osserviamo: Se ogni nodo ha vicini e le etichette valgono tutte 1, allora le componenti del vettore risultante saranno tutte pari a (poiché l'-esima componente non è altro che la somma di tutte le etichette dei vicini di .). Questo vuol dire che: Dove , quindi la coppia e è una autocoppia.
D-regular graph con due componenti
Se è disconnesso ed ha 2 componenti, ognuna -regolare, allora succede che le righe della matrice di adiacenza assumeranno due forme differenti:
- Se appartiene alla componente , avrà 1 in nodi interni a e 0 nei rimanenti
- quindi
- Se appartiene alla componente , avrà 1 in nodi interni a e 0 nei rimanenti
- quindi
In entrambi i casi si ha che . L'intuizione è la seguente: se con due componenti separate i due autovalori sono uguali, allora se esiste qualche arco tra le due componenti, gli autovalori resteranno pressoché uguali.

Inoltre gli autovettori sono ortogonali tra loro, quindi . In un grafo -regolare, il primo autovettore sarà . Essendo che il prodotto scalare è nullo, allora sicuramente il secondo vettore dovrà contenere anche dei valori negativi.
L'intuizione alla base dello spectral clustering consiste nel prendere il secondo autovettore e suddividere i nodi in base al segno: tutti i nodi la cui rispettiva componente è non negativa andranno nel gruppo , tutti gli altri andranno nel gruppo .
Matrice laplaciana
Sia una matrice di adiancenza del grafo , di dimensione . Sotto ipotesi di grafo non direzionato, la matrice di adiacenza è simmetrica, con autovettori reali ed ortogonali.
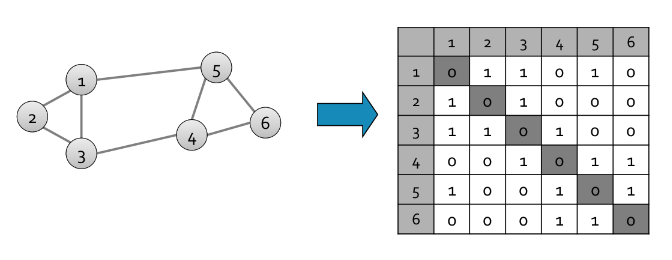
Sia la degree matrix del grafo , ovvero una matrice diagonale di dimensione in cui l'elemento .
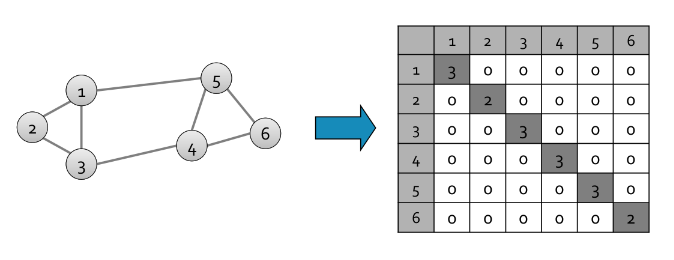
Definiamo la matrice laplaciana del grafo come una matrice simmetrica di dimensione definita come .
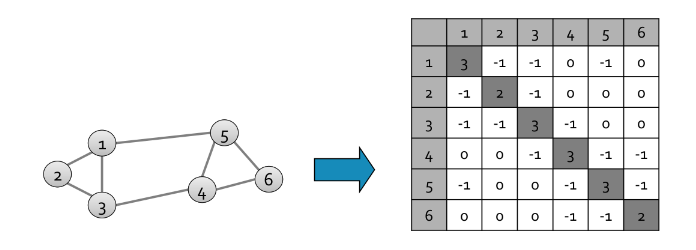
Una autocoppia banale della matrice è data dall'autovettore e dall'autovalore , questo poichè la moltiplicazione riga colonna con un vettore corrisponde a sommare gli elementi della riga e, possiamo osservare, che la somma di ogni riga nella matrice laplaciana è 0. La matrice Laplaciana gode delle seguenti proprietà:
- (a) Ha autovalori reali non negativi
- Ha autovettori reali ed ortogonali
- (b) per ogni autovettore
- (c) È semidefinita positiva ()
- Direzionando casualmente , possiamo porre ovvero la sua matrice di incidenza.
Alcune dimostrazioni:
- (moltiplicazione del vettore per se stesso è )
- sia un autovalore di , dalla ne segue che quindi (dato che è autovettore) (nota che poiché è unitario).
7.3.6 Autocoppia di Fiedler
Diamo per assunto che per una generica matrice simmetrica valga la seguente proprietà: L'autovalore viene chiamato autovalore di Fiedler ed il suo corrispettivo autovettore prende il nome di vettore di Fiedler.
Dato che la matrice laplaciana è una matrice simmetrica, possiamo scrivere che: Focalizziamoci sul prodotto al numeratore: Adesso scomponiamo la matrice laplaciana Dato che per è una matrice diagonale, allora tutti i valori al di fuori della diagonale varranno 0. Inoltre la matrice di adiacenza ha valori diversi da 0 solo se esiste un arco tra i due nodi, quindi riscriviamo l'espressione come segue: Essendo un grafo non direzionato considereremo al secondo membro lo stesso arco 2 volte. Osserviamo che, per ogni arco presente nel grafo, saranno presenti ed dal primo membro, e al secondo membro. Questo sembra essere proprio un quadrato di binomio, quindi riscriviamo: Imponiamo dei vincoli sul vettore :
- (a) sarà un vettore unitario
- (b) sarà ortogonale al primo autovettore
- Quindi
- Ovvero vi saranno sia componenti positive che negative
Quindi scriviamo Tenendo conto dei vincoli imposti (essendo il denominatore pari ad 1 è possibile rimuoverlo dalla minimizzazione). Nella pratica vogliamo assegnar nel vettore dei valori positivi ai nodi di un gruppo e dei valori negativi ai nodi dell'altro gruppo tale che vi siano pochi archi che attraversino lo 0.
Ritornando al taglio ottimale, esprimiamo come un vettore tale che Per ottenere una partizione (sub)ottimale si minimizza l'espressione Tuttavia non è possibile risolvere tale equazione in modo esatto, per cui si rilassa ammettendo valori reali (e non solo -1 ed 1).
Teorema di Rayleigh
Il teorema di Rayleigh enuncia che, per il seguente problema di minimizzazione: Vale che
- , ovvero il minimo di è dato dal secondo più piccolo autovalore del laplaciano .
- , ovvero la soluzione ottimale per è data dal corrispondente autovettore , chiamato vettore di Fiedler.
Approssimazione garantita
Ricordiamo che: se un grafo ha una espansione , allora è garantito che comunque preso un sottoinsieme di nodi il numero di archi uscenti da è maggiore o uguale a .
Supponiamo di avere una partizione in in e dove , possiamo porre l'espansione pari a:
\alpha = \frac{\text{#archi da A a B}}{|A|}
allora possiamo garantire che l'autovalore di Fiedler . L'espansione corrisponde al taglio ottimale applicabile ad un grafo. Tale approssimazione ci dice che ciò che troviamo con lo spectral clustering è al più due volte peggiore dello score ottimale .
Dimostrazione
Sia e , con e = \text{#archi da A a B}. Possiamo scegliere basato su e tale che: Impostiamo Ovviamente la somma di tutte le componenti di è pari a zero, poichè avremo volte e volte , quindi e viene rispettato il vincolo di ortogonalità tra ed il primo autovettore . Riscriviamo: E da qui costruiamo la disequazione
e \left(-\frac 1 a + \frac 1 b \right) \le e \left(\frac 1 a + \frac 1 b \right) \le e \left(\frac 1 a + \frac 1 a \right) = e \left(\frac 2 a \right) = \ = 2 \frac{e}{a} = 2\frac{\text{#archi da A a B}}{|A|} = 2 \alpha
Per transitività abbiamo che .
Un lower bound per (dato per buono) è che , dove è il grado massimo nel grafo.
7.3.7 Spiegazione semplice
Sia un grafo non direzionato e non pesato con nodi, sia la sua matrice di adiacenza. Essendo un grafo indiretto, sarà simmetrica. Definiamo : Sia la matrice dei gradi di , ovvero una matrice diagonale definita come segue: Definiamo adesso la matrice laplaciana del grafo dalla differenza , ovvero: La matrice laplaciana è semidefinita positiva ed ha autovalori reali non negativi. Siano gli autovalori di , ordinati in maniera crescente , e siano i rispettivi autovettori. Gli autovalori rivelano proprietà del grafo non osservabili dalla matrice di adiacenza:
- (a) Se , allora il grafo ha componenti connesse.
- (b) Se il grafo è connesso, allora ed è chiamato autovalore di Fiedler.
- (c) e perché la somma delle righe di risulta 0.
Più alto è l'autovalore di Fiedler, più il grafo è densamente connesso. Nella pratica si prende l'autovettore corrispondente all'autovalore di Fiedler, chiamato vettore di Fiedler e si effettua un bipartizionamento come segue: Per l'osservazione , più piccolo è , migliore è il bipartizionamento. Sia la funzione definita come segue: Per il teorema di Rayleigh sappiamo che e . Inoltre, sia l'espansone del grafo , si può dimostrare che .
7.3.8 Procedura
Nella pratica, lo spectral clustering consiste in tre fasi:
- il preprocessing, dove si calcola la matrice Laplaciana
- la decomposizione, dove si identificano le autocoppie di .
- Il grouping dove si mappano i nodi nei due gruppi in base alle componenti dell'autovettore corrispettivo all'autovalore (es. valori negativi in e valori positivi in ).
7.3.8 K-way Spectral clustering
Possiamo partizionare il grafo in cluster utilizzando varie tecniche, le più utilizzate sono:
- Recursive bi-partitioning: Si applica ricorsivamente la bipartizione e si suddividono i cluster in modo gerarchico (inefficiente, instabile).
- Cluster multiple eigenvector: Si costruisce uno spazio ridotto utilizzando gli autovettori e si effettua il clustering per identificare le comunità.
Usare diversi autovettori aiuta ad approssimare il cut ottimale, sottolinea cluster coesivi e divide i nodi in uno spazio ben separato.
7.4 Sweep
L'algoritmo Sweep utilizza il PageRank per identificare dei cluster densi. Il grafo su cui si opera è spesso molto grande, per cui l'utilizzo di algoritmi di ordine maggiore a quello lineare è sconsigliabile. Lo Sweep ha un tempo proporzionale alla dimensione dei cluster (e non a quella del grafo).
7.4.1 Idea
Prendiamo un nodo seed ed eseguiamo un PageRank personalizzato con teleport set . Se appartiene ad un cluster, allora il random surfer resterà con molta probabilità intrappolato all'interno di esso.
7.4.2 Conduttanza
Prima di parlare dell'algoritmo in sé, è necessario introdurre il concetto di conduttanza. La conduttanza indica la connettività di un gruppo rispetto al resto della rete, relativa alla densità del gruppo. Ovviamente un buon cluster ha una bassa conduttanza. Sia , la conduttanza è definita come segue:
\phi(S) = \frac {\text{#archi da } S \text{ a } (V \setminus S)} {\min(vol(S), 2m-Vol(S))} = \frac{cut(S)}{\min(vol(S), 2m-Vol(S))}
Dove ovviamente e quindi , ed . Utilizzando questo criterio come guida induce a produrre partizionamenti più bilanciati.
7.4.3 Algoritmo
L'algoritmo è descritto nei seguenti passi:
- Scegliere un nodo di interesse
- Eseguire il Personalized-PageRank (PPR) con teleport
- Ordinare i nodi in modo decrescente rispetto allo score PPR
- Quindi si produce una sequenza
Dopodiché si procede con lo sweep:
- Si inizializza
- Per :
- Si calcola la conduttanza per il cluster
Dato che un buon cluster ha una bassa conduttanza, possiamo considerare come buon cluster il cluster che restituisca un minimo locale di .
Calcolo in tempo lineare
La curva di Sweep può essere calcolata in tempo lineare:
- Iteriamo sui nodi
- Manteniamo una tabella hash dei nodi in
- Calcoliamo dove:
- cut(A_{t+1}) = cut(A_{t}) + d_{i+1} - 2\text{#(archi da u_{i+1}A_t})
7.4.4 PageRank approssimato
Ipotizziamo di effettuare un pagerank con teletrasporto a partire dal nodo . Sia un vettore di residui con tutte le componenti nulle tranne la componente . Supponiamo di voler approssimare il vettore che contiene i pagerank score con un vettore inizialmente posto a 0, ammettendo un errore controllato dalla costante . Definiamo l'azione di push:
push(u, r, q):
r' = r
q' = q
# prendiamo (1-beta dal residuo) e cediamolo ad r'(u)
r'(u) = r(u) + (1-beta) * q(u)
# resta q(u)*beta residuo disponibile
# di questo ne teniamo solo la metà
q'(u) = (q(u) * beta) * 0.5
# cediamo l'altra metà al rank dei vicini N(u) di u
for v : (v,u) in E:
residuo_rimanente = 0.5 * ( beta * q(u) ) /
q'(v) = q(v) + ( residuo_rimanente / |N(u)| )
# ritorniamo i vettori aggiornati
return r', q'
Possiamo dare per assunto che il residuo sia tale che: Quindi se è alto vuol dire che nella approssimazione stiamo sottostimando il reale score del nodo . Come facciamo a sapere se è alto? Possiamo ancora una volta dare per assunto che se si verifica allora il residuo è alto. Quando non si verifica più tale condizione per il nodo , allora abbiamo raggiunto una buona approssimazione del suo pagerank score. Quindi definiamo il PageRank approssimato come segue:
ApproxPageRank(S, beta, eps):
r = [0, ..., 0]
q = [0, ..., 1, ..., 0] # asserire il nodo di partenza
while (esiste u : ( q(u) / d(u) >= eps ) :
r, q = push(u, r, q)
return r, q
Questo algoritmo utilizza inoltre il lazy random walk, secondo la quale lo step di aggiornamento è definito come segue: Ovvero con probabilità del % si sta fermi, con la restante ci si muove.
Il pagerank approssimato calcola il personalized pagerank in un tempo pari a , mentre la power iteration richiederebbe un tempo pari a . Si può dimostrare che se esiste un taglio con conduttanda e volume , allora il metodo trova un taglio di conduttanda .
7.5 Motif-Based Clustering
Preso in input un grafo , per ogni tipo di motif (sottografo, graphlet) possibile si vanno a contare le occorrenze del sottofrafo in .
Focalizziamoci su un motif specifico in e prendiamo . Definiamo:
- Motif cut: quanti motif hanno endpoint sia in che fuori da
- Motif volume: quanti endpoint (stub) dei vari motif cadono in
- Motif conduttanza: il rapporto tra il motif cut ed il motif volume
Ovvero abbiamo ri-definito le metriche precedenti, utilizzando i motif anziché gli archi.
Considerato un certo motif , l'algoritmo consiste in un primo passo di preprocessing, in cui si calcola la matrice , dove l'elemento indica il numero di volte in cui l'arco partecipa ad una istanza del motif .
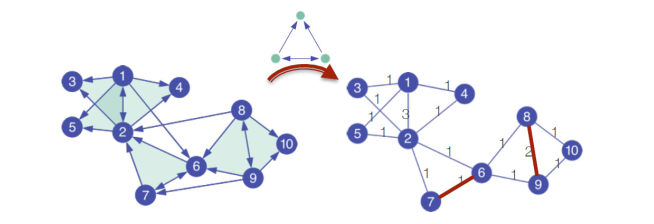
Dopodiché si calcola un approximated PageRank utilizzando la matrice pesata e si procede con lo sweep per andare ad individuare i cluster.
7.6 Louvain - Ottimizzazione della modularità
L'algoritmo di Louvain è un algoritmo di community detection che tenta di ottimizzare la modularità con un approccio greedy e con un running time . Questo algoritmo funziona anche con grafi pesati ed è ampiamente utilizzato per grosse reti.
7.6.1 Riformulare la modularità
Considerando il configuration model come modello nullo, dato un grafo ed un partizionamento , abbiamo definito la modularità come segue:
Essendo che non si considerano mai archi con endpoint su cluster differenti, possiamo andare a riformulare la modularità utilizzando la funzione Delta di Dirac . Supponiamo che indichi il cluster a cui il nodo è associato, allora:
Quindi riscriviamo la modularità:
7.6.2 Idea generale
L'algoritmo si divide in due fasi:
- La prima fase consiste nell'esaminare i cluster a coppie e spostare i nodi da un cluster ad un altro se e solo se si ha un incremento della modularità.
- La seconda fase aggrega i cluster in supernodi per costruire una nuova rete.
Si ritorna quindi alla prima fase, fino a che non si ha un supernodo che rappresenti l'intera rete.
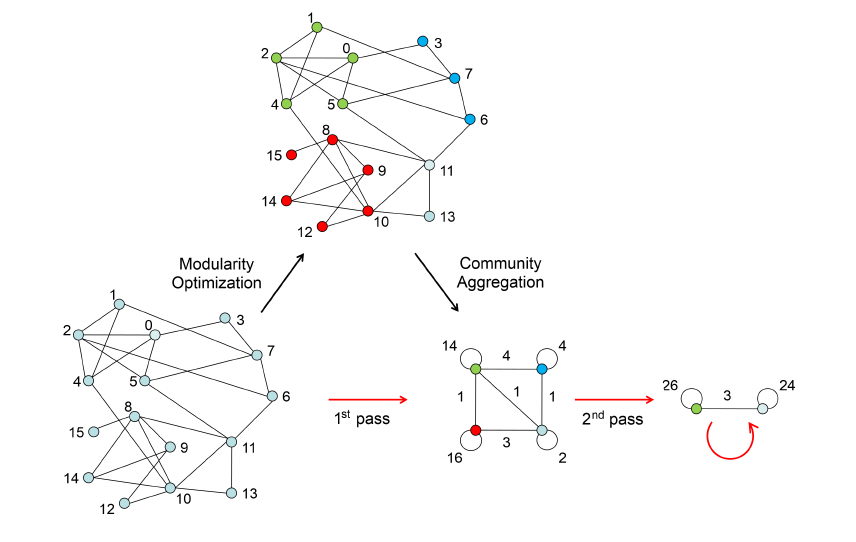
7.6.3 Prima fase - Partizionamento
All'inizio dell'algoritmo ogni nodo verrà inserito in un cluster distinto. Dopodiché, per ogni nodo l'algoritmo effettuerà due calcoli:
- Si calcola la modularità quando si inserisce nella comunità di un vicino
- Si sposta nella comunità del nodo che da il maggiore guadagno .
La fase 1 finisce quando non ci sono movimenti che possano aumentare il guadagno. L'ouput dell'algoritmo dipende dall'ordine in cui i nodi sono processati. La fase finisce con un massimo locale della modularità.
Calcolo della modularità su singolo cluster
A cosa corrisponde quando muoviamo il nodo nella comunità ? Supponiamo di voler muovere il nodo dalla comunità alla comunità , quindi vogliamo calcolare Dove corrisponde al gain che si ha quando si toglie da e si forma una ulteriore comunità formata solamente da , mentre è il gain che si ha spostando all'interno di .
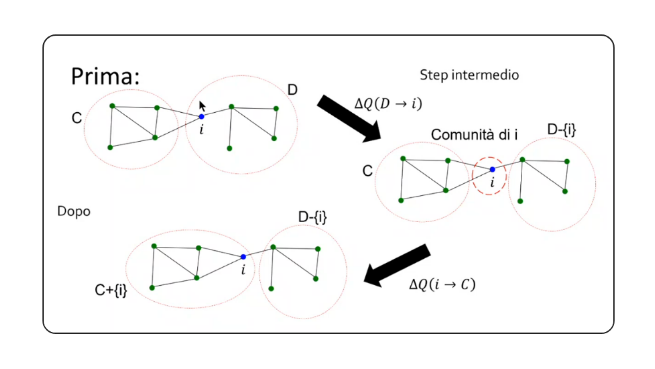
Definiamo la modularità per un singolo cluster come: Definiamo: Ovvero la somma degli archi (o dei pesi degli archi) tra nodi all'interno del cluster .
Definiamo: Ovvero la somma degli archi (o dei pesi degli archi) di ogni nodo nel cluster .
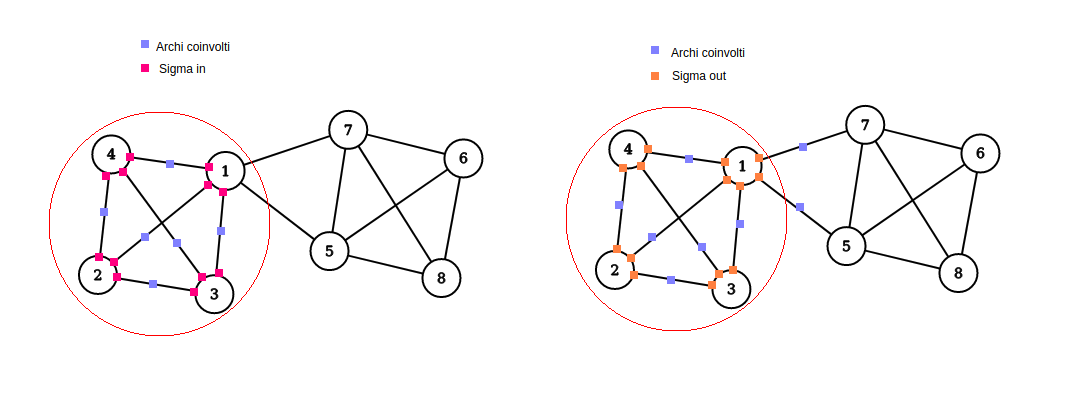
Riscriviamo come segue: Quindi
Derivare
Abbiamo considerato il nodo , distaccato dal cluster , come un cluster a sé stante. Dobbiamo calcolare . Prima di tutto, definiamo le quantità:
- che equivale alla somma degli archi (o dei pesi degli archi) tra ed il cluster .
- che equivale alla somma degli archi (o pesi degli archi) del nodo , ovvero il suo grado.
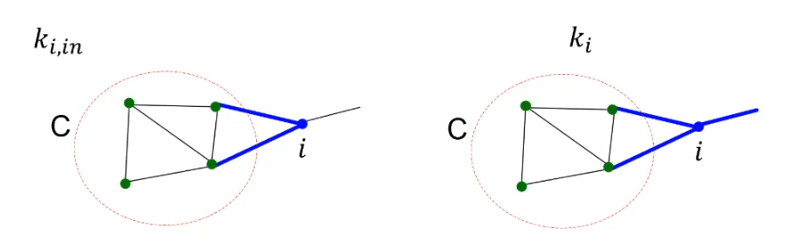
Definiamo la modularità prima del merging di su : E la modularità dopo il merging: Allora possiamo dire che Con lo stesso principio si calcola .
7.6.4 Seconda fase - Collasso
Tutte le community ottenute nella prima fase sono contratte in super-nodi, e una nuova rete viene creata di conseguenza:
- I super-nodi sono connessi se esiste almeno un arco che connette le due community
- Il peso dell'arco tra due super-nodi è pari alla somma dei pesi degli archi dei nodi che connettono le community
- I super-nodi hanno dei cappi con peso pari alla somma dei pesi degli archi interni.
Dopodiché viene ripetuta la prima fase utilizzando la nuova rete.
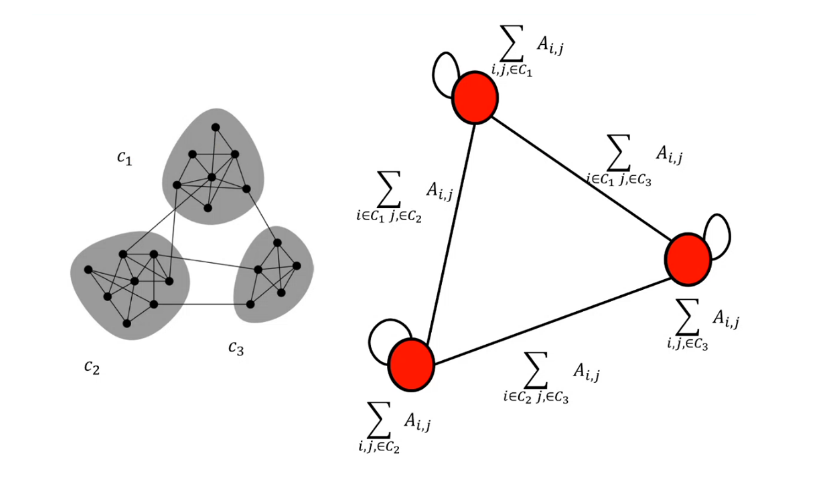
7.7 Trawling - Analisi di grandi grafi
L'algoritmo Trawling permette di identificare delle piccole comunità all'interno del web. Utilizzando questo algoritmo, è possibile identificare i topic comuni tra le pagine web: pagine che parlano dello stesso topic sono collegate tra loro con alta probabilità.
7.7.1 Idea
Supponiamo di disporre in due layer differenti (1, 2) gli stessi nodi di un grafo . Colleghiamo il nodo dal layer 1 con tutti i suoi vicini nel grafo sul layer 2. Due nodi e che stanno all'interno della stessa comunità, molto probabilmente avranno tanti vicini in comune.
7.7.2 Definire il problema
Si vogliono enumerare i sottografi completi bipartiti , dove con indichiamo il numero di nodi a sinistra (layer 1), dove ognuno di essi si collega agli stessi nodi sulla destra (layer 2).
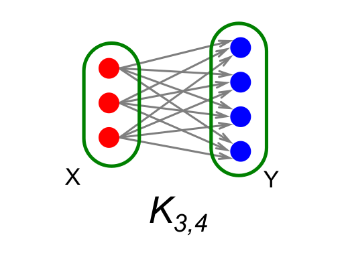
7.7.3 Frequent Itemset Enumeration
Utilizziamo le tecniche del Market Basket Analysis (MBA) per risolvere il problema. Definiamo un universo di item. Definiamo i basket come sottoinsiemi di , . Definiamo il supporto come un threshold di frequenza. Vogliamo trovare tutti i sottinsiemi tale che in almeno insiemi , ovvero gli item in sono stati "acquistati" insieme almeno volte.
Colleghiamo il task del MBA al grafo bipartito: se il nodo ha come vicini i nodi , allora definiamo il basket . Il nostro sarà un insieme di cardinalità che si presenta in insiemi (ovvero avremo nodi con gli stessi vicini). Cercare vuol dire cercare un insieme con una frequenza minima e di cardinalità . Definito il problema, basta utilizzare uno tra gli algoritmi di MBA per trovare gli itemset frequenti.
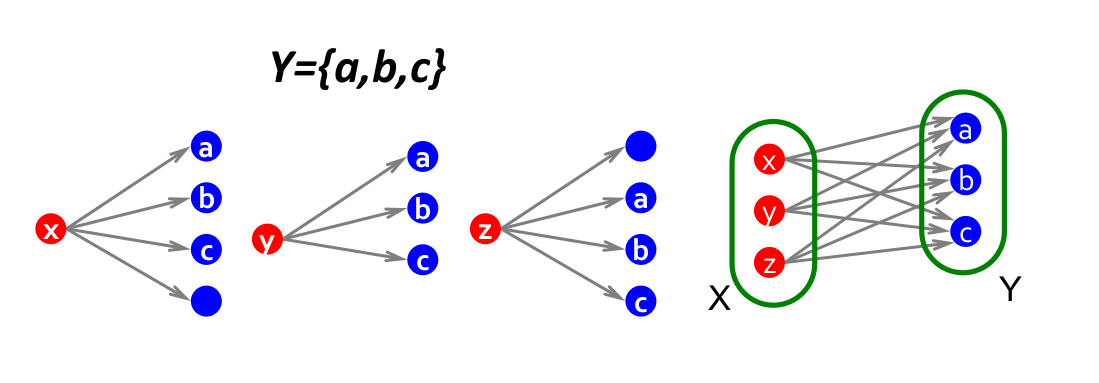
Le comunità risultati si sovrappongono: un nodo potrebbe stare in più comunità contemporaneamente (overlapping).